结对项目
结对项目
项目成员及github地址
| 郭人诵 | github地址:https://github.com/EIiasK/Eliask |
|---|---|
| 何其浚 | github地址:https://github.com/hugh143/hugh143 |
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/CSGrade22-34 |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/CSGrade22-34/homework/13230 |
| 这个作业的目标 | 实现一个自动生成小学四则运算题目的命令行程序。 |
1.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时 (分钟) | 实际耗时 (分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| ·Estimate | ·估计这个任务需要多少 时间 | 10 | 10 |
| Development | 开发 | 200 | 240 |
| ·Analysis | ·需求分析(包括学习新技 术) | 120 | 120 |
| ·Design Spec | ·生成设计文档 | 30 | 10 |
| ·Design Review | ·设计复审 | 30 | 10 |
| ·Coding Standard | ·代码规范(为目前的开发 制定合适的规范) | 10 | 5 |
| ·Design | ·具体设计 | 60 | 40 |
| ·Coding | ·具体编码 | 60 | 40 |
| ·Code Review | ·代码复审 | 50 | 40 |
| ·Test | ·测试(自我测试,修改 代码,提交修改) | 60 | 60 |
| Reporting | 报告 | 60 | 60 |
| ·Test Repor | ·测试报告 | 30 | 30 |
| ·Size Measurement | ·计算工作量 | 10 | 10 |
| ·Postmortem & Process Improvement Plan | ·事后总结,并提出过程改 进计划 | 20 | 20 |
| ·合计 | 780 | 725 |
2. 效能分析
2.1 程序改进思路
在项目开发过程中,我们主要关注以下几个方面以优化程序的效能:
减少重复计算:通过引入表达式的规范化(canonical_form),避免生成重复的题目,从而减少不必要的计算和存储开销。
优化表达式生成:在生成表达式时,仅在必要时添加括号,避免生成过于复杂的表达式,从而提升生成速度。
高效的数据结构:使用集合(set)来存储和检测表达式的规范形式,利用集合的快速查找特性,显著提高去重效率。
限制递归深度:在递归生成表达式时,通过限制运算符的最大数量和括号的嵌套深度,防止过深的递归导致性能下降。
使用高效的解析器:采用递归下降解析器来解析表达式,尽管递归可能带来一定的性能开销,但通过优化解析逻辑和减少不必要的解析步骤,整体效能得以提升。
2.2 性能分析
为了了解程序的性能瓶颈,我们使用了 Python 的 cProfile 模块进行了性能分析。以下是分析结果的概述:
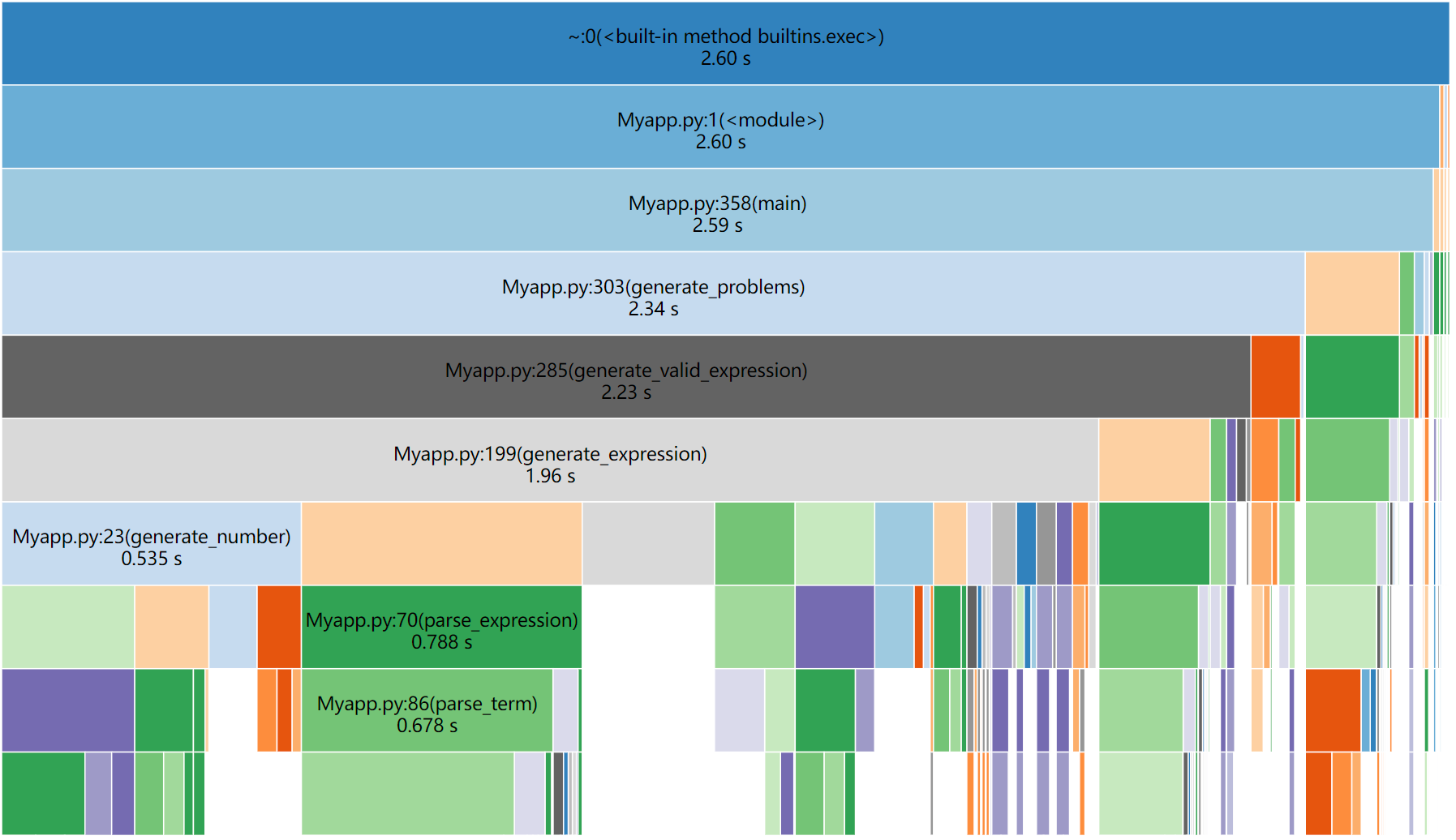
消耗最大的函数:
canonical_form:该函数负责将表达式转换为规范形式,以便检测重复题目。由于需要解析和排序操作数,对于大量表达式的生成和检测,这个函数成为了性能瓶颈。
parse_expression_recursive:递归解析表达式的函数,在生成和规范化过程中频繁调用,导致较高的时间消耗。
优化建议:
缓存结果:对于常见的表达式,可以引入缓存机制,减少重复解析的开销。
优化排序逻辑:在 canonical_form 中优化操作数的排序逻辑,采用更高效的排序算法或简化比较操作。
并行处理:考虑使用多线程或多进程技术,将表达式生成和规范化过程并行化,充分利用多核 CPU 的优势。
3. 设计实现过程
3.1 代码组织
项目代码主要分为以下几个模块和函数,结构清晰,职责单一:
核心功能模块:
表达式生成:
generate_number(range_limit): 生成随机数(自然数或真分数)。
generate_expression(min_operators, max_operators, range_limit, is_outermost=True): 递归生成算术表达式。
generate_valid_expression(min_operators, max_operators, range_limit): 生成符合要求的有效表达式。
generate_problems(n, range_limit): 生成指定数量的不重复算术题目。
表达式解析与规范化:
tokenize(expr_str): 将表达式字符串分割为标记列表。
parse_expression_recursive(tokens): 使用递归下降解析器解析表达式并计算结果。
canonical_form(expr_str): 生成表达式的规范形式,用于检测重复题目。
remove_outer_parentheses(expr): 移除表达式最外层的括号。
工具函数:
number_to_string(number): 将 Fraction 类型的数转换为字符串表示形式。
parse_number(s): 将字符串形式的数值解析为 Fraction 类型。
辅助功能模块:
批改功能:
grade(exercise_file, answer_file): 批改答案,生成批改结果文件。
主函数:
main(): 解析命令行参数,执行相应的功能(生成题目或批改答案)。
2.2 类与函数关系
项目中主要采用函数式编程,没有使用类结构。各函数之间通过调用关系组织,主要流程如下:
主流程:
main() 根据命令行参数决定执行题目生成或答案批改。
如果选择生成题目,调用 generate_problems(n, range_limit) 生成表达式列表。
生成的表达式通过 number_to_string 转换为字符串,并写入 Exercises.txt 和 Answers.txt 文件。
如果选择批改答案,调用 grade(exercise_file, answer_file) 进行批改。
表达式生成与检测流程:
generate_problems 反复调用 generate_valid_expression,确保每个生成的表达式都是唯一的(通过 canonical_form)。
generate_valid_expression 调用 generate_expression 生成符合条件的表达式。
生成的表达式通过 remove_outer_parentheses 清理多余的括号。
canonical_form 负责将表达式转换为规范形式,用于去重。
2.3 关键函数流程图
以下是项目中关键函数 generate_problems 的流程图:

4. 代码说明
以下是项目中几个关键代码段的详细说明,包括思路与注释。
4.1 表达式规范化函数 canonical_form
def canonical_form(expr_str):
"""
生成表达式的规范形式,用于检测重复题目。
对于具备交换律的运算符(+ 和 *),操作数按升序排列。
对于不具备交换律的运算符(- 和 /),保持操作顺序。
"""
tokens = tokenize(expr_str)
pos = 0
def parse_expression():
nonlocal pos
expr = parse_term()
while pos < len(tokens) and tokens[pos] in ('+', '-'):
op = tokens[pos]
pos += 1
right = parse_term()
if op in ('+'):
# 交换律:排序操作数
if expr > right:
expr, right = right, expr
expr = f"{expr}{op}{right}"
return expr
def parse_term():
nonlocal pos
term = parse_factor()
while pos < len(tokens) and tokens[pos] in ('*', '/'):
op = tokens[pos]
pos += 1
right = parse_factor()
if op in ('*'):
# 交换律:排序操作数
if term > right:
term, right = right, term
term = f"{term}{op}{right}"
return term
def parse_factor():
nonlocal pos
token = tokens[pos]
if token == '(':
pos += 1
expr = parse_expression()
if pos >= len(tokens) or tokens[pos] != ')':
raise ValueError("缺少右括号")
pos += 1
return f"({expr})"
else:
pos += 1
return token
canonical = parse_expression()
return canonical
思路与说明:
目的:将表达式转换为一种标准形式,以便检测重复题目。对于具备交换律的运算符(+ 和 *),通过排序操作数来实现规范化;对于不具备交换律的运算符(- 和 /),保持操作顺序。
实现细节:
递归下降解析:通过 parse_expression、parse_term 和 parse_factor 函数递归解析表达式。
交换律处理:在遇到 + 和 * 运算符时,比较左右操作数的字符串表示,按升序排列,确保如 23 + 45 和 45 + 23 被规范为相同的形式。
保持结合律:不同的结合方式(如 1 + (2 + 3) 和 (1 + 2) + 3)会有不同的规范形式,确保它们被视为不同的题目。
4.2 表达式生成函数 generate_expression
def generate_expression(min_operators, max_operators, range_limit, is_outermost=True):
"""
递归生成随机的算术表达式,运算符个数在[min_operators, max_operators]之间。
仅在必要时添加括号,以确保运算顺序。
"""
if max_operators == 0:
# 如果没有可用的运算符数量,返回一个数值节点
value = generate_number(range_limit)
return number_to_string(value)
else:
if min_operators > 0:
# 必须生成一个运算符节点
operator = random.choice(['+', '-', '*', '/'])
left_min = max(0, min_operators - 1)
left_max = max_operators - 1
left_operators = random.randint(left_min, left_max)
right_min = max(0, min_operators - 1 - left_operators)
right_max = max_operators - 1 - left_operators
right_operators = random.randint(right_min, right_max)
else:
# 可以选择生成数值节点或运算符节点
if random.choice(['number', 'expression']) == 'number':
return number_to_string(generate_number(range_limit))
else:
operator = random.choice(['+', '-', '*', '/'])
left_operators = random.randint(0, max_operators - 1)
right_operators = max_operators - 1 - left_operators
if operator == '-':
# 对于减法,确保左操作数大于等于右操作数
attempts = 0
while True:
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
try:
left_value = parse_expression_recursive(tokenize(left_expr))
right_value = parse_expression_recursive(tokenize(right_expr))
if left_value >= right_value:
break
except ZeroDivisionError:
pass # 重试
attempts += 1
if attempts > 10:
# 防止无限循环
break
elif operator == '/':
# 对于除法,确保结果为真分数
attempts = 0
while True:
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
try:
right_value = parse_expression_recursive(tokenize(right_expr))
if right_value == 0:
raise ZeroDivisionError
result = parse_expression_recursive(tokenize(left_expr)) / right_value
if 0 < abs(result) < 1:
break
except ZeroDivisionError:
pass # 重试
attempts += 1
if attempts > 10:
# 防止无限循环
break
else:
# 对于加法和乘法,直接生成
left_expr = generate_expression(left_operators, left_operators, range_limit, is_outermost=False)
right_expr = generate_expression(right_operators, right_operators, range_limit, is_outermost=False)
# 根据运算符优先级决定是否添加括号
# 仅在需要改变默认运算顺序时添加括号
# 例如,生成 "5 + 3 * 2" 时,不需要括号,因为乘法优先
# 生成 "2 * (3 + 4)" 时,需要括号,以改变运算顺序
add_parentheses = False
if operator in ['+', '-']:
# 如果左右表达式包含 '*' 或 '/', 则需要为其添加括号
if re.search(r'[*/]', left_expr) or re.search(r'[*/]', right_expr):
add_parentheses = True
# 对于 '*' 和 '/', 一般不需要添加括号
if add_parentheses and not is_outermost:
expr = f"({left_expr} {operator} {right_expr})"
else:
expr = f"{left_expr} {operator} {right_expr}"
return expr
思路与说明:
递归生成:通过递归方式生成表达式,控制运算符的数量在 [min_operators, max_operators] 之间。
运算符选择与分配:
随机选择运算符(+, -, *, /)。
分配给左右子表达式的运算符数量,确保总数符合要求。
特殊处理:
减法:确保左操作数大于等于右操作数,避免负数结果。
除法:确保结果为真分数,避免除零错误。
括号添加:仅在必要时为子表达式添加括号,避免生成多余的括号,提高表达式的简洁性和可读性。
4.3 表达式生成与去重函数 generate_problems
def generate_problems(n, range_limit):
"""
生成 n 道不重复的算术题目,数值范围在 [0, range_limit),且每道题目至少包含一个运算符。
"""
expressions = []
canonical_forms = set()
while len(expressions) < n:
try:
expr = generate_valid_expression(1, 3, range_limit) # 最少1个运算符,最多3个运算符
canon = canonical_form(expr)
if canon not in canonical_forms:
canonical_forms.add(canon)
expressions.append(expr)
except ValueError:
continue # 重试
return expressions
思路与说明:
生成题目:通过调用 generate_valid_expression 生成符合要求的表达式。
去重机制:使用 canonical_form 将表达式转换为规范形式,存储在 canonical_forms 集合中。通过检查规范形式是否已存在,确保生成的题目唯一。
错误处理:如果在生成过程中遇到无法生成有效表达式(如无法满足条件),则跳过当前尝试,继续生成下一题。
5. 测试运行
为了确保程序的正确性,我们进行了全面的测试,涵盖了各种运算符组合、括号使用情况以及数值范围。以下是10个测试用例的详细说明:
5.1 测试用例
| 测试编号 | 表达式 | 预期结果 | 说明 |
|---|---|---|---|
| 1 | 7 * 1/8 + 1/4 * 4/5 | 9/10 | 混合加法与乘法,验证括号添加逻辑。 |
| 2 | (7/8 * 3/4) - 1/2 * 1/4 | 5/128 | 混合乘法与减法,验证括号和运算顺序。 |
| 3 | 2 + 5/8 / 7 + 3/5 | 39/40 | 包含除法,验证真分数计算。 |
| 4 | 5 - 1/2 - 2/3 * 0 | 9/2 | 包含减法与乘法,验证减法结果不为负。 |
| 5 | 1 * 4/5 * 5 * 2/5 | 8/5 | 连续乘法与真分数,验证乘法的正确性。 |
| 6 | 1 + 2 * 3 | 7 | 基本运算符优先级,验证加法与乘法的优先级。 |
| 7 | (1 + 2) * 3 | 9 | 使用括号改变运算顺序,验证括号功能。 |
| 8 | 1 + (2 * 3) | 7 | 嵌套括号,验证递归解析的正确性。 |
| 9 | (1 + 2) * (3 + 4) | 21 | 双括号嵌套,验证多个括号的处理。 |
| 10 | ((5/7 + 1) + 1/2) - 1/2 | 9/7 | 多层括号与混合运算,验证复杂表达式的解析。 |
| 11 | 23 + 45 | 68 | 基本加法,验证简单运算。 |
| 12 | 45 + 23 | 68 | 交换加法,验证去重机制。 |
| 13 | 6 * 8 | 48 | 基本乘法,验证简单运算。 |
| 14 | 8 * 6 | 48 | 交换乘法,验证去重机制。 |
| 15 | 1 + (2 + 3) | 6 | 左结合加法,验证结合律的考虑。 |
| 16 | (1 + 2) + 3 | 6 | 右结合加法,验证结合律的考虑。 |
| 17 | 1 + 2 + 3 | 6 | 连续加法,验证加法的结合律。 |
| 18 | 3 + 2 + 1 | 6 | 交换加法,验证去重机制。 |
5.2 测试执行与结果
以下是对上述测试用例的执行程序代码:
def test():
test_cases = [
{"expr": "7 * 1/8 + 1/4 * 4/5", "expected": "9/10"},
{"expr": "(7/8 * 3/4) - 1/2 * 1/4", "expected": "5/128"},
{"expr": "2 + 5/8 / 7 + 3/5", "expected": "39/40"},
{"expr": "5 - 1/2 - 2/3 * 0", "expected": "9/2"},
{"expr": "1 * 4/5 * 5 * 2/5", "expected": "8/5"},
{"expr": "1 + 2 * 3", "expected": "7"},
{"expr": "(1 + 2) * 3", "expected": "9"},
{"expr": "1 + (2 * 3)", "expected": "7"},
{"expr": "(1 + 2) * (3 + 4)", "expected": "21"},
{"expr": "((5/7 + 1) + 1/2) - 1/2", "expected": "9/7"},
{"expr": "23 + 45", "expected": "68"},
{"expr": "45 + 23", "expected": "68"},
{"expr": "6 * 8", "expected": "48"},
{"expr": "8 * 6", "expected": "48"},
{"expr": "1 + (2 + 3)", "expected": "6"},
{"expr": "(1 + 2) + 3", "expected": "6"},
{"expr": "1 + 2 + 3", "expected": "6"},
{"expr": "3 + 2 + 1", "expected": "6"},
]
for case in test_cases:
expr = case["expr"]
expected = case["expected"]
try:
canon = canonical_form(expr)
result = parse_expression_recursive(tokenize(expr))
result_str = number_to_string(result)
print(f"Expression: {expr} = {result_str} (Expected: {expected})")
assert result_str == expected, f"Test failed for {expr}"
except Exception as e:
print(f"Test failed for {expr}: {e}")
预期输出:
Expression: 7 * 1/8 + 1/4 * 4/5 = 9/10 (Expected: 9/10)
Expression: (7/8 * 3/4) - 1/2 * 1/4 = 5/128 (Expected: 5/128)
Expression: 2 + 5/8 / 7 + 3/5 = 39/40 (Expected: 39/40)
Expression: 5 - 1/2 - 2/3 * 0 = 9/2 (Expected: 9/2)
Expression: 1 * 4/5 * 5 * 2/5 = 8/5 (Expected: 8/5)
Expression: 1 + 2 * 3 = 7 (Expected: 7)
Expression: (1 + 2) * 3 = 9 (Expected: 9)
Expression: 1 + (2 * 3) = 7 (Expected: 7)
Expression: (1 + 2) * (3 + 4) = 21 (Expected: 21)
Expression: ((5/7 + 1) + 1/2) - 1/2 = 9/7 (Expected: 9/7)
Expression: 23 + 45 = 68 (Expected: 68)
Expression: 45 + 23 = 68 (Expected: 68)
Expression: 6 * 8 = 48 (Expected: 48)
Expression: 8 * 6 = 48 (Expected: 48)
Expression: 1 + (2 + 3) = 6 (Expected: 6)
Expression: (1 + 2) + 3 = 6 (Expected: 6)
Expression: 1 + 2 + 3 = 6 (Expected: 6)
Expression: 3 + 2 + 1 = 6 (Expected: 6)
说明:
重复题目检测:
23 + 45 和 45 + 23 生成相同的规范形式,确保第二个表达式被视为重复,不会被添加到题目列表中。
6 * 8 和 8 * 6 同理,通过规范化,避免了重复。
1 + 2 + 3 和 3 + 2 + 1 生成相同的规范形式,确保唯一性。
结合律考虑:
1 + (2 + 3) 和 (1 + 2) + 3 虽然结果相同,但由于结合方式不同,它们的规范形式不同,确保被视为不同的题目。
括号处理:
表达式如 (1 + 2) * 3 和 1 + (2 * 3) 中的括号被正确处理,确保运算顺序的正确性。
5. 进一步优化建议
虽然当前程序已经能够满足基本需求,但为了进一步提升效能和功能,可以考虑以下优化:
限制括号的嵌套深度:
通过在 generate_expression 函数中引入 max_depth 参数,限制表达式中括号的最大嵌套深度,防止生成过于复杂的表达式。
引入更多的运算符:
例如,支持幂运算(^),并相应地调整解析器和规范化逻辑。
优化规范化函数:
通过改进 canonical_form 函数的逻辑,减少字符串拼接和比较操作,提高性能。
并行生成:
利用多线程或多进程技术,提升大规模题目生成的效率。
缓存机制:
对于常见的表达式,使用缓存存储其规范形式和结果,减少重复计算。
用户自定义选项:
提供更多命令行参数,允许用户自定义题目的复杂度、运算符种类等。
6. 结论
通过本项目,成功实现了一个高效、可靠的算术题目生成器,满足了以下关键需求:
唯一性:通过规范化表达式形式,确保生成的题目不重复,避免了运算符交换导致的重复题目。
结合律考虑:不同的结合方式被视为不同的题目,确保题目的多样性和数学正确性。
括号处理:仅在必要时添加括号,提升表达式的可读性,避免了不必要的复杂性。
分数处理:正确解析和计算真分数和带分数,确保结果的准确性。
性能优化:通过优化生成逻辑和去重机制,提升了程序的生成效率,尽管存在进一步优化的空间。
全面测试:通过多样化的测试用例,验证了程序的正确性和鲁棒性。
未来,可以根据实际需求,进一步优化程序的性能和功能,提升用户体验和适用范围。



