支持向量机

 

一、模型概念

支持向量机的模型基本模型是建立在特征空间上的最大间隔线性分类器，通过使用核技巧，可以使它成为非线性分类器。

当训练数据线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机；当训练数据近似线性可分时，通过软间隔最大化，学习一个线性分类器，即软间隔支持向量机；当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

支持向量机的几何意义很直观，用分离超平面分隔线性可分和近似线性可分的数据集（可对每个线性不可分点设置一定的缓冲量，这个缓冲量也会进入最后的最优化目标函数里面），保证分隔的同时，最大化分隔间距。

 

二、优化目标函数

所以其优化目标函数其实也很直观，就是最大化所有类别点到分隔超平面的距离和。其实理解起来就是让类别点尽量远离分类的‘临界’超平面，远离这划清界限的模糊地带，让分类的‘显著程度’高，从而推动分隔超平面远离自己，各类别的样本都推着分隔超平面，就将它挤压到一个特定的位置，即最优解。只是目标函数优化过程中会发现，目标函数的最优值只由离分隔平面最近的一些向量点决定，这也是模型为什么叫支持向量机的原因。

其中，在我理解的时候，觉得有一个难理解的点，分隔超平面到间隔边界距离（其实是函数间隔，实际距离应该是几何间隔）为什么就为1？其实只是认为选定的一个规范化标准而已，取几何间隔为1.

 

而其最终的优化目标函数如下：

 

对于近似线性可分的问题，需要给每个样本点一个松弛变量，也就是一个缓冲，

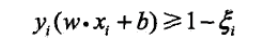
从而其优化目标函数变为：

 

 

 

三、对偶问题

 而实际对支持向量机的目标函数优化，并不是直接对其优化，而是转化成其对偶问题优化。

 

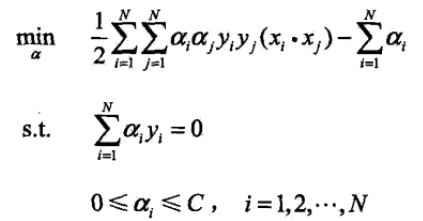
这样的优点是：

1、对偶问题一般相对更简单，对偶问题一定是凸问题（对偶函数是拉格朗日函数的相对乘子变量的逐点下确界，对偶函数必然是凹函数，而求其最大化问题，必然为凸问题），同时也因为普遍的设计变量相对于约束条件更多，对偶反转之后，优化变量变少；另外，某些时候对偶变量具有一定的实际意义。

2、在支持向量机中，对偶问题带来最大优点是，对偶问题目标函数具有变量的內积形式，用非线性內积形式对变量內积形式的替换，可以方便的对线性空间进行某种扭曲，从而实现非线性的分隔问题。特别的，用核函数来替换，甚至不用考虑具体的非线性扭曲的变换形式，只考虑內积变换的结果就可以。

 

 

四、核函数

如下图非线性可分问题

 

 

 

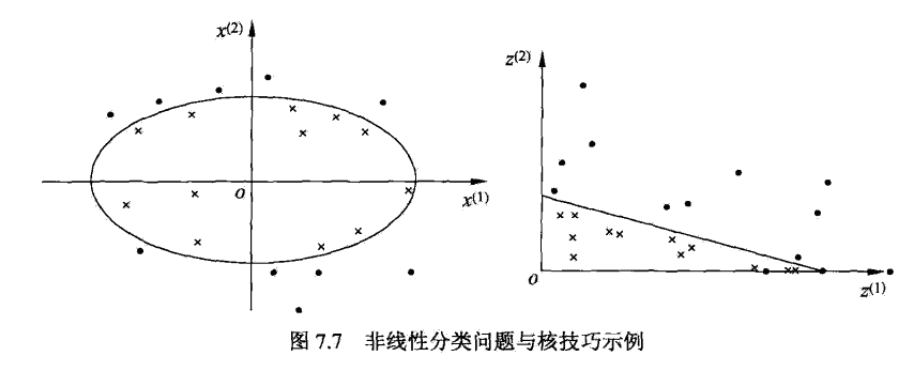
常用的核函数形式有：

Gauss径向基函数则是局部性强的核函数，其外推能力随着参数σ的增大而减弱。

这个核会将原始空间映射为无穷维空间。不过，如果 σ 选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果 σ 选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数σ ，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

 

在吴恩达的课上，也曾经给出过一系列的选择核函数的方法：

• 如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
• 如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
• 如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

 

五、算法优化SMO（sequential minimal optimization）

支持向量机要解决的凸二次规划问题，当样本量很大时，会变得不可用。

 

 SMO算法则采用了一种启发式的方法。它每次只优化两个变量，将其他的变量都视为常数。由于∑i=1mαiyi=0.假如将α3,α4,...,αm固定，那么α1,α2之间的关系也确定了。这样SMO算法将一个复杂的优化算法转化为一个比较简单的两变量优化问题。