解码器 | 基于 Transformers 的编码器-解码器模型
基于 transformer 的编码器-解码器模型是 表征学习 和 模型架构 这两个领域多年研究成果的结晶。本文简要介绍了神经编码器-解码器模型的历史,更多背景知识,建议读者阅读由 Sebastion Ruder 撰写的这篇精彩 博文。此外,建议读者对 自注意力 (self-attention) 架构 有一个基本了解,可以阅读 Jay Alammar 的 这篇博文 复习一下原始 transformer 模型。
本文分 4 个部分:
- 背景 - 简要回顾了神经编码器-解码器模型的历史,重点关注基于 RNN 的模型。
- 编码器-解码器 - 阐述基于 transformer 的编码器-解码器模型,并阐述如何使用该模型进行推理。
- 编码器 - 阐述模型的编码器部分。
- 解码器 - 阐述模型的解码器部分。
每个部分都建立在前一部分的基础上,但也可以单独阅读。这篇分享是最后一部分 解码器。
解码器
如 编码器-解码器 部分所述, 基于 transformer 的解码器定义了给定上下文编码序列条件下目标序列的条件概率分布:
根据贝叶斯法则,在给定上下文编码序列和每个目标变量的所有前驱目标向量的条件下,可将上述分布分解为每个目标向量的条件分布的乘积:
我们首先了解一下基于 transformer 的解码器如何定义概率分布。基于 transformer 的解码器由很多 解码器模块 堆叠而成,最后再加一个线性层 (即 “LM 头”)。这些解码器模块的堆叠将上下文相关的编码序列 \(\mathbf{\overline{X}}_{1:n}\) 和每个目标向量的前驱输入 \(\mathbf{Y}_{0:i-1}\) (这里 \(\mathbf{y}_0\) 为 BOS) 映射为目标向量的编码序列 \(\mathbf{\overline{Y} }_{0:i-1}\)。然后,“LM 头”将目标向量的编码序列 \(\mathbf{\overline{Y}}_{0:i-1}\) 映射到 logit 向量序列 \(\mathbf {L}_{1:n} = \mathbf{l}_1, \ldots, \mathbf{l}_n\), 而每个 logit 向量\(\mathbf{l}_i\) 的维度即为词表的词汇量。这样,对于每个 \(i \in {1, \ldots, n}\),其在整个词汇表上的概率分布可以通过对 \(\mathbf{l}_i\) 取 softmax 获得。公式如下:
“LM 头” 即为词嵌入矩阵的转置, 即 \(\mathbf{W}_{\text{emb}}^{\intercal} = \left[\mathbf{ y}^1, \ldots, \mathbf{y}^{\text{vocab}}\right]^{T}\) \({}^1\)。直观上来讲,这意味着对于所有 \(i \in {0, \ldots, n - 1}\) “LM 头” 层会将 \(\mathbf{\overline{y }}_i\) 与词汇表 \(\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}\) 中的所有词嵌入一一比较,输出的 logit 向量 \(\mathbf{l}_{i+1}\) 即表示 \(\mathbf{\overline{y }}_i\) 与每个词嵌入之间的相似度。Softmax 操作只是将相似度转换为概率分布。对于每个 \(i \in {1, \ldots, n}\),以下等式成立:
总结一下,为了对目标向量序列 \(\mathbf{Y}_{1: m}\) 的条件分布建模,先在目标向量 \(\mathbf{Y}_{1: m-1}\) 前面加上特殊的 \(\text{BOS}\) 向量 ( 即 \(\mathbf{y}_0\)),并将其与上下文相关的编码序列 \(\mathbf{\overline{X}}_{1:n}\) 一起映射到 logit 向量序列 \(\mathbf{L}_{1:m}\)。然后,使用 softmax 操作将每个 logit 目标向量 \(\mathbf{l}_i\) 转换为目标向量 \(\mathbf{y}_i\) 的条件概率分布。最后,将所有目标向量的条件概率 \(\mathbf{y}_1, \ldots, \mathbf{y}_m\) 相乘得到完整目标向量序列的条件概率:
与基于 transformer 的编码器不同,在基于 transformer 的解码器中,其输出向量 \(\mathbf{\overline{y}}_{i-1}\) 应该能很好地表征 下一个 目标向量 (即 \(\mathbf{y}_i\)),而不是输入向量本身 (即 \(\mathbf{y}_{i-1}\))。此外,输出向量 \(\mathbf{\overline{y}}_{i-1}\) 应基于编码器的整个输出序列 \(\mathbf{\overline{X}}_{1:n}\)。为了满足这些要求,每个解码器块都包含一个 单向自注意层,紧接着是一个 交叉注意层,最后是两个前馈层\({}^2\)。单向自注意层将其每个输入向量 \(\mathbf{y'}_j\) 仅与其前驱输入向量 \(\mathbf{y'}_i\) (其中 \(i \le j\),且 \(j \in {1, \ldots, n}\)) 相关联,来模拟下一个目标向量的概率分布。交叉注意层将其每个输入向量 \(\mathbf{y''}_j\) 与编码器输出的所有向量 \(\mathbf{\overline{X}}_{1:n}\) 相关联,来根据编码器输入预测下一个目标向量的概率分布。
好,我们仍以英语到德语翻译为例可视化一下 基于 transformer 的解码器。
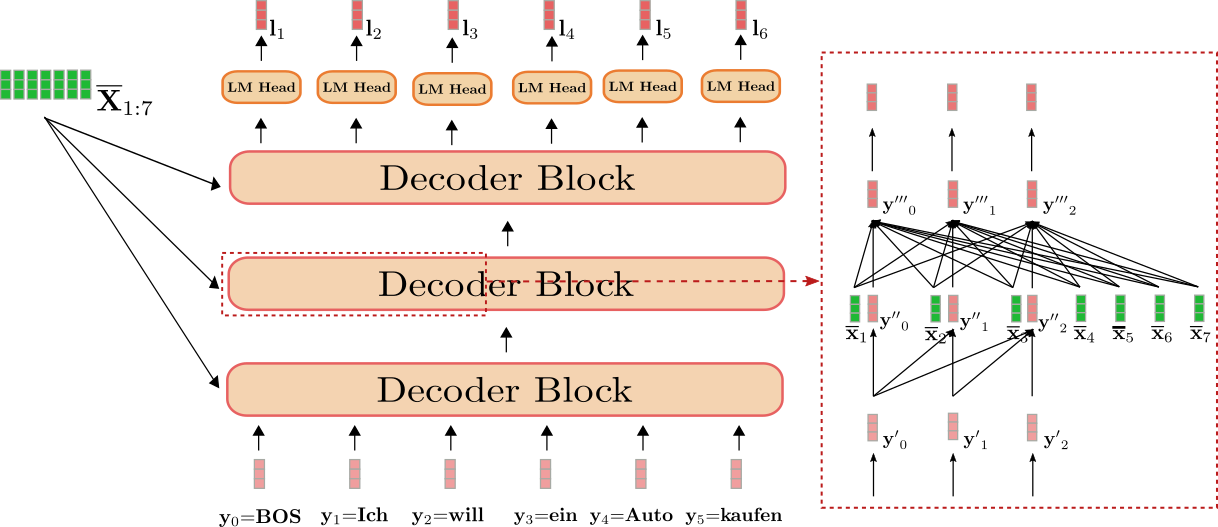
我们可以看到解码器将 \(\mathbf{Y}_{0:5}\): “BOS”、“Ich”、“will”、“ein”、“Auto”、“kaufen” (图中以浅红色显示) 和 “I”、“want”、“to”、“buy”、“a”、“car”、“EOS” ( 即 \(\mathbf{\overline{X}}_{1:7}\) (图中以深绿色显示)) 映射到 logit 向量 \(\mathbf{L}_{1:6}\) (图中以深红色显示)。
因此,对每个 \(\mathbf{l}_1、\mathbf{l}_2、\ldots、\mathbf{l}_6\) 使用 softmax 操作可以定义下列条件概率分布:
\[p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7}), \]\[\ldots, \]\[p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}) \]
总条件概率如下:
其可表示为以下乘积形式:
图右侧的红框显示了前三个目标向量 \(\mathbf{y}_0\)、\(\mathbf{y}_1\)、 \(\mathbf{y}_2\) 在一个解码器模块中的行为。下半部分说明了单向自注意机制,中间说明了交叉注意机制。我们首先关注单向自注意力。
与双向自注意一样,在单向自注意中, query 向量 \(\mathbf{q}_0, \ldots, \mathbf{q}_{m-1}\) (如下图紫色所示), key 向量 \(\mathbf{k}_0, \ldots, \mathbf{k}_{m-1}\) (如下图橙色所示),和 value 向量 \(\mathbf{v }_0, \ldots, \mathbf{v}_{m-1}\) (如下图蓝色所示) 均由输入向量 \(\mathbf{y'}_0, \ldots, \mathbf{ y'}_{m-1}\) (如下图浅红色所示) 映射而来。然而,在单向自注意力中,每个 query 向量 \(\mathbf{q}_i\) 仅 与当前及之前的 key 向量进行比较 (即 \(\mathbf{k}_0 , \ldots, \mathbf{k}_i\)) 并生成各自的 注意力权重 。这可以防止输出向量 \(\mathbf{y''}_j\) (如下图深红色所示) 包含未来向量 (\(\mathbf{y}_i\),其中 \(i > j\) 且 \(j \in {0, \ldots, m - 1 }\)) 的任何信息 。与双向自注意力的情况一样,得到的注意力权重会乘以它们各自的 value 向量并加权求和。
我们将单向自注意力总结如下:
请注意, key 和 value 向量的索引范围都是 \(0:i\) 而不是 \(0: m-1\),\(0: m-1\) 是双向自注意力中 key 向量的索引范围。
下图显示了上例中输入向量 \(\mathbf{y'}_1\) 的单向自注意力。
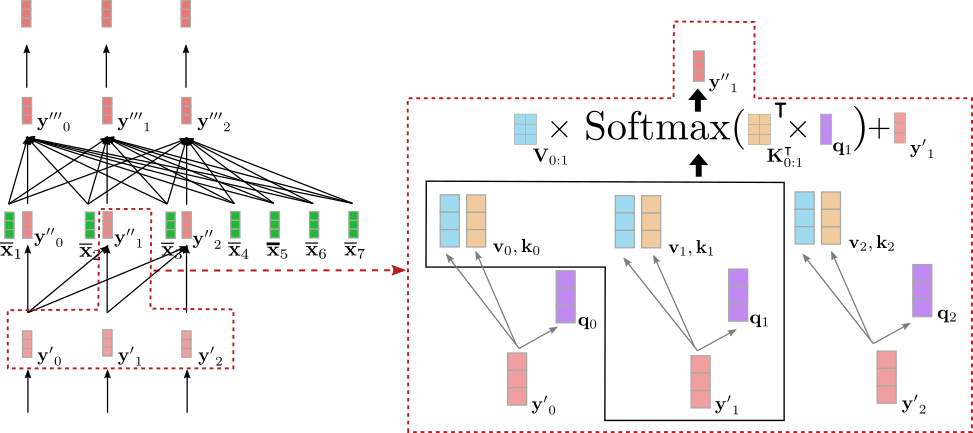
可以看出 \(\mathbf{y''}_1\) 只依赖于 \(\mathbf{y'}_0\) 和 \(\mathbf{y'}_1\)。因此,单词 “Ich” 的向量表征 ( 即 \(\mathbf{y'}_1\)) 仅与其自身及 “BOS” 目标向量 ( 即 \(\mathbf{y'}_0\)) 相关联,而 不 与 “will” 的向量表征 ( 即 \(\mathbf{y'}_2\)) 相关联。
那么,为什么解码器使用单向自注意力而不是双向自注意力这件事很重要呢?如前所述,基于 transformer 的解码器定义了从输入向量序列 \(\mathbf{Y}_{0: m-1}\) 到其 下一个 解码器输入的 logit 向量的映射,即 \(\mathbf{L}_{1:m}\)。举个例子,输入向量 \(\mathbf{y}_1\) = “Ich” 会映射到 logit 向量 \(\mathbf{l}_2\),并用于预测下一个输入向量 \(\mathbf{y}_2\)。因此,如果 \(\mathbf{y'}_1\) 可以获取后续输入向量 \(\mathbf{Y'}_{2:5}\)的信息,解码器将会简单地复制向量 “will” 的向量表征 ( 即 \(\mathbf{y'}_2\)) 作为其输出 \(\mathbf{y''}_1\),并就这样一直传播到最后一层,所以最终的输出向量 \(\mathbf{\overline{y}}_1\) 基本上就只对应于 \(\mathbf{y}_2\) 的向量表征,并没有起到预测的作用。
这显然是不对的,因为这样的话,基于 transformer 的解码器永远不会学到在给定所有前驱词的情况下预测下一个词,而只是对所有 \(i \in {1, \ldots, m }\),通过网络将目标向量 \(\mathbf{y}_i\) 复制到 \(\mathbf {\overline{y}}_{i-1}\)。以下一个目标变量本身为条件去定义下一个目标向量,即从 \(p(\mathbf{y} | \mathbf{Y}_{0:i}, \mathbf{\overline{ X}})\) 中预测 \(\mathbf{y}_i\), 显然是不对的。因此,单向自注意力架构允许我们定义一个 因果的 概率分布,这对有效建模下一个目标向量的条件分布而言是必要的。
太棒了!现在我们可以转到连接编码器和解码器的层 - 交叉注意力 机制!
交叉注意层将两个向量序列作为输入: 单向自注意层的输出 \(\mathbf{Y''}_{0: m-1}\) 和编码器的输出 \(\mathbf{\overline{X}}_{1:n}\)。与自注意力层一样, query 向量 \(\mathbf{q}_0, \ldots, \mathbf{q}_{m-1}\) 是上一层输出向量 \(\mathbf{Y''}_{0: m-1}\) 的投影。而 key 和 value 向量 \(\mathbf{k}_0, \ldots, \mathbf{k}_{n-1}\)、\(\mathbf{v}_0, \ldots, \mathbf {v}_{n-1}\) 是编码器输出向量 \(\mathbf{\overline{X}}_{1:n}\) 的投影。定义完 key 、value 和 query 向量后,将 query 向量 \(\mathbf{q}_i\) 与 所有 key 向量进行比较,并用各自的得分对相应的 value 向量进行加权求和。这个过程与 双向 自注意力对所有 \(i \in {0, \ldots, m-1}\) 求 \(\mathbf{y'''}_i\) 是一样的。交叉注意力可以概括如下:
注意,key 和 value 向量的索引范围是 \(1:n\),对应于编码器输入向量的数目。
我们用上例中输入向量 \(\mathbf{y''}_1\) 来图解一下交叉注意力机制。
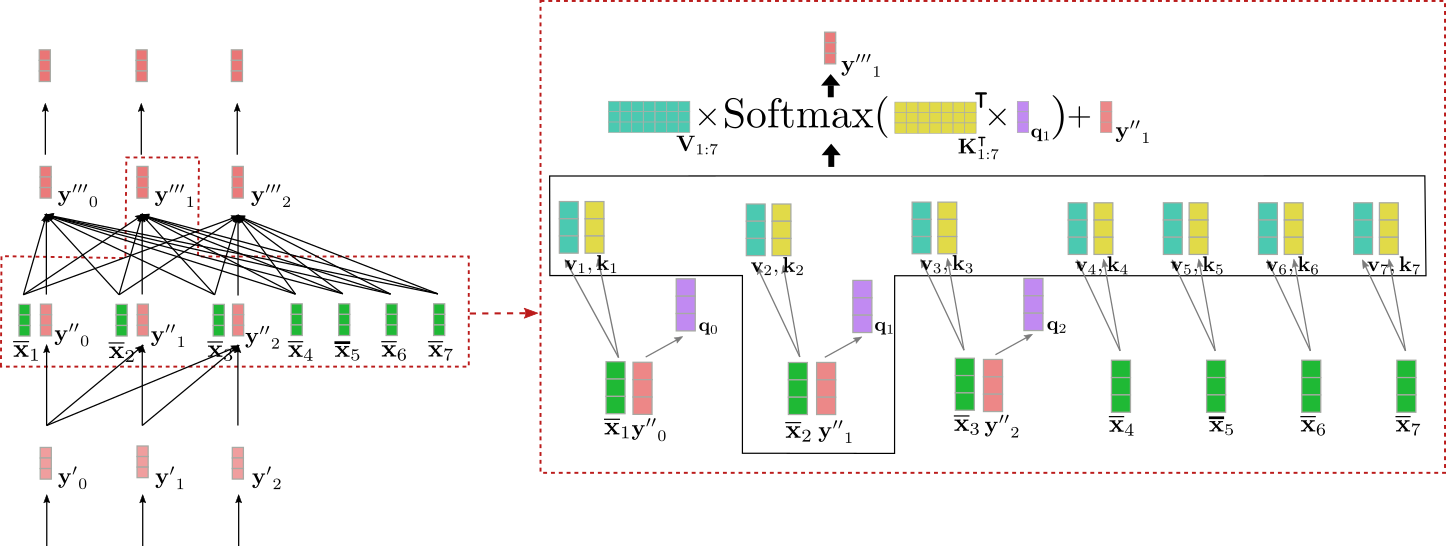
我们可以看到 query 向量 \(\mathbf{q}_1\)(紫色)源自 \(\mathbf{y''}_1\)(红色),因此其依赖于单词 "Ich" 的向量表征。然后将 query 向量 \(\mathbf{q}_1\) 与对应的 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_7\)(黄色)进行比较,这里的 key 向量对应于编码器对其输入 \(\mathbf{X}_{1:n}\) = "I want to buy a car EOS" 的上下文相关向量表征。这将 "Ich" 的向量表征与所有编码器输入向量直接关联起来。最后,将注意力权重乘以 value 向量 \(\mathbf{v}_1, \ldots, \mathbf{v}_7\)(青绿色)并加上输入向量 \(\mathbf{y''}_1\) 最终得到输出向量 \(\mathbf{y'''}_1\)(深红色)。
所以,直观而言,到底发生了什么?每个输出向量 \(\mathbf{y'''}_i\) 是由所有从编码器来的 value 向量(\(\mathbf{v}_{1}, \ldots, \mathbf{v}_7\) )的加权和与输入向量本身 \(\mathbf{y''}_i\) 相加而得(参见上图所示的公式)。其关键思想是: 来自解码器的 \(\mathbf{q}_i\) 的 query 投影与 来自编码器的 \(\mathbf{k}_j\) 越相关,其对应的 \(\mathbf{v}_j\) 对输出的影响越大。
酷!现在我们可以看到这种架构的每个输出向量 \(\mathbf{y'''}_i\) 取决于其来自编码器的输入向量 \(\mathbf{\overline{X}}_{1 :n}\) 及其自身的输入向量 \(\mathbf{y''}_i\)。这里有一个重要的点,在该架构中,虽然输出向量 \(\mathbf{y'''}_i\) 依赖来自编码器的输入向量 \(\mathbf{\overline{X}}_{1:n}\),但其完全独立于该向量的数量 \(n\)。所有生成 key 向量 \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) 和 value 向量 $\mathbf{v}_1, \ldots, \mathbf{v}_n $ 的投影矩阵 \(\mathbf{W}^{\text{cross}}_{k}\) 和 \(\mathbf{W}^{\text{cross}}_{v}\) 都是与 \(n\) 无关的,所有 \(n\) 共享同一个投影矩阵。且对每个 \(\mathbf{y'''}_i\),所有 value 向量 \(\mathbf{v}_1, \ldots, \mathbf{v}_n\) 被加权求和至一个向量。至此,关于为什么基于 transformer 的解码器没有远程依赖问题而基于 RNN 的解码器有这一问题的答案已经很显然了。因为每个解码器 logit 向量 直接 依赖于每个编码后的输出向量,因此比较第一个编码输出向量和最后一个解码器 logit 向量只需一次操作,而不像 RNN 需要很多次。
总而言之,单向自注意力层负责基于当前及之前的所有解码器输入向量建模每个输出向量,而交叉注意力层则负责进一步基于编码器的所有输入向量建模每个输出向量。
为了验证我们对该理论的理解,我们继续上面编码器部分的代码,完成解码器部分。
\({}^1\) 词嵌入矩阵 \(\mathbf{W}_{\text{emb}}\) 为每个输入词提供唯一的 上下文无关 向量表示。这个矩阵通常也被用作 “LM 头”,此时 “LM 头”可以很好地完成“编码向量到 logit” 的映射。
\({}^2\) 与编码器部分一样,本文不会详细解释前馈层在基于 transformer 的模型中的作用。Yun 等 (2017) 的工作认为前馈层对于将每个上下文相关向量 \(\mathbf{x'}_i\) 映射到所需的输出空间至关重要,仅靠自注意力层无法完成。这里应该注意,每个输出词元 \(\mathbf{x'}\) 对应的前馈层是相同的。有关更多详细信息,建议读者阅读论文。
from transformers import MarianMTModel, MarianTokenizer
import torch
tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()
# create token ids for encoder input
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids
# pass input token ids to encoder
encoder_output_vectors = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state
# create token ids for decoder input
decoder_input_ids = tokenizer("<pad> Ich will ein", return_tensors="pt", add_special_tokens=False).input_ids
# pass decoder input ids and encoded input vectors to decoder
decoder_output_vectors = model.base_model.decoder(decoder_input_ids, encoder_hidden_states=encoder_output_vectors).last_hidden_state
# derive embeddings by multiplying decoder outputs with embedding weights
lm_logits = torch.nn.functional.linear(decoder_output_vectors, embeddings.weight, bias=model.final_logits_bias)
# change the decoder input slightly
decoder_input_ids_perturbed = tokenizer("<pad> Ich will das", return_tensors="pt", add_special_tokens=False).input_ids
decoder_output_vectors_perturbed = model.base_model.decoder(decoder_input_ids_perturbed, encoder_hidden_states=encoder_output_vectors).last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear(decoder_output_vectors_perturbed, embeddings.weight, bias=model.final_logits_bias)
# compare shape and encoding of first vector
print(f"Shape of decoder input vectors {embeddings(decoder_input_ids).shape}. Shape of decoder logits {lm_logits.shape}")
# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `Ich` equal to its perturbed version?: ", torch.allclose(lm_logits[0, 0], lm_logits_perturbed[0, 0], atol=1e-3))
输出:
Shape of decoder input vectors torch.Size([1, 5, 512]). Shape of decoder logits torch.Size([1, 5, 58101])
Is encoding for `Ich` equal to its perturbed version?: True
我们首先比较解码器词嵌入层的输出维度 embeddings(decoder_input_ids) (对应于 \(\mathbf{Y}_{0: 4}\),这里 <pad> 对应于 BOS 且 "Ich will das" 被分为 4 个词) 和 lm_logits (对应于 \(\mathbf{L}_{1:5}\)) 的维度。此外,我们还通过解码器将单词序列 “<pad> Ich will ein” 和其轻微改编版 “<pad> Ich will das” 与 encoder_output_vectors 一起传递给解码器,以检查对应于 “Ich” 的第二个 lm_logit 在仅改变输入序列中的最后一个单词 (“ein” -> “das”) 时是否会有所不同。
正如预期的那样,解码器输入词嵌入和 lm_logits 的输出, 即 \(\mathbf{Y}_{0: 4}\) 和 \(\mathbf{L}_{ 1:5}\) 的最后一个维度不同。虽然序列长度相同 (=5),但解码器输入词嵌入的维度对应于 model.config.hidden_size,而 lm_logit 的维数对应于词汇表大小 model.config.vocab_size。其次,可以注意到,当将最后一个单词从 “ein” 变为 “das”,\(\mathbf{l}_1 = \text{“Ich”}\) 的输出向量的值不变。鉴于我们已经理解了单向自注意力,这就不足为奇了。
最后一点, 自回归 模型,如 GPT2,与删除了交叉注意力层的 基于 transformer 的解码器模型架构是相同的,因为纯自回归模型不依赖任何编码器的输出。因此,自回归模型本质上与 自编码 模型相同,只是用单向注意力代替了双向注意力。这些模型还可以在大量开放域文本数据上进行预训练,以在自然语言生成 (NLG) 任务中表现出令人印象深刻的性能。在 Radford 等 (2019) 的工作中,作者表明预训练的 GPT2 模型无需太多微调即可在多种 NLG 任务上取得达到 SOTA 或接近 SOTA 的结果。你可以在 此处 获取所有 🤗 transformers 支持的 自回归 模型的信息。
好了!至此,你应该已经很好地理解了 基于 transforemr 的编码器-解码器模型以及如何在 🤗 transformers 库中使用它们。
非常感谢 Victor Sanh、Sasha Rush、Sam Shleifer、Oliver Åstrand、Ted Moskovitz 和 Kristian Kyvik 提供的宝贵反馈。
附录
如上所述,以下代码片段展示了如何为 基于 transformer 的编码器-解码器模型编写一个简单的生成方法。在这里,我们使用 torch.argmax 实现了一个简单的 贪心 解码法来对目标向量进行采样。
from transformers import MarianMTModel, MarianTokenizer
import torch
tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids
# create BOS token
decoder_input_ids = tokenizer("<pad>", add_special_tokens=False, return_tensors="pt").input_ids
assert decoder_input_ids[0, 0].item() == model.config.decoder_start_token_id, "`decoder_input_ids` should correspond to `model.config.decoder_start_token_id`"
# STEP 1
# pass input_ids to encoder and to decoder and pass BOS token to decoder to retrieve first logit
outputs = model(input_ids, decoder_input_ids=decoder_input_ids, return_dict=True)
# get encoded sequence
encoded_sequence = (outputs.encoder_last_hidden_state,)
# get logits
lm_logits = outputs.logits
# sample last token with highest prob
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
# concat
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)
# STEP 2
# reuse encoded_inputs and pass BOS + "Ich" to decoder to second logit
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
# sample last token with highest prob again
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
# concat again
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)
# STEP 3
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)
# let's see what we have generated so far!
print(f"Generated so far: {tokenizer.decode(decoder_input_ids[0], skip_special_tokens=True)}")
# This can be written in a loop as well.
输出:
Generated so far: Ich will ein
在这个示例代码中,我们准确地展示了正文中描述的内容。我们在输入 “I want to buy a car” 前面加上 \(\text{BOS}\) ,然后一起传给编码器-解码器模型,并对第一个 logit $\mathbf{l}_1 $ (对应代码中第一次出现 lm_logits 的部分) 进行采样。这里,我们的采样策略很简单: 贪心地选择概率最高的词作为下一个解码器输入向量。然后,我们以自回归方式将采样得的解码器输入向量与先前的输入一起传递给编码器-解码器模型并再次采样。重复 3 次后,该模型生成了 “Ich will ein”。结果没问题,开了个好头。
在实践中,我们会使用更复杂的解码方法来采样 lm_logits。你可以参考 这篇博文 了解更多的解码方法。
至此,《基于 Transformers 的编码器-解码器模型》的四个部分就全部分享完啦,欢迎大家阅读其他分享 🤗!
英文原文: https://hf.co/blog/encoder-decoder
原文作者: Patrick von Platen
译者: Matrix Yao (姚伟峰),英特尔深度学习工程师,工作方向为 transformer-family 模型在各模态数据上的应用及大规模模型的训练推理。
审校/排版: zhongdongy (阿东)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号