机器学习之决策树

目录

• 1、决策树
• 2、决策树的构建
  • 2.1 特征选择
  • 2.2 特征树的生成
  • 2.3 特征树的剪枝
• 3、CART算法（classification and regression tree tree）

1、决策树

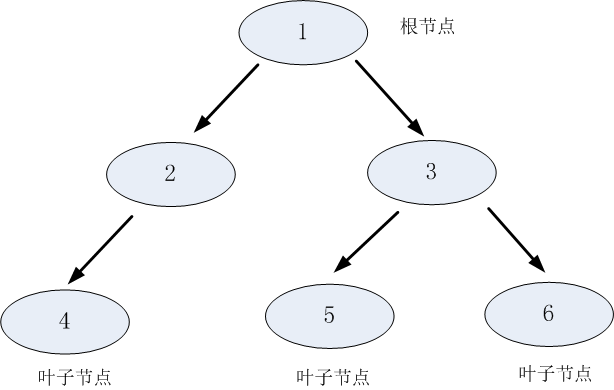
• 树：是由节点和边两种元素组成的结构。其中节点包括根结点、父节点、子节点和叶子节点。

• 决策树：利用树结构进行决策，每一个非叶子节点是一个特征，表示一个判断条件，每一个叶子节点是是一个类，表示结论。

• 分类决策树模型：是一种描述对实例进行分类的树形结构。

• 决策树过程：可以把决策树看成是一个if-then的集合，该集合由决策树的根结点(root node)到叶结点(leaf node)的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点的类对应着规则的结论。

• 互斥完备性：是决策树路径的重要性质。即每一个实例都被一条路径或一条规则所覆盖，而且只被一条路径或一条规则所覆盖。

• 决策树作预测的过程如下：

  1. 收集数据：例如，问卷调查、抽样调查、网站下载、爬虫爬取。
  2. 准备数据：将数据进行整理，形成csv、excel等格式的数据文件。
  3. 分析数据：针对要使用的决策树算法，检查该结构化数据是否符合预期，即是否是需要的数据；另外可能需要对数据进行填充，可视化，数据编码，数据降维，数据融合等操作。
  4. 训练算法模型：该过程即利用预处理后的数据构建一个决策树的数据结构。
  5. 测试模型：使用经验树计算错误率，检查是否满足要求，不满足时需要改善。
  6. 使用模型：基本上适用于任何监督学习算法。

2、决策树的构建

• 决策树的构建过程包括三个步骤：特征选择、决策树的生成和决策树的剪枝。

2.1 特征选择

• 特征选择：主要是选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率，否则容易成为随机分类。特征选择就是决定用哪个特征来划分特征空间。
• 特征选择标准：信息增益、信息增益比和基尼系数。
  1. ID3算法（以信息增益为标准）
  2. C4.5算法（以信息增益比为标准）
  3. CART分类树算法（以基尼系数为标准）
• 特征选择的原理：首先得到数据集，然后基于最好的属性值划分数据集，由于数据可能有多个特征，因此需要对多个特征分支进行数据集的划分。第一次划分后，数据集被向下传递到树的分支的下一个节点。然后下一个节点再基于下一个特征进行特征选择，再次划分数据集。可采用递归原则处理数据集。

（1）信息增益

• 信息增益：待分类的数据集合的熵和选定某个特征的条件熵之差。信息增益是样本集合纯度最常用的一种指标，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大，即该属性特征对最终的分类结果影响也就越大。计算公式为：
  \[g(D,A) = H(D) - H(D|A) \]

其中，\(g(D,A)\)是熵\(H(D)\)与条件熵\(H(D|A)\)之差，称为互信息，\(D = \{X_{1}, X_{2},...,X_{n}\}\)。决策树中的信息增益等价于训练数据集中类与特征的互信息。

• 熵：表示随机变量不确定性的度量。也称经验熵，熵越大，随机变量的不确定性就越大。假设X是一个取值有限的离散随机变量\(X={x_{1},x_{2},...,x_{n}}\)。对于数据集，\(X\)可以理解为特征属性，而\({x_{1},x_{2},...,x_{n}}\)表示该特征下的每个类别标签。其概率分布为：\(P(X=x_{i}) = p_{i}, i =1,2,...,n\)，则随机变量X的熵定义为：
  \[H(X) = - \sum_{i=1}^{n} p_{i} logp_{i} \]

也可以写成$$H(p) = - \sum_{i=1}^{n} p_{i} log_{2} p_{i}$$
其中，\(p_{i} = \frac{|c_{k}|}{|D|}\)，因此经验条件熵也可以写成：
$$H(D) = - \sum_{i=1}^{K} \frac{|c_{k}|}{|D|} log_{2} \frac{|c_{k|}}{|D|}$$
其中D是数据集，|D|表示样本容量，即样本个数。\(c_{k}\)表示第k个类别标签，而\(|c_{k}|\)表示第k个类别的样本个数，第c个特征有K个类。

• 条件熵：表示在已知随机变量X的条件下随机变量Y的不确定性。也称经验条件熵，假设有随机变量\((X,Y)\)，其联合概率分布为：\(P(X=x_{i}, Y=y_{i}) = p_{ij}, i=1,2,..,n;j=1,2,...,m\)，计算公式为：
  \[H(Y|X) = \sum_{i=1}^{n} p_{i}H(Y|X=x_{i}) \]

以信息增益为标准的特征选择代码在胡歌的github

• 信息增益的缺点：信息增益偏向取值较多的特征。原因是当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较 偏向取值较多的特征。

（2）信息增益比

• 信息增益比：实质是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。信息增益比越大，则该属性特征对最终的分类结果影响也就越大。计算公式为：
  \[g_{R}(D, A) = \frac{g(D,A)}{H_{A}(D)} \]

其中，\(H_{A}(D) = -\sum_{i=1}^{n} \frac{|D_{i}|}{|D|} log_{2} \frac{|D_{i}|}{|D|}\)，\(n\)表示特征A的取值个数。
-惩罚参数：数据集D以特征A作为随机变量的熵的倒数，即：将特征A取值相同的样本划分到同一个子集中之前所说数据集的熵是依据类别进行划分的）
$$惩罚参数 = \frac{1}{H_{A}^{D}} = \frac{1}{- \sum_{i=1}^{n} \frac{|D_{i}|}{|D|} log_{2} \frac{|D_{i}|}{|D|} }$$

以信息增益比为标准的特征选择代码在胡歌的github

• 信息增益比的缺点：信息增益比偏向取值较少的特征。当特征取值较少时HA(D)的值较小，因此其倒数较大，因而信息增益比较大。因而偏向取值较少的特征。

（3）基尼指数

• 基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。定义为：
  \[基尼指数 = 样本被选中的概率 * 样本被分错的概率 \]

计算公司如下：
$$Gini(p) = \sum_{k=1}^{K} p_{k} (1-p_{k}) = 1 - \sum_{k=1}^{K} p_{k}^{2}$$
其中，pk表示选中的样本属于k类别的概率，则这个样本被分错的概率是(1-pk)；样本集合中有K个类别，一个随机选中的样本可以属于这k个类别中的任意一个，因而对类别就加和；当为二分类是，Gini(P) = 2p(1-p)。

• 样本集合D的基尼指数为：

  \[Gini(p) = 1 - \sum_{k=1}^{K} p_{k}^{2} = 1 - \sum_{k=1}^{K} (\frac{|c_{k}|}{|D|})^{2} \]

• 基于特征A划分样本集合D之后的基尼指数：指某个特征值将样本集合D划分为两个子集的纯度：

  \[Gini(D,A) = \frac{|D_{1}|}{|D|} Gini(D_{1}) + \frac{|D_{2}|}{|D|} Gini(D_{2}) \]

2.2 特征树的生成

• 决策树的生成算法有多种，包括ID3算法，C4.5算法。
• ID3算法：核心是指在决策树各个节点上以信息增益为标准进行特征选择，递归地构建决策树。
• C4.5算法：核心是以信息增益比为标准进行特征选择，递归构建决策树。

输入：训练数据集D，特征集A，阈值threshold
输出：决策树T.
1.检查D中所有数据标签是否为同一类，是同一类，T直接为单节点树，并将此类标记为该结点的类标记并返回T。
2.若,则T为单结点树，并将D中实例数最大的类作为该结点的标记，返回T。
3.否则，按照特征选择方法中的信息增益(信息增益比)方法计算A中各特征的信息增益(信息增益比)，选择信息增益(比)最大的特征，并检测其增益(比)是否大于阈值。
4.对大于阈值的信息增益(比)特征，对其每一个可能的值将数据集D进行分割为若干非空子集并构建子结点。
5.重复分割步骤，分割特征不包括之前已经分割过的特征，当分割后的信息增益(比)不大于阈值时，将此结点下的实例数最多的类作为此结点的标记，构成一个叶结点。

2.3 特征树的剪枝

• 决策树的剪枝：由于决策树对训练数据集进行训练，分类很准确，但是对未知的测试数据的分类却没有那么准确，即容易出现过拟合现象。因此需要对已经生成的树进行简化，这个过程成为剪枝。剪枝往往通过极小化决策树整体的损失函数或代价来实现。
• 过拟合：是指所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越，导致在验证数据集以及测试数据集中表现不佳。
• 欠拟合：欠拟合是指模型拟合程度不高，数据距离拟合曲线较远，或指模型没有很好地捕捉到数据特征，不能够很好地拟合数据。即不能很好地识别测试数据。
• 剪枝的算法原理为：

\[C_{\alpha}(T) = C(T)+ \alpha |T| \]

其中\(C(T) = \sum_{t=1}^{|T|} N_{t}H_{t}(T)\)表示模型对训练数据的预测误差，\(H_(t)(T) = -\sum_{k=1}^{K} \frac{N_{tk}}{N_{t}} log \frac{N_{tk}}{N_{t}}\)表示经验熵。
\(|T|\)是叶结点个数，表示模型的复杂度，\(N_{t}\)表示叶结点t的样本个数，\(N_{tk}\)表示第k类样本的个数。
\(\alpha\)表示剪枝参数，用于控制拟合程度和模型复杂度的平衡。较大的\(\alpha\)能促使选择简单的树，较小的\(\alpha\)能促使选择复杂的树。

3、CART算法（classification and regression tree tree）

• CART，即分类与回归树，是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假定决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。
• CART算法分为两个步骤：
  1. 决策树生成：基于训练集生成决策树，生成的决策树要尽量大；
  2. 决策树剪枝：基于验证数据对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准。

详细的CART请参考：https://www.cnblogs.com/hugechuanqi/p/10549640.html

参考

1. Jack Cui的机器学习基础：https://cuijiahua.com/blog/2017/11/ml_2_decision_tree_1.html：
2. 李航《统计学习方法》
3. 决策树之特征选择标准：https://www.cnblogs.com/muzixi/p/6566803.html