python实现的栈及算法应用（括号匹配、进制转换、前中后缀表达式）

栈的定义

class Stack:
    """
    items[0]为栈底
    """
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        return self.items[-1]
    def size(self):
        return len(self.items)

应用（一）括号匹配

只匹配小括号()

def parChecker(symbolString):
    """
    判断括号是否成对匹配
    :param symbolString:
    :return:
    """
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()
        index += 1
    if s.isEmpty() and balanced:
        print("匹配成功", s.size())
    else:
        print("匹配失败", s.size())

通用{}[]()

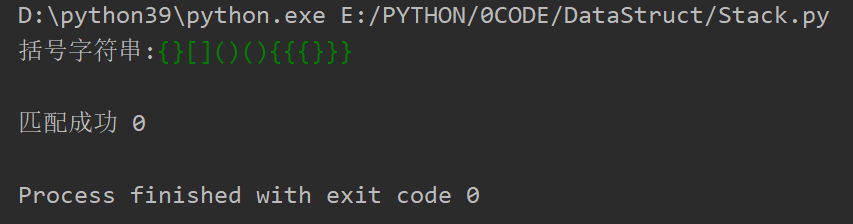
def matches(open, close):
    opens = "([{"
    closes = ")]}"
    return opens.index(open) == closes.index(close)

# def parChecker2(symbolString):
#     """
#     判断括号是否成对匹配
#     :param symbolString:
#     :return:
#     """
#     s = Stack()
#     balanced = True
#     index = 0
#     while index < len(symbolString) and balanced:
#         symbol = symbolString[index]
         if symbol in "([{":
#             s.push(symbol)
#         else:
#             if s.isEmpty():
#                 balanced = False
#             else:
                 top = s.pop()
                 if not matches(top, symbol):
                     balanced = False
# 
#         index += 1
#     if s.isEmpty() and balanced:
#         print("匹配成功", s.size())
#     else:
#         print("匹配失败", s.size())

应用（二）进制转换-除n取余法

十进制转二进制

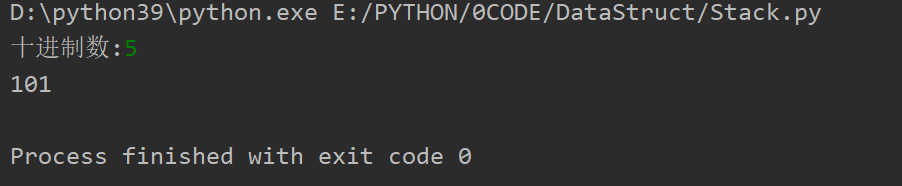
def divideBy2(d):
    """
    十进制 ==> 2进制
    :param d:
    :return:
    """
    s = Stack()
    while d > 0:
        b = d % 2
        s.push(b)
        d //= 2

    binstr = ""
    while s.size() > 0:
        binstr += str(s.pop())

    print(binstr)

十进制转十六以下任意进制

其实我们还可以扩展到n进制，多用一些字母代替数字即可。

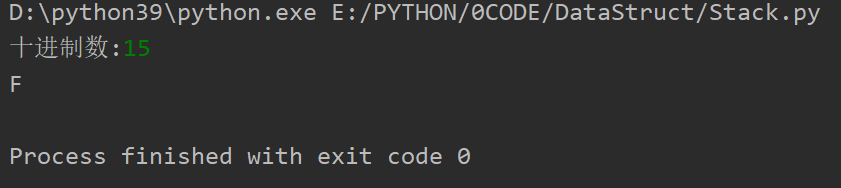
def baseConverter(d):
    """
    十进制 ==> 16以下任意进制
    :return:
    """
    base = 16
    digits = "0123456789ABCDEF"
    s = Stack()
    while d > 0:
        b = d % base
        s.push(b)
        d //= base

    basestr = ""
    while s.size() > 0:
        basestr += str(s.pop())

    print(basestr)

应用（三）算术表达式转换&求值

术语
中缀表达式(运算符在数字中间): A+BC
全括号中缀表达式: ((A+(BC))+D)
前缀表达式: +AB代表A+B
后缀表达式: AB+代表A+B

结论:距离操作数最近的操作符越优先参与运算

中缀表达式转后缀表达式

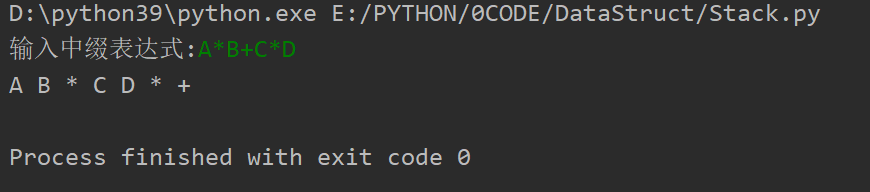
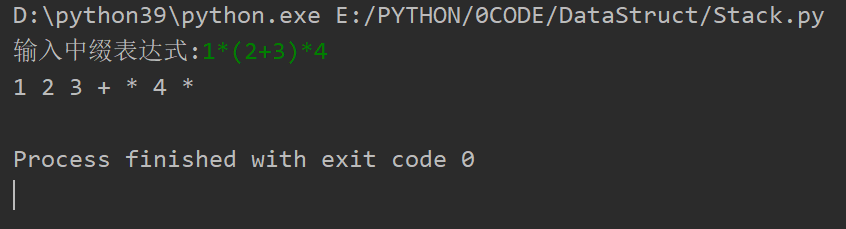
算法：
从左到右扫描中缀表达式
遇到操作数123...ABC...，直接输出
遇到左括号（，压入栈s
遇到右括号），一直弹出栈顶操作符（并输出）直到遇到左括号
遇到操作符+-*/，
（1）优先级大于栈顶操作符，压入栈s
（2）优先级小于栈顶操作符，一直弹出栈顶操作符（并输出）直到大于栈顶操作符后，压入栈s
扫描完毕，弹出栈s中所有操作符（并输出）

def infixTOpostfix(infixstr):
    """
    中缀表达式 ==> 后缀表达式
    :param infixstr:
    :return:
    """
    prec = {}
    prec['*'] = 3
    prec['/'] = 3
    prec['+'] = 2
    prec['-'] = 2
    prec['('] = 0

    s = Stack()
    pflist = []
    iflist = list(infixstr)

    for c in iflist:
        if c in "0123456789" or c in "ABCDEFJHIJKLMN":
            pflist.append(c)
        elif c == "(":
            s.push(c)
        elif c == ")":
            top = s.pop()
            while top != "(":
                pflist.append(top)
                top = s.pop()
        else:
            while (not s.isEmpty()) and prec[c] <= prec[s.peek()]:
                pflist.append(s.pop())
            s.push(c)

    while not s.isEmpty():
        pflist.append(s.pop())

    print(" ".join(pflist))

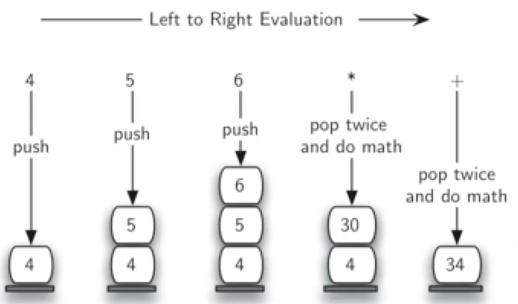
后缀表达式计算

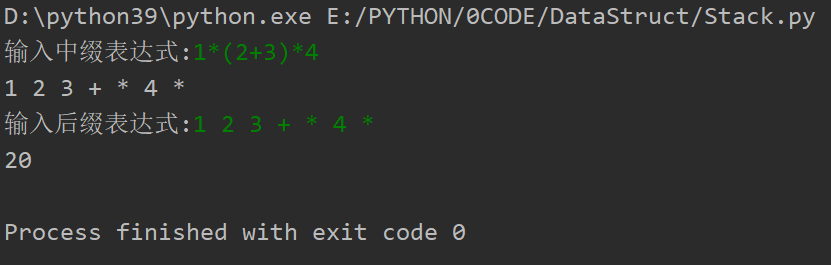
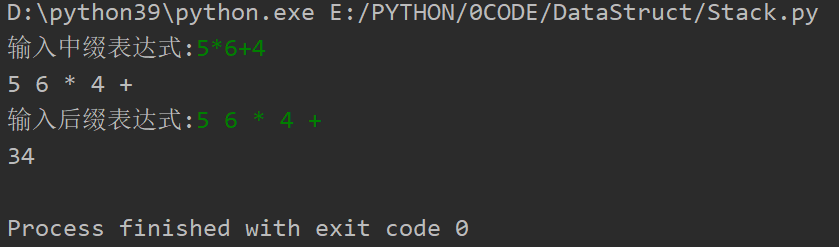
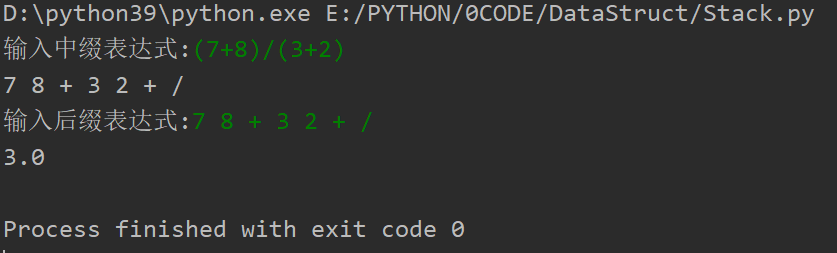
算法：
从左到右扫描后缀表达式
遇到数字，压入栈s
遇到操作符，弹出两个操作数op2, op1,把计算得到的结果压入栈s
直到扫描完毕，此时栈中仅剩一个元素，即为计算结果

def doMath(c, op1, op2):
    if c == "+":
        return op1 + op2
    elif c == "-":
        return op1 - op2
    elif c == "*":
        return op1 * op2
    elif c == "/":
        return op1 / op2

def postfixEval(postfixstr):
    s = Stack()
    pflist = postfixstr.split()

    for c in pflist:
        if c in "0123456789":
            s.push(int(c))
        else:
            op2 = s.pop()  # 先弹出的是右操作数(计算减法和除法时操作数左右顺序有区分)
            op1 = s.pop()
            res = doMath(c, op1, op2)
            s.push(res)

    print(s.pop())