算法分析-线性时间排序,决策树,计数排序,基数排序,桶排序【线性排序】
决策树引导
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑(声明:此决策树纯属为了写文章而YY的产物,没有任何根据,也不代表任何女孩的择偶倾向,请各位女同胞莫质问我^_^):
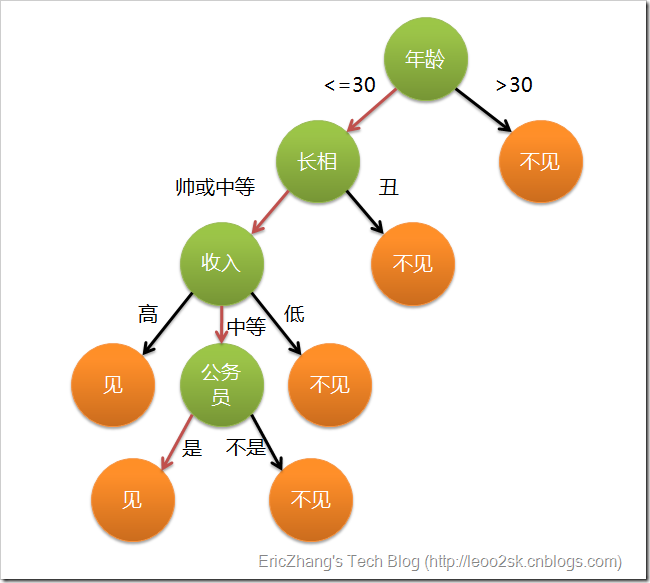
上图完整表达了这个女孩决定是否见一个约会对象的策略,其中绿色节点表示判断条件,橙色节点表示决策结果,箭头表示在一个判断条件在不同情况下的决策路径,图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,如果将所有条件量化,则就变成真正的决策树了。
有了上面直观的认识,我们可以正式定义决策树了:
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。知道了决策树的定义以及其应用方法,下面介绍决策树的构造算法。
下面给出A[1,2,3]排序的决策树,是算法导论的原图:
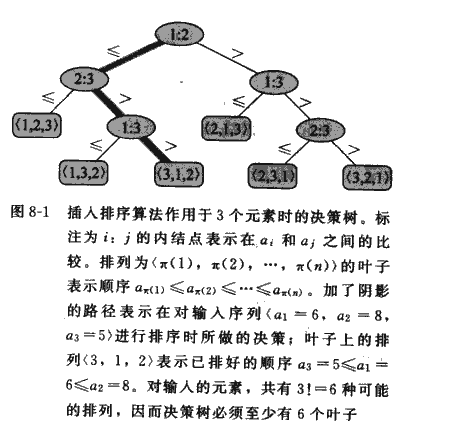

思考:
在一颗比较排序算法的决策树中,一个叶结点可能的最小深度是多少?
分析:
最少进行n-1次比较,所以深度最小是n-1



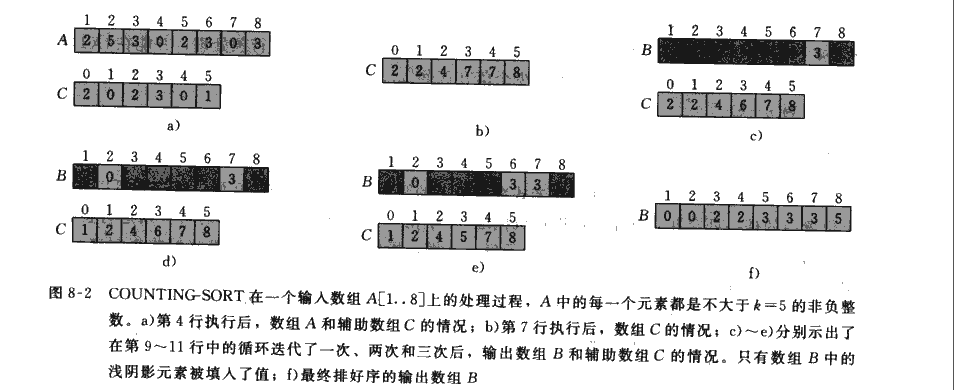


下面给出代码:
COUNTING-SORT 在数组 A={6,0,2,0,1,3,4,6,1,3,2}上的操作过程。
(1)C[1..k]被初始化为0。
(2)把等于A[j]的个数C[A[j]]进行循环累加 C[6]=1+1=2 C[0]=1+1=2 C[2]=1+1=2 C[1]=1+1=2 C[3]=1+1=2 C[4]=1
(3)把小于等于A[j]的个数C[A[j]]进行循环累加。
C[0]=2
C[1]=C[1]+C[0]=2+2=4
C[2]=C[2]+C[1]=2+4=6
C[3]=C[3]+C[2]=2+6=8
C[4]=C[4]+C[3]=1+8=9
C[5]=C[5]+C[4]=0+9=9
C[6]=C[6]+C[5]=2+9=11
(4)把A[j]放入到恰当的B[C[A[j]]]位置中去。
B[C[2]]=B[6]=2 C[2]-- C[2]=5
B[C[3]]=B[8]=3 C[3]-- C[3]=7
B[C[1]]=B[4]=1 C[1]-- C[1]=3
B[C[6]]=B[11]=6 C[6]-- C[6]=10
B[C[4]]=B[9]=4 C[4]-- C[4]=8
B[C[3]]=B[7]=3 C[3]-- C[3]=6
B[C[1]]=B[3]=1 C[1]-- C[1]=2
B[C[0]]=B[2]=0 C[0]-- C[0]=1
B[C[2]]=B[5]=2 C[2]-- C[2]=4
B[C[0]]=B[1]=0 C[0]-- C[0]=0
B[C[6]]=B[10]=6 C[6]-- C[6]=9 所以:B[10]={0,0,1,4,2,2,3,3,4,6,6}
1 Array.prototype.swap = function (i, j) { 2 var temp = this[j]; 3 this[j] = this[i]; 4 this[i] = temp; 5 }; 6 7 Array.prototype.getMaxVal = function () { 8 //可以用任意我们学过的排序方法写,我们学过冒泡,选择,归并,快排,堆排序。 9 //当然这样我们只要取出最大值即可,不需要全部排序,但是为了学程序,我将给出我们已经学过的所有排序方法,并全部排序 10 var r = this.length - 1; 11 // return this.BUBBLE_SORT()[r]; 12 // return this.SELECT_SORT()[r]; 13 // return this.QUICK_SORT(0, r)[r]; 14 //heap_size = r+1; return.this.HRAP_SORT()[r]; 15 // return this.MERGE_SORT(0,r)[r]; 16 return this.INSERT_SORT()[r]; 17 }; 18 //冒泡 19 Array.prototype.BUBBLE_SORT = function () { 20 21 //冒泡就是两两将换, 22 for (var i = this.length - 1; i > 0; i--) { 23 for (var j = 0; j < i; j++) { 24 if (this[j] > this[j + 1]) { 25 this.swap(j, j + 1); 26 } 27 } 28 } 29 return this; 30 }; 31 32 33 //选择排序 34 35 Array.prototype.SELECT_SORT = function () { 36 for (var i = 0; i < this.length - 1; i++) { 37 var min = this[i]; //默认选择第一个最小; 38 var index = i; //记录最小值的坐标 39 40 for (var j = i + 1; j < this.length; j++) { 41 if (this[j] < min) { 42 min = this[j]; 43 index = j; 44 } 45 } 46 this.swap(index, i); 47 } 48 return this; 49 }; 50 51 52 //随机算法-快排 53 //思想就是分治,递归。 54 //最主要的函数就是PARTITION,返回下标i,i的左边都比A[i]小,右边比他大; 55 Array.prototype.PARTITION = function (p, r) { 56 var i = p - 1; 57 var x = this[r]; 58 for (var j = p; j <= r - 1; j++) { 59 if (this[j] < x) { 60 this.swap(++i, j); 61 62 } 63 64 } 65 this.swap(++i, r); 66 return i; 67 }; 68 69 Array.prototype.RANDOM_PARTION = function (p, r) { 70 71 var q = p + Math.round(Math.random() * (r - p)); 72 this.swap(q, r); 73 return this.PARTITION(p, r); 74 }; 75 76 Array.prototype.QUICK_SORT = function (p, r) { 77 if (r > p) { 78 var q = this.RANDOM_PARTION(p, r); 79 arguments.callee.call(this, p, q - 1); 80 arguments.callee.call(this, q + 1, r); 81 } 82 return this; 83 }; 84 85 86 //堆排序 87 //其核心函数在于MAX_HRAPTITY,总能让i位置是最大的。 88 var heap_size = 0; //包含heap_size下标在内的,之后的下标都是排序好的。 89 90 Array.prototype.HEAP_SORT = function () { 91 this.BUILD_MAX_HEAP(); 92 while (heap_size > 1) { 93 this.swap(0, --heap_size); 94 this.MAX_HEAPTIFY(0); 95 } 96 heap_size = this.length; //最后复原 97 return this; 98 }; 99 100 //生成最大堆 101 Array.prototype.BUILD_MAX_HEAP = function () { 102 103 for (var i = Math.floor(this.length / 2) - 1; i >= 0; i--) { 104 this.MAX_HEAPTIFY(i); 105 } 106 }; 107 108 //生成以i为根节点,它为最大值 109 Array.prototype.MAX_HEAPTIFY = function (i) { 110 var largest = i; 111 var l = i * 2 + 1; 112 var r = i * 2 + 2; 113 114 if (l < heap_size && this[l] > this[largest]) { 115 116 largest = l; 117 } 118 119 if (r < heap_size && this[r] > this[largest]) { 120 121 largest = r; 122 } 123 if (largest !== i) { 124 this.swap(largest, i); 125 arguments.callee.call(this, largest); 126 } 127 }; 128 129 //heap_size = A.length; 130 //归并排序 131 //其核心思想是分治,递归 132 133 Array.prototype.MERGE_SORT = function (start, end) { 134 135 if (end > start) { //记住这里没有等号,不然会一直递归下去。 136 var middle = Math.floor((start + end) / 2); 137 arguments.callee.call(this, start, middle); 138 arguments.callee.call(this, middle + 1, end); 139 this.MEAGE(start, middle, end); 140 } 141 return this; 142 }; 143 144 Array.prototype.MEAGE = function (s, m, e) { 145 var A = this.slice(s, m + 1), 146 B = this.slice(m + 1, e + 1), 147 lenA = m + 1 - s, 148 lenB = e - m, 149 i = 0, 150 j = 0; 151 152 while (i < lenA && j < lenB) { 153 A[i] < B[j] ? this[s++] = A[i++] : this[s++] = B[j++]; 154 } 155 while (i < lenA) { 156 this[s++] = A[i++]; 157 } 158 while (j < lenB) { 159 this[s++] = B[j++]; 160 } 161 }; 162 163 164 //插入排序 165 Array.prototype.INSERT_SORT = function () { 166 try { 167 if (this.length < 1) { 168 throw new Error("错误长度的数组"); 169 } 170 for (var i = 1; i < this.length; i++) { 171 var j = i - 1, 172 temp = this[i]; 173 while (this[j] > temp && j >= 0) { 174 this[j + 1] = this[j]; 175 j--; 176 } 177 this[j + 1] = temp; 178 } 179 180 } catch (e) { 181 console.error(e); 182 } finally { 183 return this; 184 } 185 }; 186 187 //初始化数组全为0; 188 Array.prototype.setZero4arr = function (k) { 189 var B = []; 190 for (var i = 0; i <= k; i++) { 191 B[i] = 0; 192 } 193 return B; 194 }; 195 196 197 var A = [6, 0, 2, 0, 1, 3, 4, 6, 1, 3, 2], 198 k = A.getMaxVal(), 199 B = A.setZero4arr(A.length - 1); //最后放入 200 201 //计数排序 202 Array.prototype.COUNT_SORT = function (max, B) { 203 204 var C = this.setZero4arr(max); //0...max 205 206 207 for (var i = 0; i < this.length; i++) { 208 C[this[i]]++; //知道了每个数的个数 209 } 210 211 //累加得到最后的结果 C[i]包含了<= i 的个数。 212 for (var j = 1; j < C.length; j++) { 213 C[j] += C[j - 1]; 214 } 215 //最后填充B 216 for (var k = this.length - 1; k >= 0; k--) { 217 B[C[this[k]] - 1] = this[k]; 218 219 //由于每个元素可能都不相同,因此,每当将一个值A[k]放入数组B中的时候,都要减少C[A[k]]的值, 220 //这会使得下一个其值等于A[k]的输入元素(如果存在的话)直接进入输出数组B中A[k]的前一个位置。 221 C[this[k]]--; 222 223 } 224 return B; 225 }; 226 227 //思考 这样写对吗?稳定吗?看下面的思考题。 228 /*Array.prototype.COUNTING_SORT = function (k, B) { 229 230 var C = this.setZero4arr(k); 231 232 for (var i = 0; i < this.length; i++) { 233 C[this[i]]++; 234 } 235 for (var j = 1; j < C.length; j++) { 236 C[j] += C[j - 1]; 237 } 238 239 for (var k = 0; k < this.length; k++) { 240 B[C[this[k]] - 1] = this[k]; 241 C[this[k]]--; 242 } 243 return B; 244 245 };*/ 246 247 248 console.log(A.COUNTING_SORT(k, B));
8.2-2 试证明COUNTING-SORT是稳定的。
由8.2-1例子可以发现 开始时候B[6]=2,这个是数组靠后位置的2,因为第4个循环是从后往前循环的,所以经过多次j--后,到了B[5]=2 这是考前位置的2.所以由8.2-1例子可以看出,原数组A靠后相同的数放到了新数组B靠后的位置,而原数组A靠前的数放到了新数组B靠前的位置。所以COUNTING-SORT是稳定的。
8.2-3 假设我们在COUNTING-SORT的第10行循环开始部分,将代码改写为:10.for j=1 to A.length 试证明该算法仍然正确,它还稳定吗?
如果把第10行改成for j=1 to A.length ,颠倒顺序处理元素的顺序,那么还是8.2-1的例子,其中的第(4)个循环就要微调了,对于相同元素来说,原数组靠前的相同元素出现在新数组靠后的位置上,反之亦然。所以就不稳定了。
8.2-4 设计一个算法,它能够对于任何给定的驾驭0到K之间的n个整数先进行预处理,然后再O(1)时间内回答输入的n个整数中有多少个落在区间[a..b]内你设计的算法预处理时间应为Θ(n+k).
在n个整数中,通过第(3)个循环,计算出小于a值得元素个数C[a-1],小于等于b值得元素个数C[b],两者差值就是在[a,b]区间上的元素个数。
设落在区间[a,b]上元素个数x=C[b]-C[a-1].
基数排序
基数排序不需要比较关键字的大小。
它是根据关键字中各位的值,通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。
不妨通过一个具体的实例来展示一下,基数排序是如何进行的。
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我们知道,任何一个阿拉伯数,它的各个位数上的基数都是以0~9来表示的。
所以我们不妨把0~9视为10个桶。
我们先根据序列的个位数的数字来进行分类,将其分到指定的桶中。例如:R[0] = 50,个位数上是0,将这个数存入编号为0的桶中。
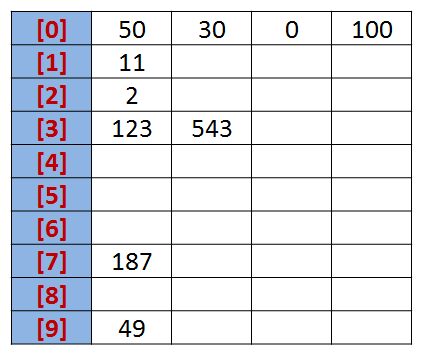
分类后,我们在从各个桶中,将这些数按照从编号0到编号9的顺序依次将所有数取出来。
这时,得到的序列就是个位数上呈递增趋势的序列。
按照个位数排序: {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
接下来,可以对十位数、百位数也按照这种方法进行排序,最后就能得到排序完成的序列。


8.3-2 下面的排序算法中哪些是稳定的,插入排序,归并排序,堆排序和快速排序?给出一个能使任何排序算法都稳定的方法。
归并和插入排序是稳定的,因为他们不改变相同元素原有的顺序。堆排序和快速排序是不稳定的。如果想让以上4种排序都是稳定排序,那么我们保存原数组相同元素的下标,在进行比较排序时,不同元素肯定没有这个问题,而相同元素在原数组中较小的下标对应的值放入到前面,较大的放到后面。
下面我给出基数排序的一个算法实现代码:
1 //基数排序 2 //他是基于计数排序的。 3 4 Array.prototype.COUNTING_SORT_4_RDIEX_SORT = function (b, d) { 5 var C = this.setZero4arr(9); //计数排序第一步 6 var B = this.setZero4arr(this.length - 1); 7 8 for (var j = 0; j < this.length; j++) { //计数排序第二步 9 10 C[get_bit_val(this[j], b, d)]++; 11 } 12 13 for (var k = 1; k < C.length; k++) { //计数排序第三步 14 C[k] += C[k - 1]; 15 } 16 17 for (var i = this.length - 1; i >= 0; i--) { //计数排序第四步 18 B[C[get_bit_val(this[i], b, d)] - 1] = this[i]; 19 C[get_bit_val(this[i], b, d)]--; //这一步很关键,如果遇到重复的,以前是往前插入了,不然会覆盖。 20 } 21 return B; 22 }; 23 24 //获得该数字第i位的数字,从个位开始取,如果没有这位的数,默认为0。 25 /* 26 * x是传入的数 27 * i是第几位 28 * 最大数的长度 29 * 30 * */ 31 function get_bit_val(x, i, d) { 32 x += ""; 33 var temp = x.split(""); 34 while (temp.length < d) { 35 temp.unshift(0); //往前填充0 36 } 37 return temp[i]; 38 } 39 40 41 Array.prototype.RDIEX_SORT = function () { 42 var k = this.getMaxVal().toString(); 43 var d = k.length; 44 var B = []; 45 for (var i = d - 1; i >= 0; i--) { 46 i == d - 1 ? B = this.COUNTING_SORT_4_RDIEX_SORT(i, d) : B = this.COUNTING_SORT_4_RDIEX_SORT.call(B, i, d); 47 } 48 return B; 49 }; 50 51 var A = [16, 22, 2, 323320, 13, 3, 2321, 45546, 5766, 7, 23]; 52 console.log(A.RDIEX_SORT());
桶排序Bucket sort
补充说明三点
1,桶排序是稳定的
2,桶排序是常见排序里最快的一种,比快排还要快…大多数情况下
3,桶排序非常快,但是同时也非常耗空间,基本上是最耗空间的一种排序算法
二.算法描述
例如要对大小为[1..1000]范围内的n个整数A[1..n]排序,可以把桶设为大小为10的范围,具体而言,设集合B[1]存储[1..10]的整数,集合B[2]存储(10..20]的整数,……集合B[i]存储((i-1)*10, i*10]的整数,i = 1,2,..100。总共有100个桶。然后对A[1..n]从头到尾扫描一遍,把每个A[i]放入对应的桶B[j]中。 然后再对这100个桶中每个桶里的数字排序,这时可用冒泡,选择,乃至快排,一般来说任何排序法都可以。最后依次输出每个桶里面的数字,且每个桶中的数字从小到大输出,这样就得到所有数字排好序的一个序列了。
下图表示出了桶排序作用于有10个数的输入数组上的操作过程。



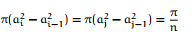

1 function getR2(x, y) { 2 return x * x + y * y; 3 } 4 Array.prototype.BUCKET_SORT = function () { 5 var n = this.length; //n个桶 6 var d2 = 0;//点到(0,0)的距离的平方 7 var num = Math.ceil(d2 * n); //放在第几个桶里。 8 var B = []; //当放桶子用 9 var result = []; 10 for (var i = 0; i < n; i++) { 11 B[i] = {val: [], next: null}; 12 } 13 14 for (var j = 0; j < n; j++) { 15 d2 = getR2(this[j].x, this[j].y); 16 num = Math.ceil(d2 * n); 17 if (num === 0) num++; //直接在原点直接设为第一个桶子里 18 B[num - 1].val.push(this[j]); 19 } 20 21 for (var k = 0; k < n; k++) { 22 if (B[k].val.length == 0) { 23 continue; 24 } 25 B[k].val.INSERT_SORT(); 26 // result.concat(B[k].val); 27 result = result.concat(B[k].val); 28 } 29 return result; 30 }; 31 Array.prototype.INSERT_SORT = function () { 32 for (var i = 1; i < this.length; i++) { 33 var key = this[i]; 34 var j = i - 1; 35 while (j >= 0 && this[j] > key) { 36 this[j + 1] = this[j]; 37 j--; 38 } 39 this[j + 1] = this[i]; 40 } 41 return this; 42 }; 43 44 var A = [{x: 0, y: 0}, {x: 0.21, y: 0.3}, {x: 1, y: 0}]; 45 46 console.log(A.BUCKET_SORT());

