一、题目选择及描述
最大连续子数组和（最大子段和）
问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
二、题目分析
建立一个整型变量temp，用于存储每一次相加得到的子段和，再定义一个整型变量sum用于存储最后结果，并将二者初始值均定义为0。令temp的值等于相邻子数相加的结果，将其与sum的值比较，若temp的值大于sum,则令sum等于temp,否则不变，若temp<0，则将temp置为0，此举是为了保证之前的和小于0，就不计入下一次计算，最终可以得出正确结果
三、代码展示及流程图
1、代码如下
2、流程图如下
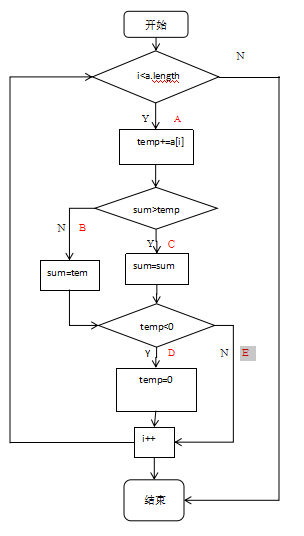
四、覆盖方法的选择
1、组合覆盖方法
要求设计足够多的测试用例，使得每个判定中条件结果的所有可能组合至少出现一次。
2、用例分析
由流程图可知，组合覆盖共有四种情况，分别为ACD，ABD，ABE，ACE。经过分析后可用{-1，4，-5，2}，包含以上所有情况。
3、测试数据运行结果
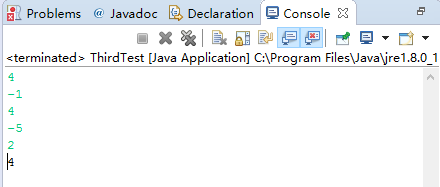
4、数据路径覆盖分析
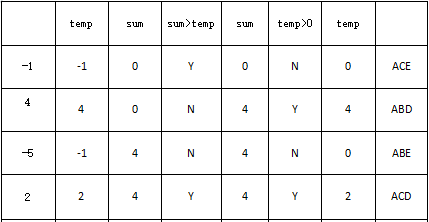
由表可知，此测试数据包含了所有的组合路径。
五、JUnit自动测试
1、代码如下
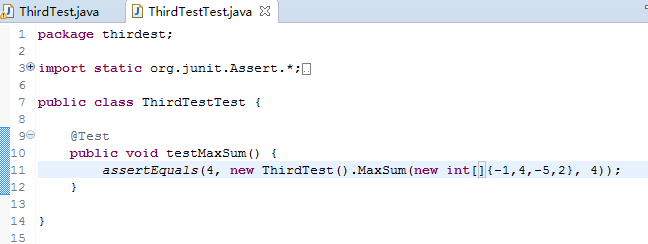
2、测试结果
