Opinion dynamics analysis for stubborn individuals in cooperation–competition networks based on path-dependence framewor
Opinion dynamics analysis for stubborn individuals in cooperation–competition networks based on path-dependence framework[1]
一、Introduction
研究符号网络上一系列相关话题(路径依赖,话题的初始意见是上一个话题的收敛意见)的F-J模型
经典的加权平均模型(DeGroot):
F-J模型:
模型:
,fully stubborn ,partially stubborn ,non-stubborn
路径依赖框架(path-dependence framework)
下面会证明对于每一个话题
s,意见都收敛
将邻居区分为正负邻居且写成矩阵形式
其中
进一步写成
定义
写成矩阵形式,定义
其中
其中
显然矩阵
中间辅助网络
二、预备知识
定义1:对于网络
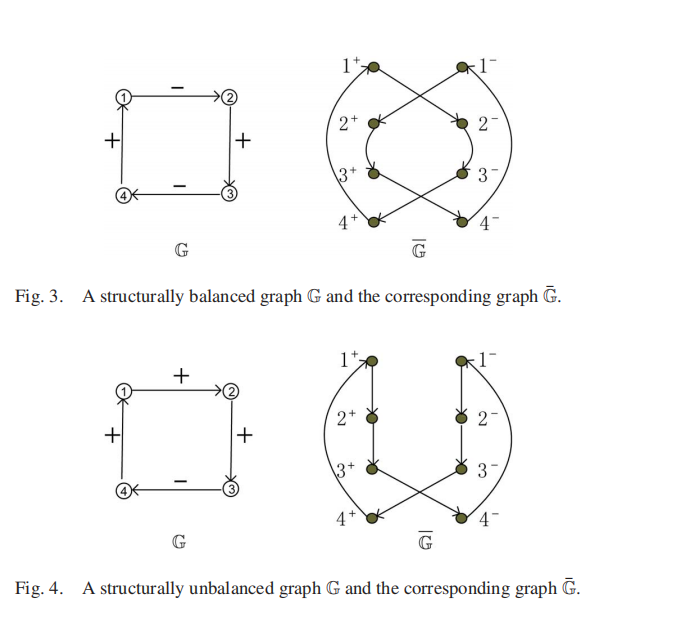
,存在一个节点集合 的划分 。权重矩阵 满足 和 ,则称网络 结构平衡,否则结构不平衡。
引理1:
强连通,则
结构平衡 非强连通,但由两个强连通部分组成
结构不平衡 强连通
在网络
在网络
假设节点划分为
假设
由
假设 1:符号网络
强连通;n个节点,至少存在一个节点部分顽固(partially stubborn, )。
定义 2:模型(2)-(3),如果对任意初始意见
, , 则称节点的意见在话题维度上渐进收敛。
引理:强连通的次随机矩阵谱半径小于1
proof:不失一般性,假设
,由于 是根节点, 即矩阵
行和都小于1, ,又 , ,证毕。
三、主要结论
3.1.
由引理1,
3.1.1. Case 1:不存在完全顽固个体(
(8)式得
从而
Remark 1:定义$\Phi =(I_{2n}-T)^{-1}\cdot\Lambda
\Phi G(T) (I_{2n}-T)^{-1} \Lambda$。
Subcase 1(a):所有个体部分顽固(
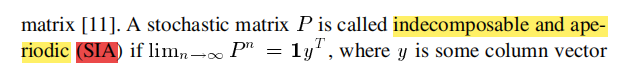
由于
Subcase 1(b):存在
通过转置可得
Remark 2:Case 1情况下,不管是否存在非顽固个体(
),当 意见都渐进收敛到零
3.1.2. Case 2:存在完全顽固个体(
引理 2:
强连通且结构不平衡, 。则 ,特别地, ,存在一条 到 的路径。
显然在网络
不失一般性,假设
由引理2可知,
由引理2可知,对任意的非源节点
记
其中
记
下面引理3给出了
引理 3:
强连通且结构不平衡,完全顽固节点集合 ,则 行随机且 其中
.
下面考虑
取极限
得
进一步考虑
取极限类似可得
递归可得
记
对于Case2,完全顽固节点的意见不变,其他节点的意见收敛于区间
定理 1:考虑模型(2)-(3),网络
强连通且结构不平衡,假设1成立,则
- 如果不存在完全顽固的个体,当话题趋于无穷时,节点意见趋于0。
- 如果存在完全顽固个体
,当话题趋于无穷时,完全顽固个体意见不变,其他节点意见收敛于 。
下面推论1指出,在结构不平衡条件下意见二分一致的充要条件。
推论 1:考虑模型(2)-(3),网络
强连通且结构不平衡,假设1成立。节点意见二分一致当且仅当存在一个唯一的完全顽固的平衡节点,节点 是平衡的指 到 的所有路径符号相等。
充分性:不失一般性,假设节点1是唯一的完全顽固的平衡节点,由引理2,
下证由节点集
假设
case i:存在节点
case ii:存在节点
通过转置变换,矩阵
同理于定理1的Case2的,
必要性:假设意见二分一致。首先证明存在唯一的完全顽固节点,如果不存在完全节点,由定理1的Case1可知意见收敛于零,矛盾;由于完全顽固节点的意见不变,故完全顽固节点的个数小于2。
假设顽固节点1是不平衡的,即存在某个节点
又
递归可得
其中
与意见二分一致矛盾。证毕。
3.2.
定理 2:考虑模型(2)-(3),网络
强连通且结构平衡,假设1成立,则
- 如果不存在完全顽固的个体,当话题趋于无穷时,节点意见二分一致。
- 如果存在完全顽固个体
,当话题趋于无穷时,完全顽固个体意见不变,其他节点意见收敛于 , , ,特别地,如果只有一个完全顽固个体,意见二分一致。
3.3. 动态顽固性
引理 4:
强连通且结构不平衡,在话题 中所有节点都是部分顽固的 。则矩阵 存在,元素都为正,
。
假设 2:对任意的话题
,存在至少一个节点是部分顽固的。存在一个主题子序列 和正整数 ,使得对任意的 满足 , 。
定理 3:考虑模型(32)和(3)。假设
, 强连通和结构不平衡,假设2成立,则意见渐进收敛到零。
对子序列
定义
由于

得
对于任意得
证毕。
对于结构平衡的情况,可以类似得到





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)