一、分类
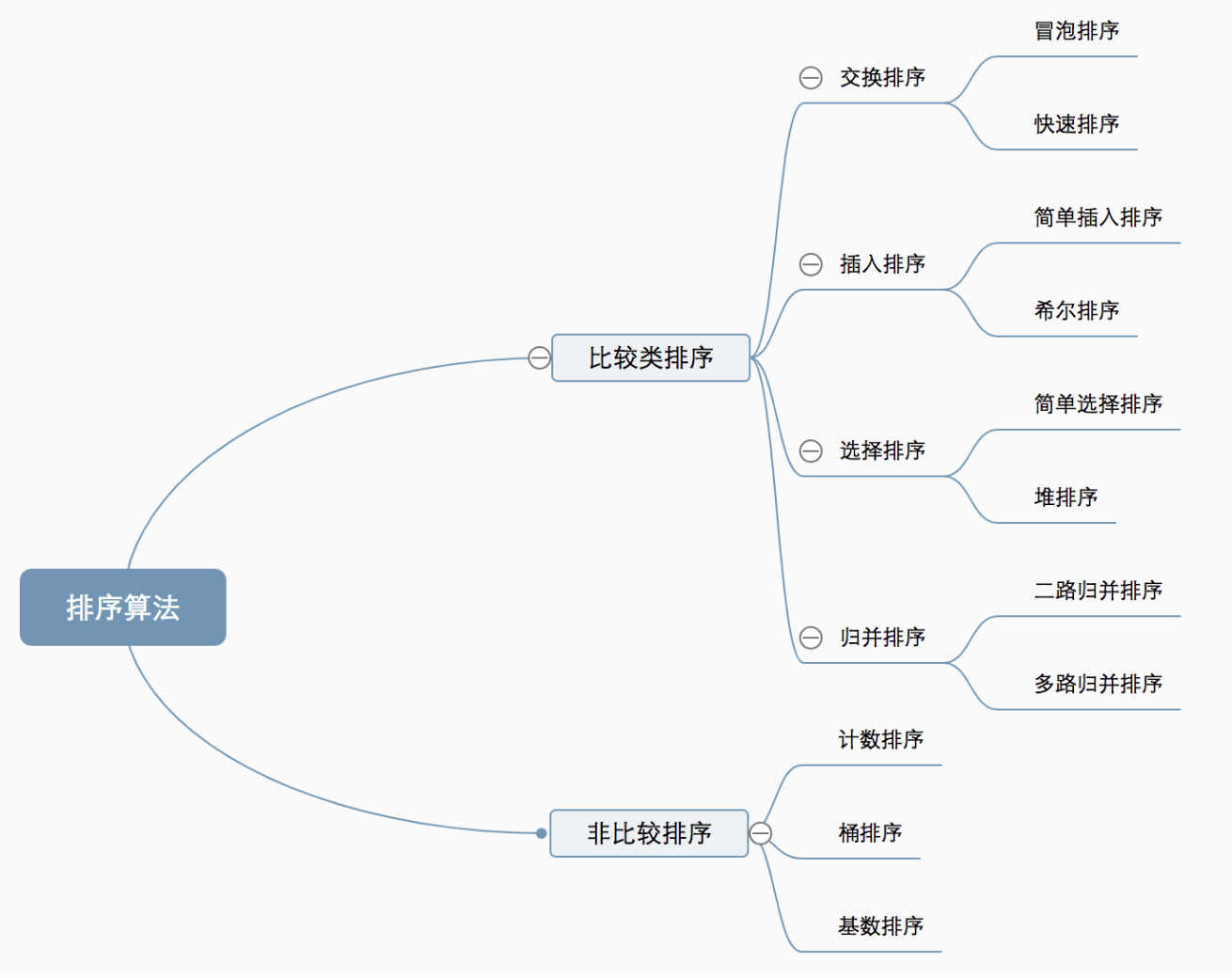
二、时间复杂度
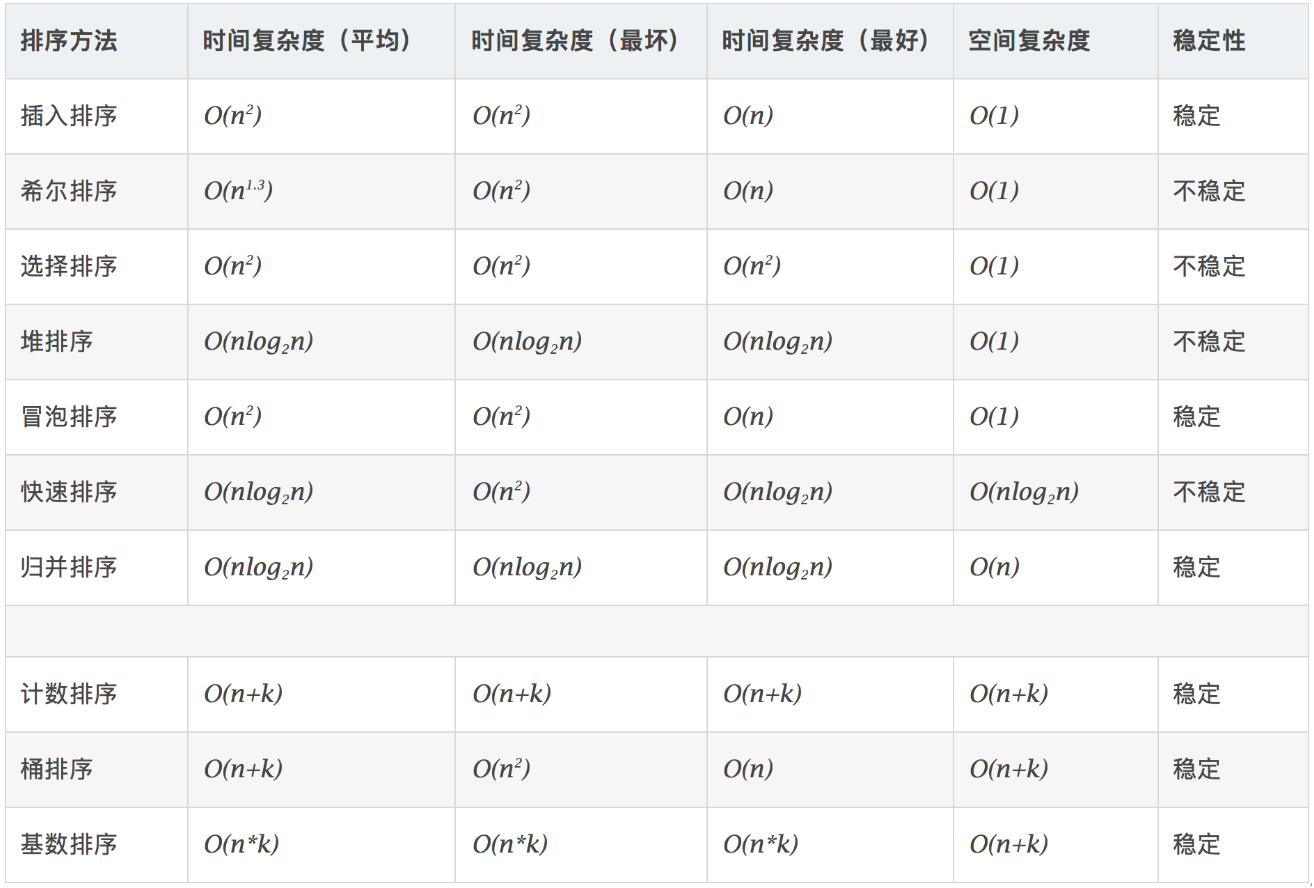
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机
三、算法介绍及java实现(升序)
注意:通过举例子考虑边界
1、选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
选择排序是不稳定的排序方法,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了。
public void xuanze(int[] nums){ for(int i =0;i<nums.length-1;i++){ //最后一位默认有序 int min = i; for(int j=i;j<nums.length;j++){ if(nums[min]>nums[j]) min=j; } int temp = nums[min];//交换排序 nums[min] =nums[i]; nums[i]=temp; } }
2、冒泡排序
每次比较相邻的元素,交换数组,大的值在前面。 时间复杂度由于交换操作多比选择排序高。
稳定。
public void maopao(int[] nums){ for(int i =0;i<nums.length;i++){ for(int j = 0;i<nums.length-i-1;i--){ if(nums[j]>nums[j+1]){ int temp = nums[j]; nums[j]=nums[j+1]; nums[j+1] = temp; }}} }
3、插入排序
插入排序(Insertion sort)是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,算法适用于少量数据的排序,时间复杂度O(n^2)。
稳定
public void charu(int[] nums){ for(int i =1;i<nums.length;i++){ //找到在已排序中的位置 int pos=0; while(nums[pos]<nums[i]){ pos++; } int temp = nums[i]; for(int j= i;j>pos;j--){ nums[j]=nums[j-1]; } nums[pos] =temp; }}
4、希尔排序
第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
gap为增量,每次缩小二分之一的gap,在内部使用插入排序。不稳定。
public void xier(int[] nums){ int gap = nums.length; while(gap>0){ gap/=2; for(int i =0;i<gap;i++){ for(int j =i+gap;j<nums.length;j+=gap){//插入排序 int temp = nums[j]; int k = j - gap; while (k >= 0 && nums[k] > temp) { nums[k + gap] = nums[k]; k -= gap; } nums[k + gap] = temp; } } if(gap==1) break; } }
5、归并排序
稳定。分治法思想,递归实现。
java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。
public static void guibing(int []arr){ int []temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间 sort(arr,0,arr.length-1,temp); } private static void sort(int[] arr,int left,int right,int []temp){ if(left<right){ int mid = (left+right)/2; sort(arr,left,mid,temp);//左边归并排序,使得左子序列有序 sort(arr,mid+1,right,temp);//右边归并排序,使得右子序列有序 merge(arr,left,mid,right,temp);//将两个有序子数组合并操作 } } private static void merge(int[] arr,int left,int mid,int right,int[] temp){ int i = left;//左序列指针 int j = mid+1;//右序列指针 int t = 0;//临时数组指针 while (i<=mid && j<=right){ if(arr[i]<=arr[j]){ temp[t++] = arr[i++]; }else { temp[t++] = arr[j++]; } } while(i<=mid){//将左边剩余元素填充进temp中 temp[t++] = arr[i++]; } while(j<=right){//将右序列剩余元素填充进temp中 temp[t++] = arr[j++]; } t = 0; //将temp中的元素全部拷贝到原数组中 while(left <= right){ arr[left++] = temp[t++]; } }
6、堆排序
不稳定。通过堆结构选择出最大值,后排序
1.找到第一个非叶子节点 i = arr.length/2-1 , 开始遍历所有非叶子节点,调整堆大小,可得到一个最大堆
2.从左至右判断子节点大小,选择出较大的一个,与父节点进行比较交换
3.不断交换堆顶元素和末尾元素(已排序的末尾元素不考虑),排序完成。
public static void dui(int []arr){ //1.构建大顶堆 for(int i=arr.length/2-1;i>=0;i--){ //从第一个非叶子结点从下至上,从右至左调整结构 adjustHeap(arr,i,arr.length); } //2.调整堆结构+交换堆顶元素与末尾元素 for(int j=arr.length-1;j>0;j--){ swap(arr,0,j);//将堆顶元素与末尾元素进行交换 adjustHeap(arr,0,j);//重新对堆进行调整 } } /** * 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上) * @param arr * @param i * @param length */ public static void adjustHeap(int []arr,int i,int length){ int temp = arr[i];//先取出当前元素i for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始 if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点 k++; } if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换) arr[i] = arr[k]; i = k; }else{ break; } } arr[i] = temp;//将temp值放到最终的位置 }
7、快速排序
不稳定。 快速排序(Quicksort)是对冒泡排序的一种改进。
1.以第一个值为基准值,从后往前找到小于基准值的值,复制至前方,开始从前往后找到大于基准值的值,复制至后方。
2.当遍历完成后将基准值复制至最后位置
3.递归基准值左右的数组
public static void kuaipai(int[] arr, int leftIndex, int rightIndex) { if (leftIndex >= rightIndex) { return; } int left = leftIndex; int right = rightIndex; //待排序的第一个元素作为基准值 int key = arr[left]; //从左右两边交替扫描,直到left = right while (left < right) { while (right > left && arr[right] >= key) { //从右往左扫描,找到第一个比基准值小的元素 right--; } //找到这种元素将arr[right]放入arr[left]中 arr[left] = arr[right]; while (left < right && arr[left] <= key) { //从左往右扫描,找到第一个比基准值大的元素 left++; } //找到这种元素将arr[left]放入arr[right]中 arr[right] = arr[left]; } //基准值归位 arr[left] = key; //对基准值左边的元素进行递归排序 kuaipai(arr, leftIndex, left - 1); //对基准值右边的元素进行递归排序。 kuaipai(arr, right + 1, rightIndex); }



