数字信号处理学习笔记——线性卷积直观理解
在信号处理的学习过程中,往往都会学习到,一个信号过一个线性时不变系统,输出的信号即为这个信号与系统的单位冲激响应在时域上线性卷积。最近,有一位好友问我到底为什么与单位冲激响应卷积后就得到了信号过系统的输出,本篇学习笔记将以一个浅显易懂的例子说明这一点。
首先看线性卷积的定义,若要使\(x(n)\)通过一个单位冲激响应为\(h(n)\)的系统,那么其输出的\(y(n)\)则为\(x(n)\ast h(n)\)。
从公式可以看出,卷积就是将序列的翻转、移位、相乘和相加,运算结果称为卷积和。
此时,我们以两个简单的序列卷积为例,解释卷积。
我们另\(x(n)为\{1,1,0,1\}\),另外另系统为\(y(n)=x(n)+x(n-1)+(n-2)\),这个系统的单位冲激响应非常好求,也就是直接把脉冲函数带入\(x(n)\),易得\(h(n)=\delta(n)+\delta(n-1)+\delta(n-2)\),也就是\(h(n)\)为\(\{1,1,1\}\)。
这个系统的物理意义也可以有多种解释,这里给出一个通俗易懂的理解。俗话说,以直报怨,而人的反应就可以理解为一个系统,有输入有输出,我假定你是一个线性时不变的系统,并且\(y(n)=x(n)+x(n-1)+(n-2)\),你的单位冲激响应就为\(\{1,1,1\}\)。
注:matlab绘图中的1时刻即为本文中的零时刻。
那么,我在0时刻打了你一拳,你这个系统就会在0 1 2时刻分别打我一拳,总共打三拳。同时这一响应也就是单位冲激响应。
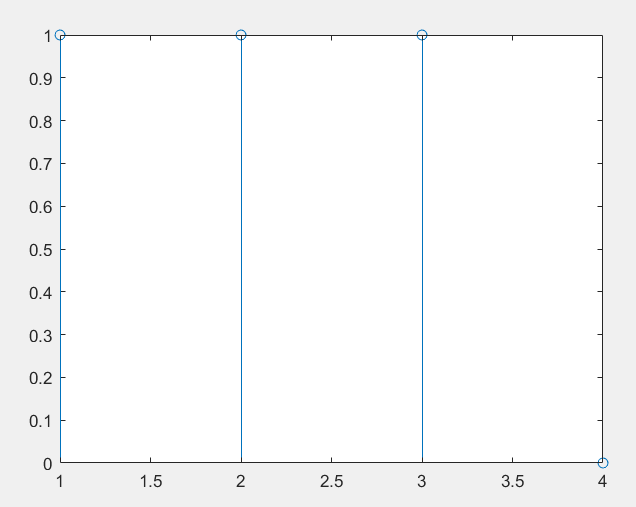
如果我在1时刻又打了你一拳,那么按照你线性时不变的性质,你就会在1 2 3时刻又分别打我一拳。

你就会发现,叠加上时刻0时的响应,你在1和2时刻会打我两拳,0和3时刻则是一拳。
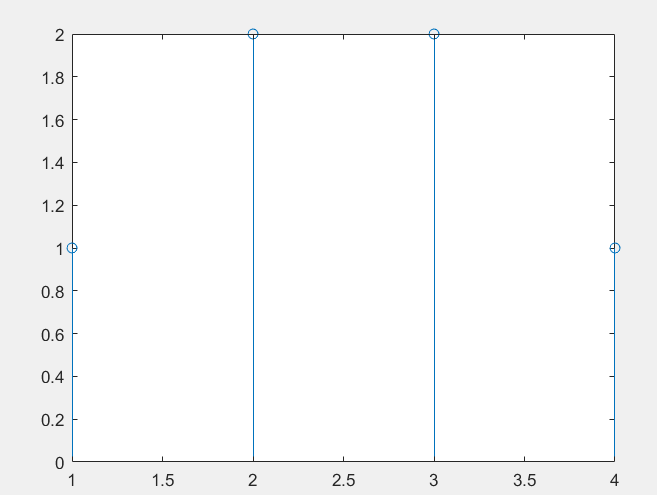
而我在时刻2没有出拳,你也不会有响应。我在3时刻又出拳了,那么你又会在3 4 5时刻分别打我一拳。

那么,我按照{1,1,0,1}\(,几个不同时刻你的响应相互之间叠加。你从零时刻开始,对我出拳即为输出\)y(n)\(,为\){1,2,2,2,1,1}$。

同样,如果输入的强度有所变化,我在一个时刻打你两拳,你也会在此时刻以及后面两个时刻上分别打我两拳。
因此,我们将输入序列翻转、移位,可以看作使序列按照时间顺序输入系统中。相乘体现不同时刻的输入强度,相加则是将不同时刻的输入得到的响应求和。

一样能够得到:




