CF938G Shortest Path Queries(线性基+线段树分治)
CF938G Shortest Path Queries
出现了!融合怪!
其实这题就是这两题融合一下
我们来讲解法。首先我们看到了这个 XOR 的最小值问题,可以借鉴最大XOR和路径这道题的思路。其次我们有删边,加边的操作,可以用线段树分治的思路。但是很显然,这中间还有很多有待思考的问题。比如,如何实现线性基撤销?怎样合并边,并维护线性基?我们来一一攻破。
线性基撤销
这个我是没怎么好好想过,反正我是对于每个线段树上的节点都建了一个线性基,每次下传即可。挺暴力的,但是空间可以卡过的。
边的合并
我们可以这样想。如果此时两个点不在一个连通块里,我们可以在这两条边之间加一条边。但是这个违反了并查集的规则。并查集只能将两个集合的根节点合并。我们就需要用到二分图中的一个思路。比如说,如下图:
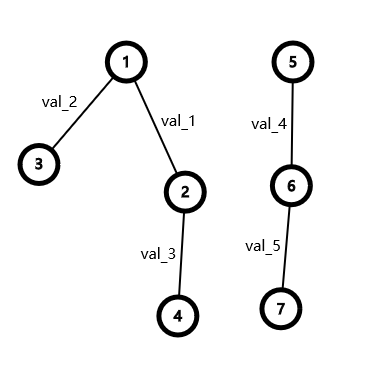
(由于绘图不支持 \(\LaTeX\),所以下划线就标在那里了,不是图炸了)
我们现在要在 \(2\) 和 \(6\) 之间添一条边,权值为 \(val_6\)。我们应该得到下图:
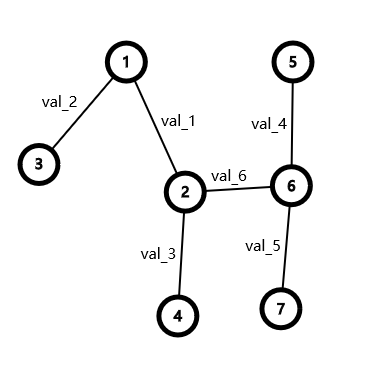
但是实际上我们不能这么做,我们的并查集只支持根节点合并。那么怎么办?我们令节点 \(i\) 到它所属的并查集的根的距离为 \(dis_i\)。那么若我们连接 \(u,v\) 两点,权值为 \(w\),我们就相当于在这两个点分别所属的并查集的根节点连一条权值为 \(dis_u \operatorname{xor} dis_v \operatorname{xor} w\) 的边。比如对于我们举的例子,就是这个效果:
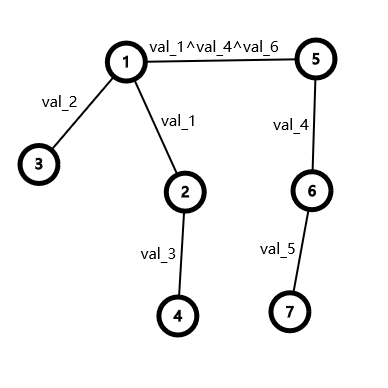
这为什么是对的呢?其实就是运用了 \(x\operatorname{xor} x=0\) 的性质。我们举几个例子,比如对于原图,\(3->6\) 的路径权值为 \(val_2\operatorname{xor}val_1\operatorname{xor} val_6\)。而现在是 \(val_2\operatorname{xor}\ (val_1\operatorname{xor}val_4\operatorname{val_6})\operatorname{val_4}\)。居然是一样的。
如果连的边两个端点本来就在一个连通块里,就把环扔到线性基里,和 WC 那题一样。
好了,然后就到了写代码时间。。。。
反正我写了 208 行,调了 4 天,结果发现数组开小了。。。
参考代码:
//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
#define pr pair<int,int>
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int MAXN=2e5+10;
int n,m,q,cnt;
int father[MAXN],dis[MAXN],size[MAXN],lb[MAXN<<2][32];
struct ege {
int u,v,w;
}e[MAXN<<1];
map<pr,int> mp,index;
set<int> s;
vector<ege> edge[MAXN<<2];
vector<pr > qry[MAXN<<2];
stack<pr > stk;
pr make_edge(int x,int y) {
return make_pair(min(x,y),max(x,y));
}
void insert(int x,int p) {
for(int i=30;i>=0;i--) {
if(x&(1<<i)) {
if(lb[p][i]) {
x^=lb[p][i];
}
else {
lb[p][i]=x;
return ;
}
}
}
}
int find(int x) {
if(x!=father[x]) {
return find(father[x]);
}
return x;
}
int findis(int x) {
if(x!=father[x]) {
return dis[x]^findis(father[x]);
}
return 0;
}
void merge(ege s,int p) {
int x=find(s.u);
int y=find(s.v);
if(x==y) {
insert(findis(s.u)^findis(s.v)^s.w,p);
stk.push(make_pair(-1,-1));
return ;
}
if(size[x]>size[y]) {
swap(x,y);
}
dis[x]=findis(s.u)^findis(s.v)^s.w;
father[x]=y;
size[y]+=size[x];
stk.push(make_pair(x,y));
}
void del() {
int x=stk.top().first;
int y=stk.top().second;
stk.pop();
if(x==-1) {
return ;
}
father[x]=x;
dis[x]=0;
size[y]-=size[x];
}
void modify(int l,int r,int p,int x,int y,ege s) {
if(x>y||r<x||y<l) {
return ;
}
if(x<=l&&r<=y) {
edge[p].push_back(s);
return ;
}
int mid=(l+r)>>1;
modify(l,mid,p<<1,x,y,s);
modify(mid+1,r,p<<1|1,x,y,s);
}
void modqry(int l,int r,int p,int x,int y,pr s) {
if(x>y||r<x||y<l) {
return ;
}
if(x<=l&&r<=y) {
qry[p].push_back(s);
return ;
}
int mid=(l+r)>>1;
modqry(l,mid,p<<1,x,y,s);
modqry(mid+1,r,p<<1|1,x,y,s);
}
void query(int l,int r,int p) {
int sz=edge[p].size();
for(int i=0;i<sz;i++) {
merge(edge[p][i],p);
}
if(l==r) {
int qsz=qry[p].size();
for(int i=0;i<qsz;i++) {
int ans=0;
if(find(qry[p][i].first)!=find(qry[p][i].second)) {
printf("0\n");
break;
}
ans=findis(qry[p][i].first)^findis(qry[p][i].second);
for(int j=30;j>=0;j--) {
ans=min(ans,ans^lb[p][j]);
}
printf("%lld\n",ans);
}
}
else {
int mid=(l+r)>>1;
for(int i=0;i<=30;i++) {
lb[p<<1][i]=lb[p][i];
lb[p<<1|1][i]=lb[p][i];
}
query(l,mid,p<<1);
query(mid+1,r,p<<1|1);
}
while(sz--) {
del();
}
}
signed main() {
cin>>n>>m;
for(int i=1;i<=n;i++) {
father[i]=i;
size[i]=1;
dis[i]=0;
}
for(int i=1;i<=m;i++) {
e[i].u=read();e[i].v=read();e[i].w=read();
pr tmp=make_edge(e[i].u,e[i].v);
s.insert(i);
mp[tmp]=1;
index[tmp]=i;
}
cnt=m;
cin>>q;
for(int i=1;i<=q;i++) {
int opt,u,v,w;
opt=read();u=read();v=read();
if(opt==1) {
w=read();
pr tmp=make_edge(u,v);
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].w=w;
s.insert(cnt);
mp[tmp]=i;
index[tmp]=cnt;
}
if(opt==2) {
pr tmp=make_edge(u,v);
modify(1,q,1,mp[tmp],i-1,e[index[tmp]]);
s.erase(s.find(index[tmp]));
mp[tmp]=index[tmp]=0;
}
if(opt==3) {
modqry(1,q,1,i,i,make_edge(u,v));
}
}
for(set<int>::iterator it=s.begin();it!=s.end();it++) {
modify(1,q,1,mp[make_edge(e[(*it)].u,e[*it].v)],q,e[*it]);
}
query(1,q,1);
return 0;
}
/*
5 6
1 2 31
1 5 0
2 3 30
2 4 0
3 4 1
3 5 30
5
2 2 3
2 2 4
1 2 3 1
1 2 4 1
3 1 2
5 6
1 2 31
1 5 0
2 3 30
2 4 0
3 4 1
3 5 30
8
3 1 2
2 3 5
1 3 5 30
2 2 3
2 2 4
1 2 3 1
1 2 4 1
3 1 2
*/


