CF845G Shortest Path Problem?（线性基）

CF845G Shortest Path Problem?

裸的线性基，只不过需要一些变化。

我们首先需要对图构建一颗随意的生成树。只要是颗树即可。比如说我们构造出了如下的一张图（其中边权为 .... 的代表这之间可能省略了一些边）：

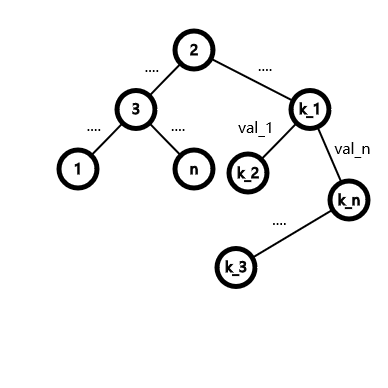
我们可以通过一次 DFS 求出每个点到根节点，即 \(2\) 号点，的距离 \(dis_i\)。注意根节点不一定是 \(2\)，最好不要是 \(1\) 或 \(n\)，没试过是否可以。

显然我们还有一些不在生成树里的边，对于这些边，有一个废话一样的性质，就是他们加进图去后，至少会产生一个新的环。比如说我们加入一条边 \((k_2,k_3)\)，得到图：

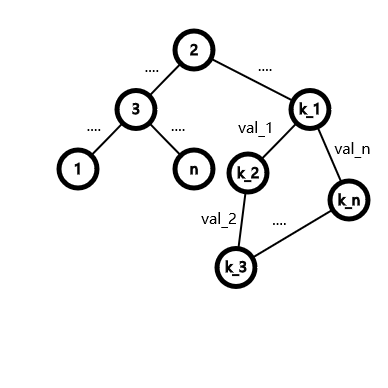
我们得到了一个环 \(k_1,k_2,k_3,\cdots,k_n\)，环的权值是 \(val_c=val_1 \operatorname{xor} val_2\operatorname{xor} val_3\cdots\operatorname{xor} val_n\)。我们的 \(1->n\) 的路径上如果要经过这个环怎么办呢？我们可以这样想，其实我们遍历一下这个环得到的权值是 \(dis_1 \operatorname{xor} dis_{k_1} \operatorname{xor} val_c \operatorname{xor} dis_{k_1} \operatorname{xor} dis_1=val_c\)。因此只是把这个环的权值加了进去。

由于任意一个环都可以用几个环异或出来，我们只需要把每条新加入的边形成的环加到线性基里，求出最小值后，再异或上必须要有的 \(dis_1\) 和 \(dis_n\)，就是答案。

时间复杂度 \(O(n)\)。

//Don't act like a loser.
//This code is written by huayucaiji
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;

int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}

const int MAXN=2e5+10;

int n,m,cnt;
int p[100],h[MAXN],father[MAXN],dis[MAXN];

int find(int x) {
	if(x!=father[x]) {
		return father[x]=find(father[x]);
	}
	return father[x];
}

void insert(int x) {
	for(int i=63;i>=0;i--) {
		if(!(x&(1ll<<i))) {
			continue;
		}
		if(!p[i]) {
			p[i]=x;
			break;
		}
		x=p[i]^x;
	}
}

struct edge {
	int u,v,w,next;
	bool tree;
}e[MAXN<<2];

void addedge(int u,int v,int w) {
	e[++cnt].u=u;
	e[cnt].v=v;
	e[cnt].w=w;
	e[cnt].next=h[u];
	h[u]=cnt;
}

void generate_tree() {
	for(int i=1;i<=m;i++) {
		if(find(e[i].u)!=find(e[i].v)) {
			father[find(e[i].u)]=find(e[i].v);
			e[i].tree=1;
			e[i+1].tree=1;
		}
	}
}
void dfs(int u,int fa) {
	for(int i=h[u];i;i=e[i].next) {
		if(!e[i].tree) {
			continue;
		}
		int v=e[i].v;
		
		if(v!=fa) {
			dis[v]=dis[u]^e[i].w;
			dfs(v,u);
		}
	}
}

signed main() {
	cin>>n>>m;
	for(int i=1;i<=n;i++) {
		father[i]=i;
	}
	for(int i=1;i<=m;i++) {
		int u,v,w;
		u=read();
		v=read();
		w=read();
		addedge(u,v,w);
		addedge(v,u,w);
	}
	m<<=1;
	
	generate_tree();
	dfs(2,0);
	
	for(int i=1;i<=m;i++) {
		if(!e[i].tree) {
			insert(dis[e[i].u]^dis[e[i].v]^e[i].w);
		}
	}
	
	int ans=dis[1]^dis[n];
	for(int i=63;i>=0;i--) {
		ans=min(ans,ans^p[i]);
	}
	
	cout<<ans<<endl;
	return 0;
}