Codeforces Round 662 赛后解题报告(A-E2)
Codeforces Round 662 赛后解题报告
梦幻开局到1400+的悲惨故事
A. Rainbow Dash, Fluttershy and Chess Coloring
这个题很简单,我们可以画几张图,发现每一次我们染色的最佳方法就是每次往里面多填一圈,并把上一圈给填满。
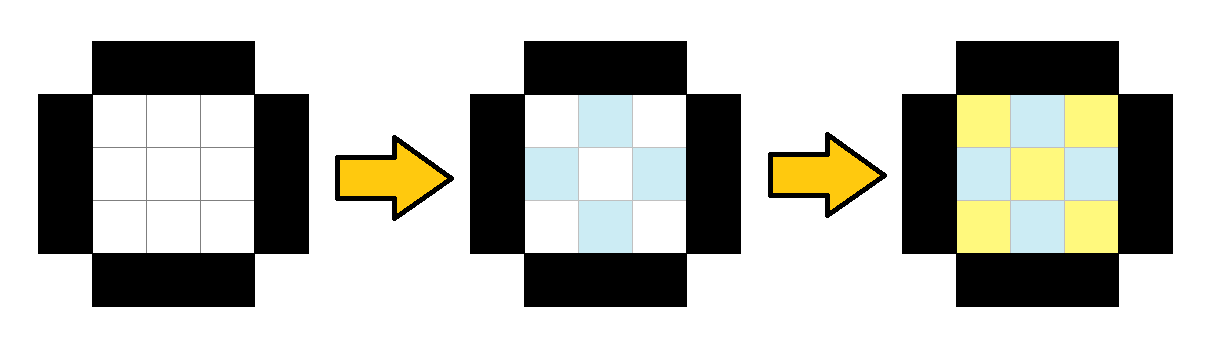
比如上图就很好地说明了这个过程,大家可以用画一下 \(n=4,n=5,n=6,n=7\),就能验证这个命题了,所以一个 \(n\times n\) 的矩阵有 \(\lfloor\frac{n}{2}\rfloor+1\) 圈,所以直接输出即可。
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
//#pragma GCC optimize("Ofast","-funroll-loops","-fdelete-null-pointer-checks")
//#pragma GCC target("ssse3","sse3","sse2","sse","avx2","avx")
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n;
signed main() {
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
int t=read();
while(t--) {
n=read();
cout<<n/2+1<<endl;
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
B. Applejack and Storages
我们思考一下这个题给我们的信息。我们要用已有木棒拼出一个正方形和一个长方形。因为长方形的范围比正方形广,所以我们有一个贪心策略就是先判断是否有正方形再判断剩下的是否有长方形。
我们做的就是要统计有多少组木棒可以拼出正方形,我们记为 \(four\)(重复的木棒不能出现在两组中)。我们再来统计把所有 \(4\) 个木棒长度相等的组剔除后,有多少组是两个木棒程度相等的,记为 \(two\)。注意,由于我们的贪心策略,我们优先考虑 \(four\)。所以两组相等的二元组就会被我们合并成为一个四元组。
最后只要满足 \(four>0\) 且 \(two>1\),或者 \(four>1\),即拼出两个正方形,我们就输出 YES。否则 NO。
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int maxn=1e5+10;
int n,cnt[maxn],m,four,two;
char ch;
signed main() {
n=read();
for(int i=1;i<=n;i++) {
int x=read();
cnt[x]++;
if(cnt[x]%4==0) {//先4后2
four++;
two--;
}
if(cnt[x]%4==2) {
two++;
}
}
m=read();
for(int i=1;i<=m;i++) {
cin>>ch;
int x=read();
if(ch=='+') {
cnt[x]++;
if(cnt[x]%4==0) {//先4后2
four++;
two--;
}
if(cnt[x]%4==2) {
two++;
}
}
else {
if(cnt[x]%4==0) {//先4后2
four--;
two++;
}
if(cnt[x]%4==2) {
two--;
}
cnt[x]--;
}
if(four>0&&two>1) {
printf("Yes\n");
}
else if(four>1) {
printf("YES\n");
}
else {
printf("NO\n");
}
}
return 0;
}
C. Pinkie Pie Eats Patty-cakes
此题的数学方法不再赘述,我们来关注一下冷门的二分答案(至少我没看到几个二分答案做的)。
确定做法二分答案,我们的重点就放在了 check 函数上。首先先讲讲我在考试的时候怎么想的(这个是错误想法)。
我们确定了一个答案 \(x\),判断是否可行,我们一个一个放数字,从出现次数最多的开始放,每隔 \(x\) 个位置就放一个,如果已经到头了,却还有剩余,就代表答案不存在,返回 \(0\)。但这是错的。我们举个例子,比如对于:
10
4 4 4 4 3 3 2 2 1 1
按照我们的做法,若 \(x=2\),放完了 \(4,3,2\) 后,是这样的一个序列:\(4\ 3\ 2\ 4\ 3\ 2\ 4\ 0\ 0\ 4\)。其中 \(0\) 代表还未放置的数。明显,我们会认为它是不可行的。其实我们可以实现,比如这个序列:\(4\ 3\ 2\ 4\ 1\ 2\ 4\ 1\ 3\ 4\)。这个check直接暴毙。
我们来换一个贪心的思路。我们考虑到第 \(i\) 个位置,若在 \([i-x-1,i]\) 内 \(k\) 这个数还没有出现过,那么 \(k\) 就成为了 \(i\) 这个位置上的候选人。假设我们有 \(d\) 个候选人 \(k_1,k_2...k_d\)。我们就肯定先选择剩下还需在序列中出现次数最多的那个数,填在 \(i\) 这个位置上。因为填在这一位上,肯定比在 \(i+q\) 的位置上优。如果在考虑某个位置时,没有可以选择的数,即 \(d=0\) 时,肯定是无解的,返回 \(0\)。在计算时用一个堆维护即可。时间复杂度为 \(O(n\log^2 n)\)。可以卡过此题。
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int maxn=1e5+10;
int n,a[maxn],cnt[maxn];
int b[maxn];
bool check(int x) {
fill(b+1,b+n+1,0);
priority_queue<pair<int,int> > q;
for(int i=1;i<=n;i++) {
if(cnt[i])
q.push(make_pair(cnt[i],i));
}
for(int i=1;i<=n;i++) {
if(i>x+1) {
if(cnt[b[i-x-1]])
q.push(make_pair(cnt[b[i-x-1]],b[i-x-1]));//把重新“合法”的这个数加回堆中。
}
if(q.empty()) {
return 0;//此时无解
}
pair<int,int> pr=q.top();
q.pop();
cnt[pr.second]--;//剩余出现次数减1
b[i]=pr.second;
}
return 1;
}
void clear() {
fill(cnt+1,cnt+n+1,0);
for(int i=1;i<=n;i++) {
cnt[a[i]]++;
}
}
signed main() {
int t=read();
while(t--) {
n=read();
for(int i=1;i<=n;i++) {
a[i]=read();
cnt[a[i]]++;
}
int l=0,r=n-2;
while(l+1<r) {
int mid=(l+r)>>1;
clear();//恢复cnt数组
if(check(mid)) {
l=mid;
}
else {
r=mid;
}
}
clear();//恢复cnt数组
if(check(r)) {
printf("%d\n",r);
}
else {
printf("%d\n",l);
}
fill(cnt+1,cnt+n+1,0);
}
return 0;
}
D. Rarity and New Dress
首先我们可以转化一下问题,我们先令一个满足衣服图案的区域的几何中心为这个衣服的中心,我们再令以 \((x,y)\) 为中心的最大的衣服的半径为 \(r_{x,y}\)。那么我们的答案就为:
对于半径我们结合图再来规定一下。对于下图(来自题目):
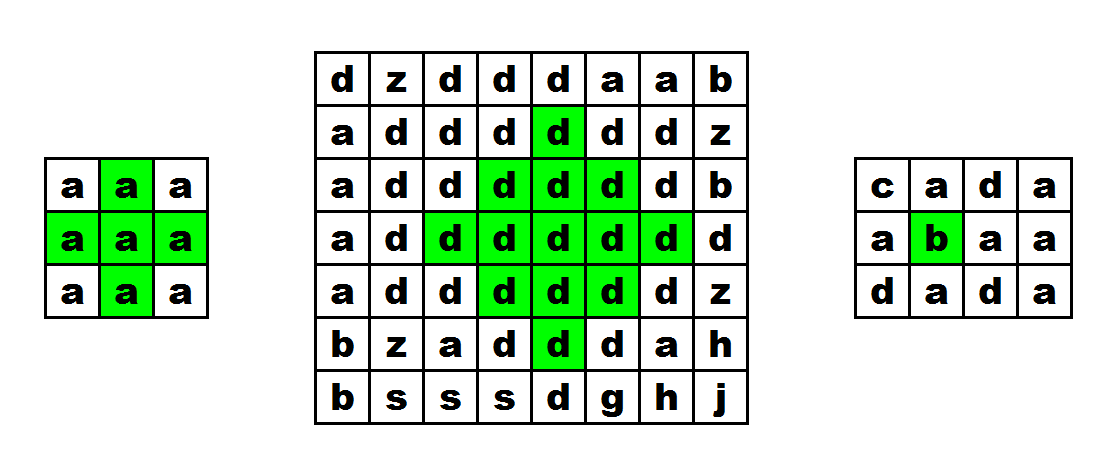
比如对于第一张图(左一),我们的半径为 \(1\);中间的那幅,半径为 \(2\);最右边的半径为 \(0\)。
我们来具体分析如何求解。
我们如果把这个图形分成左右两半,我们会发现都是一个金字塔的形状,且从上往下宽度以 \(2\) 为公差递增。这就是我们解决问题的切入点,分别取统计两边的金字塔大小,两边取 \(\min\),即为半径大小。但是怎么求金字塔大小?以左边为例我们先来求以 \((x,y)\) 为中心的上下方向的线段的最大长度,记为 \(len_{x,y}\)。然后我们再令 \((x,y)\) 左边的最大金字塔的长度为 \(left_{x,y}\)。则我们有 \(left_{x,y}=\min(\lfloor\frac{len_{x,y}}2\rfloor,left_{x,y-1}+1)\)。右边同理。这个问题就解决了。
顺便提一句:记得用 getchar(),否则会被卡常。博主亲测过得哟,亲。
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int maxn=2000+10;
int n,m,u[maxn][maxn],l[maxn][maxn],r[maxn][maxn],d[maxn][maxn],len[maxn][maxn];
char c[maxn][maxn];
signed main() {
n=read();m=read();
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
c[i][j]=getchar();
}
c[0][0]=getchar();
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(c[i][j]==c[i-1][j]) {
u[i][j]=u[i-1][j]+1;
}
}
}
for(int i=n;i>0;i--) {
for(int j=1;j<=m;j++) {
if(c[i][j]==c[i+1][j]) {
d[i][j]=d[i+1][j]+1;
}
len[i][j]=1+min(d[i][j],u[i][j])*2;
}
}
for(int i=1;i<=n;i++) {
for(int j=0;j<=m;j++) {
if(c[i][j]==c[i][j-1]) {
l[i][j]=min(len[i][j]/2,l[i][j-1]+1);
}
}
}
int ans=0;
for(int i=1;i<=n;i++) {
for(int j=m;j>0;j--) {
if(c[i][j]==c[i][j+1]) {
r[i][j]=min(len[i][j]/2,r[i][j+1]+1);
}
ans+=min(l[i][j],r[i][j])+1;
}
}
cout<<ans<<endl;
return 0;
}
E1. Twilight and Ancient Scroll (easier version)
这个题我们一步一步地来优化时间和空间复杂度。
注意,本题中字符串的下标从 \(0\) 开始
我们令第 \(i\) 个字符串为 \(str_i\),其长度为 \(len_i\)。
时间:\(O(L^3)\),空间:\(O(nL)\)
我们看到这个题很快可以想到是 DP,所以我们先来列个状态。我们令 \(f_{i,j}\) 为考虑到第 \(i\) 个字符串,这个字符串删除第 \(j\) 个字符,保证前 \(i\) 个字符串是按字典序排列的方案数是多少。可是我们很快遇到了一个棘手的问题:如果这个字符串我选择不删除任何字符怎么办?这个时候我们可以采取在字符串末尾加一个'#'符号,如果我们不删字符,我们就选择删这个字符。由于'#'比26个小写字母的ASCII编码小,也自动解决了长度的问题。我们再回过头看 DP,我们有转移方程:\(f_{i,j}=\sum\limits_{k=0,满足字典序要求}^{len_i} f_{i-1,k}\)。我们最后的答案就是 \(\sum\limits_{j=0}^{len_i} f_{n,j}\)。这是最朴素的 DP,还是很好想的。
时间:\(O(L^2\log L)\),空间:\(O(nL)\)
我们来进一步优化这个 DP。我们发现如果我们对第 \(i\) 个字符串把每个位置上的字符删掉会得到 \(len_i\) 个新字符串。如果我们对这些字符串排序。在 DP 的时候就可以用 \(\operatorname{upperbound}\) 来利用字符串单调性来优化了。但此时我们还需要改一下 \(f_{i,j}\) 的定义。如果我们令排好序后删除了第 \(i\) 个字符的那个新字符串排名为 \(rnk_i\)。我们再定义一个数组 \(place_i\),意义为排名为 \(i\) 的字符是原字符串中的第 \(palce_i\) 个,所以满足\(rnk_{palce_i}=i\)。我们的\(f_{i,j}\) 改为考虑到第 \(i\) 个字符串,这个字符串删除第 \(place_j\) 个字符,保证前 \(i\) 个字符串是按字典序排列的方案数是多少。显然我们的转移方程要发生改变,但大体与上面的一样,这里不再赘述(因为表达比较烦,具体可以看程序)。排序 \(O(L^2\log L)\),DP时间复杂度 \(O(L^2\log L)\)。空间复杂度还是为 \(O(nL)\)。
时间:\(O(L\log^2 L)\),空间:\(O(2L)\)
我们再来优化一下。我们来分析一下之前时间复杂度的分布,排序可以认为是 \(O(L\log L)\times O(L)\),\(O(L)\) 是字符串比大小的时间。而 DP 中是 \(O(L)\times O(\log L)\times O(L)\) 第一个是状态总数,第二个是二分查找(\(\operatorname{upperbound}\))的时间。最后一个是字符串比大小。因此我们发现这里唯一可以优化的就是字符串比大小。我们很容易想到细节贼多的Hash+二分,把字符串比较的时间降为 \(O(\log L)\)。最后时间复杂度为 \(O(L\log^2 L)\)。我们转移 \(f_{i,j}\),只需要 \(f_{i-1,k}\) 的信息,因此可以滚动数组来优化空间,空间复杂度为 \(O(2L)\)。此题可以通过。
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
#define int long long
using namespace std;
int read() {
char ch=getchar();
int f=1,x=0;
while(ch<'0'||ch>'9') {
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
const int P[2]={33,37},MOD[2]={20060527,21071179},MAXN=1e3+10,ANSMOD=1e9+7;
int n,f[2][MAXN*20],p[2][MAXN*20];
int sum[2][MAXN*20]={};
vector<pair<int,int> > myhsh[MAXN];
string str[MAXN];
void myhsh_generator(int x) {
int ret[2]={};
int sz=str[x].size();
for(int i=0;i<sz;i++) {
for(int j=0;j<=1;j++) {
ret[j]=(ret[j]*P[j]%MOD[j]+(int)str[x][i])%MOD[j];
}
myhsh[x].push_back(make_pair(ret[0],ret[1]));
}
}
pair<int,int> consecutive_myhsh_query(int x,int l,int r) {
if(l>r) {
return make_pair(0,0);
}
pair<int,int> ret=make_pair(myhsh[x][r].first,myhsh[x][r].second);
if(l!=0) {
ret.first=(ret.first-p[0][r-l+1]*myhsh[x][l-1].first%MOD[0]+MOD[0])%MOD[0];
ret.second=(ret.second-p[1][r-l+1]*myhsh[x][l-1].second%MOD[1]+MOD[1])%MOD[1];
}
return ret;
}
pair<int,int> myhsh_query(int x,int l,int r,int del) {
int sz=str[x].size();
if(del<=l) {
l++;
}
if(del<=r) {
r++;
}
l=min(sz-1,l);
r=min(sz-1,r);
if(l<=del&&del<=r) {
pair<int,int> left=consecutive_myhsh_query(x,l,del-1);
pair<int,int> right=consecutive_myhsh_query(x,del+1,r);
pair<int,int> ret=make_pair(0,0);
ret.first=(left.first*p[0][max(r-del,0LL)]%MOD[0]+right.first)%MOD[0];
ret.second=(left.second*p[1][max(r-del,0LL)]%MOD[1]+right.second)%MOD[1];
return ret;
}
return consecutive_myhsh_query(x,l,r);
}
bool compare(int x,int delx,int y,int dely) {
int len1=str[x].size();
int len2=str[y].size();
if(delx!=len1) len1--;
if(dely!=len2) len2--;
int l=0,r=min(len1,len2)-2;
while(l<r) {
int mid=(l+r)>>1;
if(myhsh_query(x,l,mid,delx)==myhsh_query(y,l,mid,dely)) {
l=mid+1;
}
else {
r=mid;
}
}
if(myhsh_query(x,l,l,delx)!=myhsh_query(y,l,l,dely)) {
return myhsh_query(x,l,l,delx)<myhsh_query(y,l,l,dely);
}
return len1<len2;
}
struct strpair {
int del,id;
bool operator <(const strpair& a)const {
return compare(id,del,a.id,a.del);
}
};
strpair make_strpair(int x,int y) {
strpair ret;
ret.del=x;
ret.id=y;
return ret;
}
vector<strpair> s[MAXN];
signed main() {
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=read();
/*if(n==800) {
printf("40399797");
return 0;
}*/
p[0][0]=1;p[1][0]=1;
for(int i=1;i<=20000;i++) {
p[0][i]=p[0][i-1]*P[0]%MOD[0];
p[1][i]=p[1][i-1]*P[1]%MOD[1];
}
for(int i=1;i<=n;i++) {
cin>>str[i];
str[i]=str[i]+'$';
myhsh_generator(i);
int sz=str[i].size();
for(int j=0;j<sz;j++) {
s[i].push_back(make_strpair(j,i));
}
sort(s[i].begin(),s[i].end());
/*printf("\n");
for(vector<strpair>::iterator j=s[i].begin();j!=s[i].end();j++) {
for(int k=0;k<sz;k++) {
if(k!=(*j).del) {
cout<<str[i][k];
}
}
printf("\n");
}
printf("\n");*/
}
for(int i=1;i<=n;i++) {
int sz=str[i].size();
for(int t=0;t<sz;t++) {
int j=s[i][t].del;
if(i==1) {
f[i%2][t]=1;
}
else {
int k=upper_bound(s[i-1].begin(),s[i-1].end(),make_strpair(j,i))-s[i-1].begin();
if(k>0) {
f[i%2][t]=sum[(i-1)%2][k-1];
}
else {
f[i%2][t]=0;
}
}
}
for(int t=0;t<sz;t++) {
sum[i%2][t]=((t==0? 0:sum[i%2][t-1])+f[i%2][t])%ANSMOD;
}
}
cout<<sum[n%2][s[n].size()-1]<<endl;
//fclose(stdin);
//fclose(stdout);
return 0;
}
E2. Twilight and Ancient Scroll (harder version)
本题需要建立在理解Easier Version 的基础上才能理解,请先阅读Easier Vesion的题解。
我们的时间复杂度大户是排序和DP,我们来分别优化这两个部分。
优化DP
这个地方其实很好想,我们排好序后的字符串是有序的,那么我们用二分查找(\(\operatorname{upperbound}\))查出来的结果 \(k\) 是单调递增的。所以我们可以用两个指针维护住 \(k\) 和当前字符串的次序,使得时间复杂度变为 \(O(L\log L)\),符合要求。
优化排序
我们发现其实在排序的时候两个字符串只有两个字符不同,也就是删去的两个字符。因此我们可以简化排序。我们令字符串中在第 \(i\) 个字符右边的第一个与第 \(i\) 个字符不同的字符的下标为 \(nxt_i\)(有点绕没办法,本人语文不好)。我们只要观察这两个字符的大小即可知道删去第 \(i\) 个字符的字符串排序后所在的位置。我们维护 \(l,r\) 代表当前字符串所在位置的可能候选人。如果 \(str_i>str_{nxt_i}\),那么删去第 \(i\) 个字符的字符串排在第 \(l\) 个位置。否则放在第 \(r\) 个位置。我们来证明一下。
我们只证明如果 \(str_i>str_{nxt_i}\),那么删去第 \(i\) 个字符的字符串排在第 \(l\) 个位置。反之证明亦然。
首先我们通过 \(nxt_i\) 的定义可知,\([i,nxt_i-1]\) 区间内的字符都相等。那么删去了第 \(i\) 个字符的字符串和删去了第 \(nxt_i+q\ (nxt_i+q<len,q\geq 0)\) 个字符的字符串对比如下表:
| \(i\) | \(i+1\) | \(i+2\) | .... | \(nxt_i-1\) | |
|---|---|---|---|---|---|
| 删去了第 \(i\) 个字符的字符串 | \(str_{i+1}\) | \(str_{i+2}\) | \(str_{i+3}\) | .... | \(str_{nxt_i}\) |
| 删去了第 \(nxt_i+q\) 个字符的字符串 | \(str_{i}\) | \(str_{i+1}\) | \(str_{i+2}\) | .... | \(str_{nxt_i-1}\) |
因为 \([i,nxt_i-1]\) 区间内的字符都一样,所以我们比较的就是 \(str_{nxt_i-1}\) 与 \(str_{nxt_i}\)。由于 \(str_i=str_{nxt_i-1}\),所以我们最后只需要比较 \(str_i\) 与 \(str_{nxt_i}\) 就可以知道删去了第 \(i\) 个字符的字符串和删去了第 \(nxt_i+q\ (nxt_i+q<len,q\geq 0)\) 个字符的字符串的大小,所以如果 \(str_i<str_{nxt_i}\),我们就可以确定删去了第 \(i\) 个字符的字符串是还未排序的字符串中字典序最小的那一个,所以放在 \(l\) 位置上。反之亦然。证毕。
我们排序的时间便降为了 \(O(L)\)。总时间复杂度为 \(O(L\log L+L)\) 明显可以通过此题。
可是我被卡常了
这种其实卡常没意思,思路才是最关键的,我就放一个被卡常的代码吧。可以通过Easier Version的所有测试点
//Don't act like a loser.
//You can only use the code for studying or finding mistakes
//Or,you'll be punished by Sakyamuni!!!
#include<bits/stdc++.h>
using namespace std;
const int P[2]={33,37},MOD[2]={20060527,21071179},MAXN=1e5+10,ANSMOD=1e9+7;
long long f[2][MAXN*10],p[2][MAXN*10],tmp[MAXN*10];
long long sum[2][MAXN*10]={};
int n=0,nxt[MAXN*10]={};
vector<pair<int,int> > myhsh[MAXN];
string str[MAXN];
inline void myhsh_generator(int x) {
int ret[2]={};
int sz=str[x].size();
for(int i=0;i<sz;i++) {
for(int j=0;j<=1;j++) {
ret[j]=(ret[j]*P[j]%MOD[j]+(int)str[x][i])%MOD[j];
}
myhsh[x].push_back(make_pair(ret[0],ret[1]));
}
}
inline pair<int,int> consecutive_myhsh_query(int x,int l,int r) {
if(l>r) {
return make_pair(0,0);
}
pair<int,int> ret=make_pair(myhsh[x][r].first,myhsh[x][r].second);
if(l!=0) {
ret.first=(ret.first-p[0][r-l+1]*myhsh[x][l-1].first%MOD[0]+MOD[0])%MOD[0];
ret.second=(ret.second-p[1][r-l+1]*myhsh[x][l-1].second%MOD[1]+MOD[1])%MOD[1];
}
return ret;
}
inline pair<int,int> myhsh_query(int x,int l,int r,int del) {
int sz=str[x].size();
if(del<=l) {
l++;
}
if(del<=r) {
r++;
}
l=min(sz-1,l);
r=min(sz-1,r);
if(l<=del&&del<=r) {
pair<int,int> left=consecutive_myhsh_query(x,l,del-1);
pair<int,int> right=consecutive_myhsh_query(x,del+1,r);
pair<int,int> ret=make_pair(0,0);
ret.first=(left.first*p[0][max(r-del,0)]%MOD[0]+right.first)%MOD[0];
ret.second=(left.second*p[1][max(r-del,0)]%MOD[1]+right.second)%MOD[1];
return ret;
}
return consecutive_myhsh_query(x,l,r);
}
inline bool compare(int x,int delx,int y,int dely) {
int len1=str[x].size();
int len2=str[y].size();
if(delx!=len1-1) len1--;
if(dely!=len2-1) len2--;
int l=0,r=min(len1,len2)-2;
while(l<r) {
int mid=(l+r)>>1;
if(myhsh_query(x,l,mid,delx)==myhsh_query(y,l,mid,dely)) {
l=mid+1;
}
else {
r=mid;
}
}
if(myhsh_query(x,l,l,delx)!=myhsh_query(y,l,l,dely)) {
return myhsh_query(x,l,l,delx)<=myhsh_query(y,l,l,dely);
}
return len1<=len2;
}
struct strpair {
int del,id;
bool operator <=(const strpair& a)const {
return compare(id,del,a.id,a.del);
}
};
strpair make_strpair(int x,int y) {
strpair ret;
ret.del=x;
ret.id=y;
return ret;
}
vector<strpair> s[MAXN];
inline void get_next(int x) {
int sz=str[x].size();
fill(nxt,nxt+sz,0);
for(int i=sz-1;i>=0;i--) {
if(str[x][i]!=str[x][i+1]) {
nxt[i]=i+1;
}
else {
nxt[i]=nxt[i+1];
}
}
}
char ch[MAXN*10];
signed main() {
cin>>n;
p[0][0]=1;p[1][0]=1;
for(int i=1;i<=1000000;i++) {
p[0][i]=p[0][i-1]*P[0]%MOD[0];
p[1][i]=p[1][i-1]*P[1]%MOD[1];
}
gets(ch);
for(int i=1;i<=n;i++) {
gets(ch);
str[i]=ch;
str[i]=str[i]+'#';
myhsh_generator(i);
get_next(i);
int sz=str[i].size();
int l=1,r=sz;
for(int j=0;j<sz;j++) {
if(str[i][j]<str[i][nxt[j]]) {
tmp[r--]=j;
}
else {
tmp[l++]=j;
}
}
for(int j=1;j<=sz;j++) {
s[i].push_back(make_strpair(tmp[j],i));
}
/*printf("\n");
for(vector<strpair>::iterator j=s[i].begin();j!=s[i].end();j++) {
for(int k=0;k<sz;k++) {
if(k!=(*j).del) {
cout<<str[i][k];
}
}
printf("\n");
}
printf("\n");*/
}
for(int i=1;i<=n;i++) {
int sz=str[i].size();
int szlast=str[i-1].size();
int k=-1;
for(int t=0;t<sz;t++) {
if(i==1) {
f[i][t]=1;
continue;
}
while(k<szlast-1&&make_strpair(s[i-1][k+1].del,i-1)<=make_strpair(s[i][t].del,i)) {
k++;
}
if(k>=0) {
f[i%2][t]=sum[(i-1)%2][k];
}
else {
f[i%2][t]=0;
}
}
for(int t=0;t<sz;t++) {
sum[i%2][t]=((t==0? 0:sum[i%2][t-1])+f[i%2][t])%ANSMOD;
}
}
cout<<sum[n%2][s[n].size()-1]<<endl;
return 0;
}


