从一道题谈人工智能哲学
左岸的人,猫,鸡,米要过河,但是猫吃鸡,鸡吃米,所以猫鸡同侧时人必须也同侧,鸡米同侧时人必须同侧。同时人划船可以选择送一件物品或者什么都不送。求所有的过河方案?
解题关键就影藏在题目的表述中,简单来说就是排除一些非法状态,并找出状态之间的转换规律。对于计算机来说要处理这个问题,首先要转化为数学问题。很显然状态可以处理成四元组(a,b,c,d),分别代表人,猫,鸡,米。0代表在左岸,1代表在右岸,那么初态和终态可以表示成(0,0,0,0)和(1,1,1,1)。
首先要从全部穷举的状态中剔除非法状态,保留合法状态。那么四位2进制,一共有16种状态:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
从题目中我们可以获取非法状态具有的特征:猫鸡同侧时人必须也同侧,鸡米同侧时人必须同侧。翻译成数学的语言就是:b=c 且 a=~b(非法状态一)或 d=c 且 a=~d(非法状态二),进而可以采用编程的方法剔除,于是就得到了所有的合法状态:
0000
1110
1101
1011
1010
0001
0010
0100
0101
1111
下面我们要考虑状态转换之间的规律,这只需要做一些简单的推理。人在两岸间往返,那么相互转换的状态的a值一定是相反的,这是规律一;另一方面,人每次划船可以带一件或不带东西,那么相互转换的状态的bcd值只能有一位反转或者都没有反转,这是规律二。这两个规律虽然有些抽象但可定时可以用算法描述的。然后我们就得到了下面的状态转换地图:
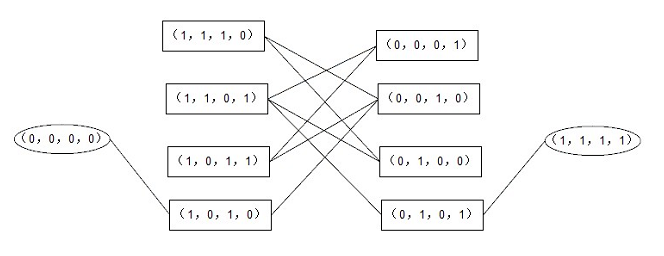
现在我们的问题转化成了寻找状态转换网络中初态到终态的具体路径,这显然是so easy的:
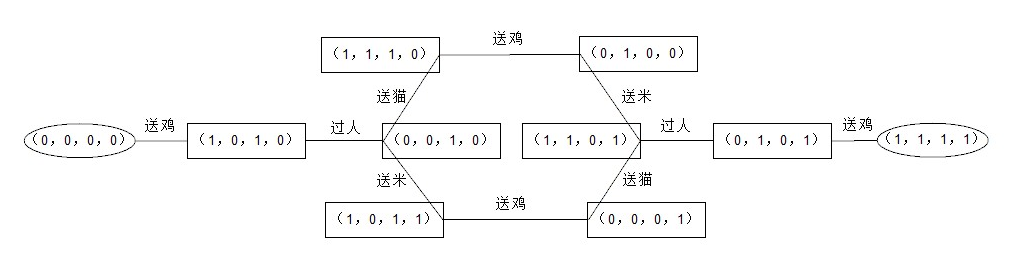
这是人工智能考试的最后一道题,由于时间原因,笔者并没有将其完全解出来,但只是匆匆浏览一下,思路就了然于胸,究其本质不过是道数学题。初一看,要让计算机解决一个如此抽象的问题,确实是需要些智能,但是计算机充其量也不过是台数学机器,又何以能“解决”一个问题。关键点在于如何把现实世界中的问题转化为计算机可处理的数学问题,这才是最核心的部分,而这个过程往往是由人来代替的,所以所有“智能”的背后都是“人工”,机器之所以看起来具有智能是因为人的智能早已凝结在算法中了。从这个角度去看,人工智能更像是智能的传递,从人到机器。在这个过程中最令人着迷的是输出的智能有没有可能大于或等于输入的智能,换句话说机器的智能可能超越人类吗?也许真的存在这种研究智能传递规律的智能论,那么它一定是难以研究的,原因在于智能的不可描述性,像历史上的信息论等学科都是把研究对象描述成数学。而智能目前还是一个抽象的概念,没有任何一个数学公式能描述智能,如果我们接受试着从传递这个角度去看智能,兴许会有新的感悟。





