深入解析LLaMA如何改进Transformer的底层结构
本文分享自华为云社区《大语言模型底层架构你了解多少?LLM大底层架构之LLM模型结构介绍》,作者: 码上开花_Lancer 。
大语言模型结构当前绝大多数大语言模型结构都采用了类似GPT 架构,使用基于Transformer 架构构造的仅由解码器组成的网络结构,采用自回归的方式构建语言模型。但是在位置编码、层归一化位置以及激活函数等细节上各有不同。上篇文章 介绍了GPT-3 模型的训练过程,包括模型架构、训练数据组成、训练过程以及评估方法。
由于GPT-3 并没有开放源代码,根据论文直接重现整个训练过程并不容易,因此根据GPT-3 的描述复现的过程,并构造开源了系统OPT(OpenPre-trained Transformer Language Models)。Meta AI 也仿照GPT-3 架构开源了LLaMA 模型,公开评测结果以及利用该模型进行有监督微调后的模型都有非常好的表现。由于自GPT-3 模型之后,OpenAI 就不再开源也没有开源模型,因此并不清楚ChatGPT 和GPT-4 所采用的模型架构。
本篇文章将以LLaMA 模型为例,介绍大语言模型架构在Transformer 原始结构上的改进,并介绍Transformer 模型结构中空间和时间占比最大的注意力机制优化方法。
一、 LLaMA 的模型结构
上篇文章有介绍了LLaMA 所采用的Transformer 结构和细节,与在本篇文章所介绍的Transformer架构不同的地方包括采用了前置层归一化(Pre-normalization)并使用RMSNorm 归一化函数(Normalizing Function)、激活函数更换为SwiGLU,并使用了旋转位置嵌入(RoP),整体Transformer架构与GPT-2 类似,如图1.1所示。

图1.1 GPT-2 模型结构
接下来,将分别介绍RMSNorm 归一化函数、SwiGLU 激活函数和旋转位置嵌入(RoPE)的具体内容和实现。
1.1. RMSNorm 归一化函数
为了使得模型训练过程更加稳定,GPT-2 相较于GPT 就引入了前置层归一化方法,将第一个层归一化移动到多头自注意力层之前,第二个层归一化也移动到了全连接层之前,同时残差连接的位置也调整到了多头自注意力层与全连接层之后。层归一化中也采用了RMSNorm 归一化函数。针对输入向量aRMSNorm 函数计算公式如下:

此外,RMSNorm 还可以引入可学习的缩放因子gi 和偏移参数bi,从而得到

RMSNorm 在HuggingFace Transformer 库中代码实现如下所示:
class LlamaRMSNorm(nn.Module): def __init__(self, hidden_size, eps=1e-6): """ LlamaRMSNorm is equivalent to T5LayerNorm """ super().__init__() self.weight = nn.Parameter(torch.ones(hidden_size)) self.variance_epsilon = eps # eps 防止取倒数之后分母为0 def forward(self, hidden_states): input_dtype = hidden_states.dtype variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True) hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon) # weight 是末尾乘的可训练参数, 即g_i return (self.weight * hidden_states).to(input_dtype)
1.2. SwiGLU 激活函数
SwiGLU[50] 激活函数是Shazeer 在文献中提出,并在PaLM等模中进行了广泛应用,并且取得了不错的效果,相较于ReLU 函数在大部分评测中都有不少提升。在LLaMA 中全连接层使用带有SwiGLU 激活函数的FFN(Position-wise Feed-Forward Network)的计算公式如下:

其中,σ(x) 是Sigmoid 函数。图1.2给出了Swish 激活函数在参数β 不同取值下的形状。可以看到当β 趋近于0 时,Swish 函数趋近于线性函数y = x,当β 趋近于无穷大时,Swish 函数趋近于ReLU 函数,β 取值为1 时,Swish 函数是光滑且非单调。在HuggingFace 的Transformer 库中Swish1 函数使用silu 函数 代替。
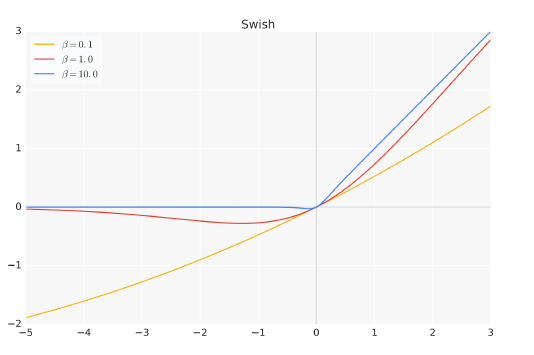
图1.2 Swish 激活函数在参数β 不同取值下的形状
1.3. 旋转位置嵌入(RoPE)
在位置编码上,使用旋转位置嵌入(Rotary Positional Embeddings,RoPE)[52] 代替原有的绝对位置编码。RoPE 借助了复数的思想,出发点是通过绝对位置编码的方式实现相对位置编码。其目标是通过下述运算来给q,k 添加绝对位置信息:

经过上述操作后, ˜qm 和˜kn 就带有位置m 和n 的绝对位置信息。
最终可以得到二维情况下用复数表示的RoPE:

根据复数乘法的几何意义,上述变换实际上是对应向量旋转,所以位置向量称为“旋转式位置编码”。还可以使用矩阵形式表示:

根据内积满足线性叠加的性质,任意偶数维的RoPE,都可以表示为二维情形的拼接,即:

由于上述矩阵Rn 具有稀疏性,因此可以使用逐位相乘⊗ 操作进一步加快计算速度。RoPE 在HuggingFace Transformer 库中代码实现如下所示:
class LlamaRotaryEmbedding(torch.nn.Module): def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None): super().__init__() inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim)) self.register_buffer("inv_freq", inv_freq) # Build here to make `torch.jit.trace` work. self.max_seq_len_cached = max_position_embeddings t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device, dtype=self.inv_freq.dtype) freqs = torch.einsum("i,j->ij", t, self.inv_freq) # Different from paper, but it uses a different permutation # in order to obtain the same calculation emb = torch.cat((freqs, freqs), dim=-1) dtype = torch.get_default_dtype() self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(dtype), persistent=False) self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(dtype), persistent=False) def forward(self, x, seq_len=None): # x: [bs, num_attention_heads, seq_len, head_size] # This `if` block is unlikely to be run after we build sin/cos in `__init__`. # Keep the logic here just in case. if seq_len > self.max_seq_len_cached: self.max_seq_len_cached = seq_len t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype) freqs = torch.einsum("i,j->ij", t, self.inv_freq) # Different from paper, but it uses a different permutation # in order to obtain the same calculation emb = torch.cat((freqs, freqs), dim=-1).to(x.device) self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(x.dtype), persistent=False) self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(x.dtype), persistent=False) return ( self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype), self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype), ) def rotate_half(x): """Rotates half the hidden dims of the input.""" x1 = x[..., : x.shape[-1] // 2] x2 = x[..., x.shape[-1] // 2 :] return torch.cat((-x2, x1), dim=-1) def apply_rotary_pos_emb(q, k, cos, sin, position_ids): # The first two dimensions of cos and sin are always 1, so we can `squeeze` them. cos = cos.squeeze(1).squeeze(0) # [seq_len, dim] sin = sin.squeeze(1).squeeze(0) # [seq_len, dim] cos = cos[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim] sin = sin[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim] q_embed = (q * cos) + (rotate_half(q) * sin) k_embed = (k * cos) + (rotate_half(k) * sin) return q_embed, k_embed
1.4. 模型整体框架
基于上述模型和网络结构可以实现解码器层,根据自回归方式利用训练语料进行模型的过程与本文介绍的过程基本一致。不同规模LLaMA 模型所使用的具体超参数如表1.3所示。但是由于大语言模型的参数量非常大,并且需要大量的数据进行训练,因此仅利用单个GPU 很难完成训练,需要依赖分布式模型训练框架(后面文章将详细介绍相关内容)。
表1.3 LLaMA 不同模型规模下的具体超参数细节

HuggingFace Transformer 库中LLaMA 解码器整体实现代码实现如下所示:
class LlamaDecoderLayer(nn.Module): def __init__(self, config: LlamaConfig): super().__init__() self.hidden_size = config.hidden_size self.self_attn = LlamaAttention(config=config) self.mlp = LlamaMLP( hidden_size=self.hidden_size, intermediate_size=config.intermediate_size, hidden_act=config.hidden_act, ) self.input_layernorm = LlamaRMSNorm(config.hidden_size, eps=config.rms_norm_eps) self.post_attention_layernorm = LlamaRMSNorm(config.hidden_size, eps=config.rms_norm_eps) def forward( self, hidden_states: torch.Tensor, attention_mask: Optional[torch.Tensor] = None, position_ids: Optional[torch.LongTensor] = None, past_key_value: Optional[Tuple[torch.Tensor]] = None, output_attentions: Optional[bool] = False, use_cache: Optional[bool] = False, ) -> Tuple[torch.FloatTensor, Optional[Tuple[torch.FloatTensor, torch.FloatTensor]]]: residual = hidden_states hidden_states = self.input_layernorm(hidden_states) # Self Attention hidden_states, self_attn_weights, present_key_value = self.self_attn( hidden_states=hidden_states, attention_mask=attention_mask, position_ids=position_ids, past_key_value=past_key_value, output_attentions=output_attentions, use_cache=use_cache, ) hidden_states = residual + hidden_states # Fully Connected residual = hidden_states hidden_states = self.post_attention_layernorm(hidden_states) hidden_states = self.mlp(hidden_states) hidden_states = residual + hidden_states outputs = (hidden_states,) if output_attentions: outputs += (self_attn_weights,) if use_cache: outputs += (present_key_value,) return outputs
二、注意力机制优化
在Transformer 结构中,自注意力机制的时间和存储复杂度与序列的长度呈平方的关系,因此占用了大量的计算设备内存和并消耗大量计算资源。因此,如何优化自注意力机制的时空复杂度、增强计算效率是大语言模型需要面临的重要问题。一些研究从近似注意力出发,旨在减少注意力计算和内存需求,提出了包括稀疏近似、低秩近似等方法。此外,也有一些研究从计算加速设备本身的特性出发,研究如何更好利用硬件特性对Transformer 中注意力层进行高效计算。本文将分别介绍上述两类方法。
2.1. 稀疏注意力机制
通过对一些训练好的Transformer 模型中的注意力矩阵进行分析发现,其中很多通常是稀疏的,因此可以通过限制Query-Key 对的数量来减少计算复杂度。这类方法就称为稀疏注意力(SparseAttention)机制。可以将稀疏化方法进一步分成两类:基于位置信息和基于内容。基于位置的稀疏注意力机制的基本类型如图2.6所示,主要包含如下五种类型:
(1)全局注意力(Global Attention):为了增强模型建模长距离依赖关系,可以加入一些全局节点;
(2)带状注意力(Band Attention):大部分数据都带有局部性,限制Query 只与相邻的几个节点进行交互;
(3)膨胀注意力(Dilated Attention);与CNN 中的Dilated Conv 类似,通过增加空隙以获取更大的感受野;
(4)随机注意力(Random Attention):通过随机采样,提升非局部的交互;
(5)局部块注意力(Block Local Attention):使用多个不重叠的块(Block)来限制信息交互。

图2.1 五种基于位置的稀疏注意力基本类型
现有的稀疏注意力机制,通常是基于上述五种基本基于位置的稀疏注意力机制的复合模式,图2.2给出了一些典型的稀疏注意力模型。
Star-Transformer[54] 使用带状注意力和全局注意力的组合。具体来说,Star-Transformer 只包括一个全局注意力节点和宽度为3 的带状注意力,其中任意两个非相邻节点通过一个共享的全局注意力连接,而相邻节点则直接相连。
Longformer使用带状注意力和内部全局节点注意力(Internal Global-node Attention)的组合。此外,Longformer 还将上层中的一些带状注意力头部替换为具有扩张窗口的注意力,在增加感受野同时并不增加计算量。Extended Transformer Construction(ETC)利用带状注意力和外部全局节点注意力(External Global-node Attention)的组合。ETC 稀疏注意力还包括一种掩码机制来处理结构化输入,并采用对比预测编码(Contrastive Predictive Coding,CPC)进行预训练。
BigBird使用带状和全局注意力,还使用额外的随机注意力来近似全连接注意力,此外还揭示了稀疏编码器和稀疏解码器的使用可以模拟任何图灵机,这也在一定程度上解释了,为什么稀疏注意力模型可以取得较好的结果原因。

图2.2 基于位置复合稀疏注意力类型
基于内容的稀疏注意力是是根据输入数据来创建稀疏注意力,其中一种很简单的方法是选择和给定查询(Query)有很高相似度的键(Key)。Routing Transformer 采用K-means 聚类方法,针对 和
和 一起进行聚类,类中心向量集合为
一起进行聚类,类中心向量集合为 ,其中k 是类中心个数。每个Query 只与其处在相同簇(Cluster)下的Key 进行交互。中心向量采用滑动平均的方法进行更新:
,其中k 是类中心个数。每个Query 只与其处在相同簇(Cluster)下的Key 进行交互。中心向量采用滑动平均的方法进行更新:

其中|μ| 表示在簇μ 中向量的数量。Reformer[60] 则采用局部敏感哈希(Local-Sensitive Hashing,LSH)方法来为每个Query 选择Key-Value 对。其主要思想使用LSH 函数将Query 和Key 进行哈希计算,将它们划分到多个桶内。提升在同一个桶内的Query 和Key 参与交互的概率。假设b 是桶的个数,给定一个大小为[Dk, b/2]随机矩阵R,LSH 函数定义为:

如果hqi = hkj 时,qi 才可以与相应的Key-Value 对进行交互。
2.2. FlashAttention
NVIDIA GPU 中的内存(显存)按照它们物理上是在GPU 芯片内部还是板卡RAM 存储芯片上,决定了它们的速度、大小以及访问限制。GPU 显存分为全局内存(Global memory)、本地内存(Local memory)、共享内存(Shared memory,SRAM)、寄存器内存(Register memory)、常量内存(Constant memory)、纹理内存(Texture memory)等六大类。图2.8给出了NVIDIA GPU 内存的整体结构。其中全局内存、本地内存、共享内存和寄存器内存具有读写能力。
全局内存和本地内存使用的高带宽显存(High Bandwidth Memory,HBM)位于板卡RAM 存储芯片上,该部分内存容量很大。全局内存是所有线程都可以访问,而本地内存则只能当前线程访问。NVIDIA H100 中全局内存有80GB 空间,其访问速度虽然可以达到3.35TB/s,但是如果全部线程同时访问全局内存时,其平均带宽仍然很低。共享内存和寄存器位于GPU 芯片上,因此容量很小,并且共享内存只有在同一个GPU 线程块(Thread Block)内的线程才可以共享访问,而寄存器仅限于同一个线程内部才能访问。
NVIDIA H100 中每个GPU 线程块在流式多处理器(Stream Multi-processor,SM)可以使用的共享存储容量仅有228KB,但是其速度非常快,远高于全局内存的访问速度。

图2.2 NVIDIA GPU 的整体内存结构图
在本章第2.2 节中介绍自注意力机制的原理,在GPU 中进行计算时,传统的方法还需要引入:两个中间矩阵S 和P 并存储到全局内存中。具体计算过程如下:

按照上述计算过程,需要首先从全局内存中读取矩阵Q 和K,并将计算好的矩阵S 再写入全局内存,之后再从全局内存中获取矩阵S,计算Softmax 得到矩阵P,再写入全局内容,之后读取矩
阵P 和矩阵V ,计算得到矩阵矩阵O。这样的过程会极大占用显存的带宽。在自注意力机制中,计算速度比内存速度快得多,因此计算效率越来越多地受到全局内存访问的瓶颈。
FlashAttention就是通过利用GPU 硬件中的特殊设计,针对全局内存和共享存储的I/O 速度的不同,尽可能的避免HBM 中读取或写入注意力矩阵。
FlashAttention 目标是尽可能高效地使用SRAM 来加快计算速度,避免从全局内存中读取和写入注意力矩阵。达成该目标需要能做到在不访问整个输入的情况下计算Softmax 函数,并且后向传播中不能存储中间注意力矩阵。
标准Attention 算法中,Softmax 计算按行进行,即在与V 做矩阵乘法之前,需要将Q、K 的各个分块完成一整行的计算。在得到Softmax 的结果后,再与矩阵V 分块做矩阵乘。而在FlashAttention 中,将输入分割成块,并在输入块上进行多次传递,从而以增量方式执行Softmax 计算。
自注意力算法的标准实现将计算过程中的矩阵S、P 写入全局内存中,而这些中间矩阵的大小与输入的序列长度有关且为二次型。因此,FlashAttention 就提出了不使用中间注意力矩阵,通过存储归一化因子来减少全局内存的消耗。
FlashAttention 算法并没有将S、P 整体写入全局内存,而是通过分块写入,存储前向传递的Softmax 归一化因子,在后向传播中快速重新计算片上注意力,这比从全局内容中读取中间注意力矩阵的标准方法更快。由于大幅度减少了全局内存的访问量,即使重新计算导致FLOPs 增加,但其运行速度更快并且使用更少的内存。具体算法如代码2.2所示,其中内循环和外循环所对应的计算可以参考下图。

2.3 FlashAttention 计算流程图
2.3. 多查询注意力
多查询注意力(Multi Query Attention)[62] 是多头注意力的一种变体。其主要区别在于,在多查询注意力中不同的注意力头共享一个键和值的集合,每个头只单独保留了一份查询参数。
因此键和值的矩阵仅有一份,这大幅度减少了显存占用,使其更高效。由于多查询注意力改变了注意力机制的结构,因此模型通常需要从训练开始就支持多查询注意力。文献[63] 的研究结果表明,可以通过对已经训练好的模型进行微调来添加多查询注意力支持,仅需要约5% 的原始训练数据量就可以达到不错的效果。包括Falcon、SantaCoder、StarCoder等在内很多模型都采用了多查询注意力机制。
以LLM Foundry 为例,多查询注意力实现代码如下:
代码2.2: FlashAttention 算法,简单来说我梳理下逻辑:

class MultiQueryAttention(nn.Module): """Multi-Query self attention. Using torch or triton attention implemetation enables user to also use additive bias. """ def __init__( self, d_model: int, n_heads: int, device: Optional[str] = None, ): super().__init__() self.d_model = d_model self.n_heads = n_heads self.head_dim = d_model // n_heads self.Wqkv = nn.Linear( # Multi-Query Attention 创建 d_model, d_model + 2 * self.head_dim, # 只创建查询的头向量,所以只有1 个d_model device=device, # 而键和值则共享各自的一个head_dim 的向量 ) self.attn_fn = scaled_multihead_dot_product_attention self.out_proj = nn.Linear( self.d_model, self.d_model, device=device ) self.out_proj._is_residual = True # type: ignore def forward( self, x, ): qkv = self.Wqkv(x) # (1, 512, 960) query, key, value = qkv.split( # query -> (1, 512, 768) [self.d_model, self.head_dim, self.head_dim], # key -> (1, 512, 96) dim=2 # value -> (1, 512, 96) ) context, attn_weights, past_key_value = self.attn_fn( query, key, value, self.n_heads, multiquery=True, ) return self.out_proj(context), attn_weights, past_key_value
与LLM Foundry 中实现的多头自注意力代码相对比,其区别仅在于建立Wqkv 层上:
# Multi Head Attention self.Wqkv = nn.Linear( # Multi-Head Attention 的创建方法 self.d_model, 3 * self.d_model, # 查询、键和值3 个矩阵, 所以是3 * d_model device=device ) query, key, value = qkv.chunk( # 每个tensor 都是(1, 512, 768) 3, dim=2 ) # Multi Query Attention self.Wqkv = nn.Linear( # Multi-Query Attention 的创建方法 d_model, d_model + 2 * self.head_dim, # 只创建查询的头向量,所以是1* d_model device=device, # 而键和值不再具备单独的头向量 ) query, key, value = qkv.split( # query -> (1, 512, 768) [self.d_model, self.head_dim, self.head_dim], # key -> (1, 512, 96) dim=2 # value -> (1, 512, 96) )
本篇文章将以LLaMA 模型为例,从底层详细的介绍了大语言模型架构在Transformer 原始结构上的改进,并介绍Transformer 模型结构中空间和时间占比最大的注意力机制优化方法。看起来确实比较“干”货一点,但是只有从底层更加了解大模型原理,才能更加知道怎么使用。



