AUC/ROC:面试中80%都会问的知识点
摘要:ROC/AUC作为机器学习的评估指标非常重要,也是面试中经常出现的问题(80%都会问到)
本文分享自华为云社区《技术干货 | 解决面试中80%问题,基于MindSpore实现AUC/ROC》,原文作者:李嘉琪。
ROC/AUC作为机器学习的评估指标非常重要,也是面试中经常出现的问题(80%都会问到)。其实,理解它并不是非常难,但是好多朋友都遇到了一个相同的问题,那就是:每次看书的时候都很明白,但回过头就忘了,经常容易将概念弄混。还有的朋友面试之前背下来了,但是一紧张大脑一片空白全忘了,导致回答的很差。
我在之前的面试过程中也遇到过类似的问题,我的面试经验是:一般笔试题遇到选择题基本都会考这个率,那个率,或者给一个场景让你选用哪个。面试过程中也被问过很多次,比如什么是AUC/ROC?横轴纵轴都代表什么?有什么优点?为什么要使用它?
我记得在我第一次回答的时候,我将准确率,精准率,召回率等概念混淆了,最后一团乱。回去以后我从头到尾梳理了一遍所有相关概念,后面的面试基本都回答地很好。现在想将自己的一些理解分享给大家,希望读完本篇可以彻底记住ROC/AUC的概念。

ROC的全名叫做Receiver Operating Characteristic,其主要分析工具是一个画在二维平面上的曲线——ROC 曲线。平面的横坐标是false positive rate(FPR),纵坐标是true positive rate(TPR)。对某个分类器而言,我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样,此分类器就可以映射成ROC平面上的一个点。调整这个分类器分类时候使用的阈值,我们就可以得到一个经过(0, 0),(1, 1)的曲线,这就是此分类器的ROC曲线。一般情况下,这个曲线都应该处于(0, 0)和(1, 1)连线的上方。因为(0, 0)和(1, 1)连线形成的ROC曲线实际上代表的是一个随机分类器。如果很不幸,你得到一个位于此直线下方的分类器的话,一个直观的补救办法就是把所有的预测结果反向,即:分类器输出结果为正类,则最终分类的结果为负类,反之,则为正类。虽然,用ROC 曲线来表示分类器的性能很直观好用。
可是,人们总是希望能有一个数值来标志分类器的好坏。于是Area Under roc Curve(AUC)就出现了。顾名思义,AUC的值就是处于ROC 曲线下方的那部分面积的大小。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的性能。AUC(Area Under roc Curve)是一种用来度量分类模型好坏的一个标准。
ROC示例曲线(二分类问题):
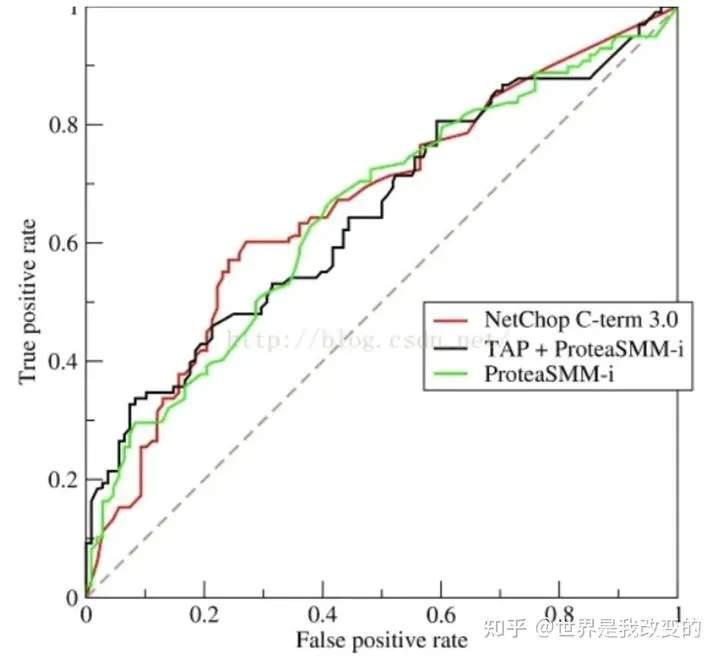
解读ROC图的一些概念定义:
- 真正(True Positive , TP)被模型预测为正的正样本;
- 假负(False Negative , FN)被模型预测为负的正样本;
- 假正(False Positive , FP)被模型预测为正的负样本;
- 真负(True Negative , TN)被模型预测为负的负样本。
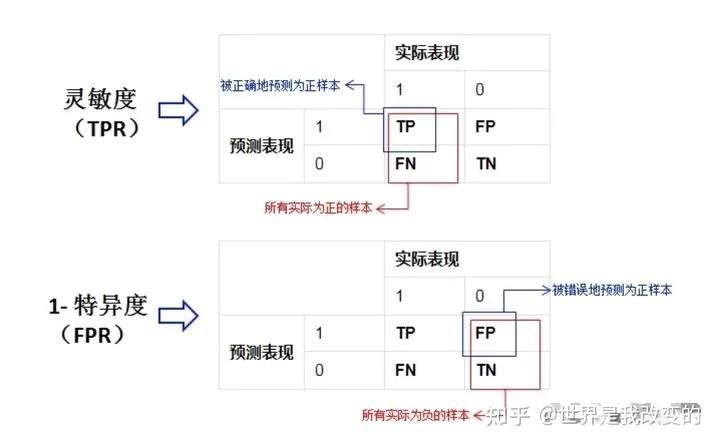
灵敏度,特异度,真正率,假正率
在正式介绍ROC/AUC之前,我们需要介绍两个指标,这两个指标的选择也正是ROC和AUC可以无视样本不平衡的原因。这两个指标分别是:灵敏度和(1-特异度),也叫做真正率(TPR)和假正率(FPR)。
灵敏度(Sensitivity) = TP/(TP+FN)
特异度(Specificity) = TN/(FP+TN)
其实我们可以发现灵敏度和召回率是一模一样的,只是名字换了而已。
由于我们比较关心正样本,所以需要查看有多少负样本被错误地预测为正样本,所以使用(1-特异度),而不是特异度。
真正率(TPR) = 灵敏度 = TP/(TP+FN)
假正率(FPR) = 1- 特异度 = FP/(FP+TN)
下面是真正率和假正率的示意,我们发现TPR和FPR分别是基于实际表现1和0出发的,也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。
正因为如此,所以无论样本是否平衡,都不会被影响。比如总样本中,90%是正样本,10%是负样本。我们知道用准确率是有水分的,但是用TPR和FPR不一样。这里,TPR只关注90%正样本中有多少是被真正覆盖的,而与那10%毫无关系,同理,FPR只关注10%负样本中有多少是被错误覆盖的,也与那90%毫无关系,所以可以看出:
如果我们从实际表现的各个结果角度出发,就可以避免样本不平衡的问题了,这也是为什么选用TPR和FPR作为ROC/AUC的指标的原因。
或者我们也可以从另一个角度考虑:条件概率。我们假设X为预测值,Y为真实值。那么就可以将这些指标按条件概率表示:
- 精准率 = P(Y=1 | X=1)
- 召回率 = 灵敏度 = P(X=1 | Y=1)
- 特异度 = P(X=0 | Y=0)
从上面三个公式看到:如果我们先以实际结果为条件(召回率,特异度),那么就只需考虑一种样本,而先以预测值为条件(精准率),那么我们需要同时考虑正样本和负样本。所以先以实际结果为条件的指标都不受样本不平衡的影响,相反以预测结果为条件的就会受到影响。
ROC(接受者操作特征曲线)
ROC(Receiver Operating Characteristic)曲线,又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域,用于区分信号与噪声。后来人们将其用于评价模型的预测能力,ROC曲线是基于混淆矩阵得出的。
ROC曲线中的主要两个指标就是真正率和假正率,上面也解释了这么选择的好处所在。其中横坐标为假正率(FPR),纵坐标为真正率(TPR),下面就是一个标准的ROC曲线图。
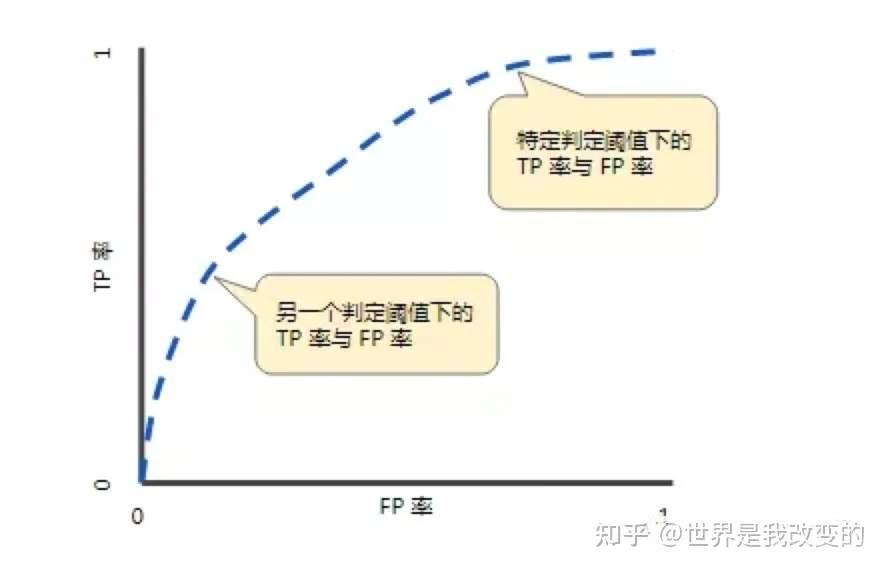
-
ROC曲线的阈值问题
与前面的P-R曲线类似,ROC曲线也是通过遍历所有阈值来绘制整条曲线的。如果我们不断的遍历所有阈值,预测的正样本和负样本是在不断变化的,相应的在ROC曲线图中也会沿着曲线滑动。
-
如何判断ROC曲线的好坏?
改变阈值只是不断地改变预测的正负样本数,即TPR和FPR,但是曲线本身是不会变的。那么如何判断一个模型的ROC曲线是好的呢?这个还是要回归到我们的目的:FPR表示模型虚报的响应程度,而TPR表示模型预测响应的覆盖程度。我们所希望的当然是:虚报的越少越好,覆盖的越多越好。所以总结一下就是TPR越高,同时FPR越低(即ROC曲线越陡),那么模型的性能就越好。参考如下动态图进行理解。
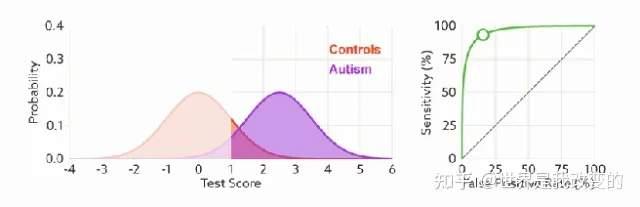
-
ROC曲线无视样本不平衡
前面已经对ROC曲线为什么可以无视样本不平衡做了解释,下面我们用动态图的形式再次展示一下它是如何工作的。我们发现:无论红蓝色样本比例如何改变,ROC曲线都没有影响。
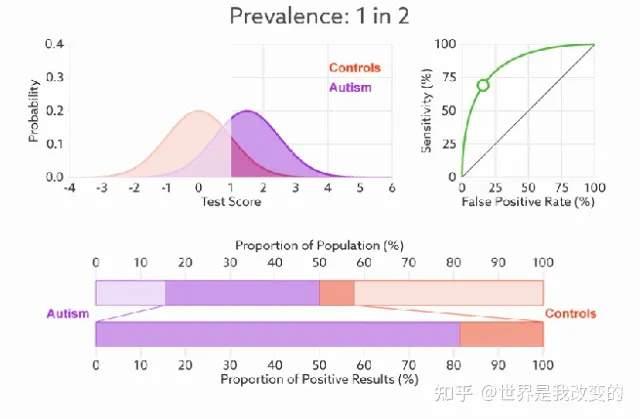
AUC(曲线下的面积)
为了计算 ROC 曲线上的点,我们可以使用不同的分类阈值多次评估逻辑回归模型,但这样做效率非常低。幸运的是,有一种基于排序的高效算法可以为我们提供此类信息,这种算法称为曲线下面积(Area Under Curve)。
比较有意思的是,如果我们连接对角线,它的面积正好是0.5。对角线的实际含义是:随机判断响应与不响应,正负样本覆盖率应该都是50%,表示随机效果。ROC曲线越陡越好,所以理想值就是1,一个正方形,而最差的随机判断都有0.5,所以一般AUC的值是介于0.5到1之间的。
-
AUC的一般判断标准
0.5 - 0.7:效果较低,但用于预测股票已经很不错了0.7 - 0.85:效果一般0.85 - 0.95:效果很好0.95 - 1:效果非常好,但一般不太可能
-
AUC的物理意义
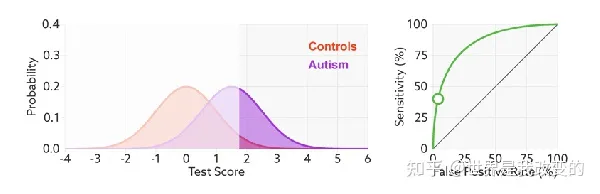
曲线下面积对所有可能的分类阈值的效果进行综合衡量。曲线下面积的一种解读方式是看作模型将某个随机正类别样本排列在某个随机负类别样本之上的概率。以下面的样本为例,逻辑回归预测从左到右以升序排列:


好了,原理已经讲完,上MindSpore框架的代码。
MindSpore代码实现(ROC)
"""ROC""" import numpy as np from mindspore._checkparam import Validator as validator from .metric import Metric class ROC(Metric): def __init__(self, class_num=None, pos_label=None): super().__init__() # 分类数为一个整数 self.class_num = class_num if class_num is None else validator.check_value_type("class_num", class_num, [int]) # 确定正类的整数,对于二分类问题,它被转换为1。对于多分类问题,不应设置此参数,因为它在[0,num_classes-1]范围内迭代更改。 self.pos_label = pos_label if pos_label is None else validator.check_value_type("pos_label", pos_label, [int]) self.clear() def clear(self): """清除历史数据""" self.y_pred = 0 self.y = 0 self.sample_weights = None self._is_update = False def _precision_recall_curve_update(self, y_pred, y, class_num, pos_label): """更新曲线""" if not (len(y_pred.shape) == len(y.shape) or len(y_pred.shape) == len(y.shape) + 1): raise ValueError("y_pred and y must have the same number of dimensions, or one additional dimension for" " y_pred.") # 二分类验证 if len(y_pred.shape) == len(y.shape): if class_num is not None and class_num != 1: raise ValueError('y_pred and y should have the same shape, but number of classes is different from 1.') class_num = 1 if pos_label is None: pos_label = 1 y_pred = y_pred.flatten() y = y.flatten() # 多分类验证 elif len(y_pred.shape) == len(y.shape) + 1: if pos_label is not None: raise ValueError('Argument `pos_label` should be `None` when running multiclass precision recall ' 'curve, but got {}.'.format(pos_label)) if class_num != y_pred.shape[1]: raise ValueError('Argument `class_num` was set to {}, but detected {} number of classes from ' 'predictions.'.format(class_num, y_pred.shape[1])) y_pred = y_pred.transpose(0, 1).reshape(class_num, -1).transpose(0, 1) y = y.flatten() return y_pred, y, class_num, pos_label def update(self, *inputs): """ 更新预测值和真实值。 """ # 输入数量的校验 if len(inputs) != 2: raise ValueError('ROC need 2 inputs (y_pred, y), but got {}'.format(len(inputs))) # 将输入转为numpy y_pred = self._convert_data(inputs[0]) y = self._convert_data(inputs[1]) # 更新曲线 y_pred, y, class_num, pos_label = self._precision_recall_curve_update(y_pred, y, self.class_num, self.pos_label) self.y_pred = y_pred self.y = y self.class_num = class_num self.pos_label = pos_label self._is_update = True def _roc_(self, y_pred, y, class_num, pos_label, sample_weights=None): if class_num == 1: fps, tps, thresholds = self._binary_clf_curve(y_pred, y, sample_weights=sample_weights, pos_label=pos_label) tps = np.squeeze(np.hstack([np.zeros(1, dtype=tps.dtype), tps])) fps = np.squeeze(np.hstack([np.zeros(1, dtype=fps.dtype), fps])) thresholds = np.hstack([thresholds[0][None] + 1, thresholds]) if fps[-1] <= 0: raise ValueError("No negative samples in y, false positive value should be meaningless.") fpr = fps / fps[-1] if tps[-1] <= 0: raise ValueError("No positive samples in y, true positive value should be meaningless.") tpr = tps / tps[-1] return fpr, tpr, thresholds # 定义三个列表 fpr, tpr, thresholds = [], [], [] for c in range(class_num): preds_c = y_pred[:, c] res = self.roc(preds_c, y, class_num=1, pos_label=c, sample_weights=sample_weights) fpr.append(res[0]) tpr.append(res[1]) thresholds.append(res[2]) return fpr, tpr, thresholds def roc(self, y_pred, y, class_num=None, pos_label=None, sample_weights=None): """roc""" y_pred, y, class_num, pos_label = self._precision_recall_curve_update(y_pred, y, class_num, pos_label) return self._roc_(y_pred, y, class_num, pos_label, sample_weights) def (self): """ 计算ROC曲线。返回的是一个元组,由`fpr`、 `tpr`和 `thresholds`组成的元组。 """ if self._is_update is False: raise RuntimeError('Call the update method before calling .') y_pred = np.squeeze(np.vstack(self.y_pred)) y = np.squeeze(np.vstack(self.y)) return self._roc_(y_pred, y, self.class_num, self.pos_label)
使用方法如下:
- 二分类的例子
import numpy as np from mindspore import Tensor from mindspore.nn.metrics import ROC # binary classification example x = Tensor(np.array([3, 1, 4, 2])) y = Tensor(np.array([0, 1, 2, 3])) metric = ROC(pos_label=2) metric.clear() metric.update(x, y) fpr, tpr, thresholds = metric.() print(fpr, tpr, thresholds) [0., 0., 0.33333333, 0.6666667, 1.] [0., 1, 1., 1., 1.] [5, 4, 3, 2, 1]
- 多分类的例子
import numpy as np from mindspore import Tensor from mindspore.nn.metrics import ROC # multiclass classification example x = Tensor(np.array([[0.28, 0.55, 0.15, 0.05], [0.10, 0.20, 0.05, 0.05], [0.20, 0.05, 0.15, 0.05],0.05, 0.05, 0.05, 0.75]])) y = Tensor(np.array([0, 1, 2, 3])) metric = ROC(class_num=4) metric.clear() metric.update(x, y) fpr, tpr, thresholds = metric.() print(fpr, tpr, thresholds) [array([0., 0., 0.33333333, 0.66666667, 1.]), array([0., 0.33333333, 0.33333333, 1.]), array([0., 0.33333333, 1.]), array([0., 0., 1.])] [array([0., 1., 1., 1., 1.]), array([0., 0., 1., 1.]), array([0., 1., 1.]), array([0., 1., 1.])] [array([1.28, 0.28, 0.2, 0.1, 0.05]), array([1.55, 0.55, 0.2, 0.05]), array([1.15, 0.15, 0.05]), array([1.75, 0.75, 0.05])]
MindSpore代码实现(AUC)
"""auc""" import numpy as np def auc(x, y, reorder=False): """ 使用梯形法则计算曲线下面积(AUC)。这是一个一般函数,给定曲线上的点。计算ROC曲线下的面积。 """ # 输入x是由ROC曲线得到的fpr值或者一个假阳性numpy数组。如果是多类的,这是一个这样的list numpy,每组代表一类。 # 输入y是由ROC曲线得到的tpr值或者一个真阳性numpy数组。如果是多类的,这是一个这样的list numpy,每组代表一类。 if not isinstance(x, np.ndarray) or not isinstance(y, np.ndarray): raise TypeError('The inputs must be np.ndarray, but got {}, {}'.format(type(x), type(y))) # 检查所有数组的第一个维度是否一致。检查数组中的所有对象是否具有相同的形状或长度。 _check_consistent_length(x, y) # 展开列或1d numpy数组。 x = _column_or_1d(x) y = _column_or_1d(y) # 进行校验 if x.shape[0] < 2: raise ValueError('At least 2 points are needed to compute the AUC, but x.shape = {}.'.format(x.shape)) direction = 1 if reorder: order = np.lexsort((y, x)) x, y = x[order], y[order] else: dx = np.diff(x) if np.any(dx < 0): if np.all(dx 1: raise ValueError("Found input variables with inconsistent numbers of samples: {}." .format([int(length) for length in lengths]))
使用方法如下:
- 利用ROC的fpr, tpr值求auc
import numpy as np from mindspore.nn.metrics import auc x = Tensor(np.array([[3, 0, 1], [1, 3, 0], [1, 0, 2]])) y = Tensor(np.array([[0, 2, 1], [1, 2, 1], [0, 0, 1]])) metric = ROC(pos_label=1) metric.clear() metric.update(x, y) fpr, tpr, thre = metric.eval() # 利用ROC的fpr, tpr值求auc output = auc(fpr, tpr) print(output) 0.45


