关于静态分析技术符号执行,从一个故事讲起······
摘要:本文提纲絜领的介绍了符号执行,让大家明白这个技术的主要作用和面临的挑战,领大家入坑。
1. 引言
程序静态分析(Program Static Analysis)是指在不运行代码的方式下,通过词法分析、语法分析、控制流、数据流分析等技术对程序代码进行扫描,验证代码是否满足规范性、安全性、可靠性、可维护性等指标的一种代码分析技术[8]。 程序静态分析的历史几乎与程序的历史一样长, 自从有了程序就有了程序分析。特别是随着编译技术的发展,大大带动了程序的自动分析技术。目前静态分析技术向模拟执行的技术发展以能够发现更多传统意义上动态测试才能发现的缺陷,例如符号执行、抽象解释、值依赖分析等等并采用数学约束求解工具进行路径约减或者可达性分析以发现更多的问题、减少误报、提高效率。
随着程序的规模和复杂度越来越高,现代的程序分析的具体应用中,对一个问题的检查往往不是单一个使用一种技术,而是会同时使用多种分析技术,采用多次迭代,反复求精的过程。 这就要求我们在设计的时候能统一规划,策略对待不同的问题。就好比一个大厨,做每道菜,用什么材料,先放什么,后放什么,用什么火候,放多少都要把控的恰到好处。
这里我打算把这个技术介绍做成一个系列,探讨静态分析中的各种技术,希望通过这些介绍,能够让更多的程序员能够投入到程序分析的行列来,一起进行更深层次的软件自动化方面的探讨和研究。
2. 关于符号执行的一个故事
大家都喜欢听故事,这里先讲一个和符号执行相关的故事作为一个引子。
话说一年一度的网络安全行业盛会RSA大会,每年入选的创新沙盒十强,都会成为业界投资者的追捧,同时从这些项目中,我们也可以推断出网络安全技术创新的热点方向。
今年的十强中有一个叫做Mayhem的产品,对于Mayhem这个名字,搞符号执行的人恐怕并不陌生。
首先这个名字Mayhem让人影响深刻,中文翻译过来就是“混乱”,本来世界就够乱的了,还把工具叫成“混乱”,真是"Complete mayhem"(全乱了)。
把和Mayhem有关的信息,按时间顺序编排一下,就可以看到故事的主线:
· ForAllSecure成立于2012年,其技术源于卡耐基梅隆大学(CMU)研究获得的专利技术;
· 从2012年到2017年,美国国防部(DoD)在几乎所有正在开发的关键武器系统中发现了漏洞。
· 《M国国防法》要求就加强关键系统的软件安全性提出报告,建议在国防高级研究计划局的“网络大挑战”下开发二进制分析和符号执行工具;
· 2016年美国高等研究计划署(DAPRA)主办了自动网络攻防赛(CyberGrandChallenge),旨在建立实时自动化的网络防御系统,并且能够快速地应对大量新的攻击手法,以应对频发的网络攻击。符号执行在参赛队的自动攻防系统中起到了举足轻重的作用,被广泛应用在程序脆弱性的分析上。卡内基梅隆大学ForAllSecure团队的Mayhem获得了CGC的冠军;
· 2018年,GAO-19-128号报告称,由于武器系统的计算机化,武器系统比以往任何时候都更依赖软件,也更加网络化,为了使武器系统防范日益复杂的网络安全攻击,美国国防部(DoD)正在开发更安全的武器系统;
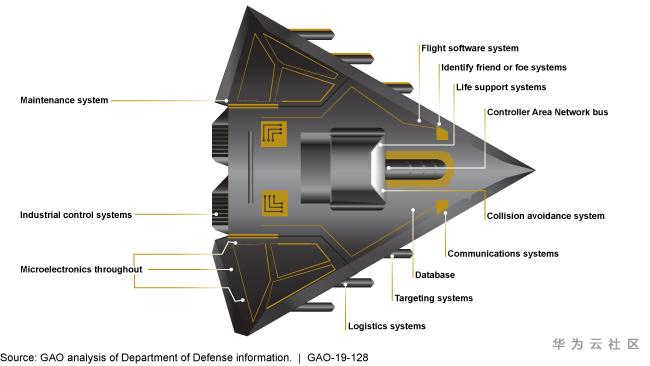
· Mayhem是联邦政府推荐的安全解决方案,用于连续,自动化,准确的测试;
· 美国国防部的多个实体都使用Mayhem,包括但不限于:空军第96网络空间测试小组,空军第90网络空间操作中队,海军海系统司令部(NAVSEA)和美国陆军司令部,控制,通信,计算机,网络,情报,监视和侦察中心(C5ISR)。
Mayhem是ForAllSecure推出的辅助智能行为测试解决方案。它采用符号执行自动生成测试用例,然后通过模糊测试(fuzz)发现软件缺陷。Mayhem将这两种测试技术融合,集成在了DevOps中,持续的发现安全漏洞。
注: 从ForAllSecure的网站(https://forallsecure.com/government-and-defense),可以得到上面的信息。
另:Mayhem[4]使用的是二进制的符号执行框架,属于动态分析的范畴,这里只是作为我们的一个引子,不必要纠结。
接下来,我们提纲絜领的介绍下符号执行,让大家明白这个技术的主要作用和面临的挑战,领大家入坑,更多的细节可以从后面的参考文献中获得。
3. 经典的符号执行技术
符号执行[1]是一种静态分析技术,它可以通过分析技术得到让特定区域执行的输入。最初在1976年由King JC在ACM上提出。即通过使用抽象的符号代替具体值来模拟程序的执行,当遇到分支语句时,它会探索每一个分支, 将分支条件加入到相应的路径约束中,若约束可解,则说明该路径是可达的。符号执行的目的是在给定的时间内,尽可能的探索更多的路径。根据运行的目的来分,主要有两个:
- 从测试的角度来看,它可以模拟出各个路径的输入值,从而创建高覆盖率的测试套件。这里是静态的分析程序得到测试需要的输入,与动态执行程序的测试不同,动态执行程序的测试更多的是依赖完备的测试用例来提升测试的覆盖率,达到发现问题的目的。比如曾经使用过的IBM的Purify 来检测代码的内存泄露问题。就需要人工的看代码,编制大量的测试用例,然后通过让程序执行分别执行这些输入,来提高代码的覆盖率,从而尽可能的发现内存泄漏的问题。
- 从缺陷查找的角度来看,它为开发人员提供了触发的缺陷的具体输入,利用该输入,程序可用于缺陷的确认或调试。符号执行不仅限于查找诸如缓冲区溢出之类的问题,而且可以通过根据缺陷发现的条件,生成复杂的断言,来判断缺陷发生的可能性。
这里举一个经典的例子[2],来说明符号执行的具体过程。
1 int twice(int v){ 2 return 2*v; 3 } 4 5 void testme(int x, int y){ 6 z = twice(y); 7 if (z == x){ 8 if (x > y+10) 9 ERROR; 10 } 11 } 12 13 int main(){ 14 x = sym_input(); 15 y = sym_input(); 16 testme(x, y); 17 return 0; 18 }
这段代码中的函数testme()有三条执行路径。符号执行的目的,就是在给定的时间预算内,生成一组输入,并通过这些输入尽可能多的探索执行路径。
- 执行路径(execution path):一个true和false的序列seq ={p0, p1, …, pn}。其中,如果是一个条件语句,那么pi=ture则表示条件语句的取值为:true,否则取false;
- 执行树(execution tree):一个程序的所有执行路径则可表征成一棵执行树。
下图是样例代码的执行树:
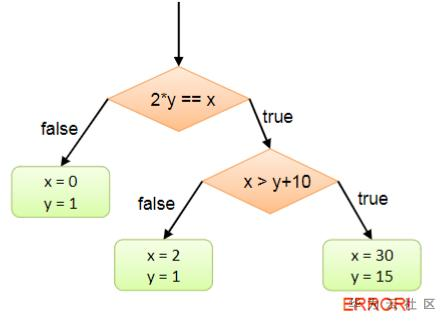
符号执行通过维护符号状态和路径约束,以便在运行过程中传递信息。
- 符号状态(symbolic state):符号执行维护一个符号状态σ,将变量映射到符号表达式。
- 符号路径约束(symbolic path constraint):符号路径约束PC,它是符号表达式上无量词的一阶公式。
- 在执行开始时,将σ初始化为一个空映射,将PC初始化为true;
- 在符号执行过程中,σ和PC都会更新。
- 在沿着程序执行路径的符号执行结束时,使用约束求解器对PC进行求解,以生成具体的输入值。 如果程序在这些具体的输入值上执行,它将采用与符号执行完全相同的路径,并以相同的方式终止。
对于样例代码,具体的过程如下
- 初始化:初始化符号状态σ为空,符号路径约束PC为true;
- 在每个赋值v = e处,符号执行都通过将 v 映射到σ(e)来更新σ,该映射是通过对当前符号状态求值, 而获得的符号表达式。 例如:
- main()函数的前两行(第16-17行)的符号执行导致σ= {x ↦x0,y ↦ y0},其中x0,y0是两个初始不受约束的符号值;
- 在执行第6行之后,σ = {x ↦x0,y ↦y0,z ↦ 2y0}。
- 对于每个条件语句:if(e) then S1 else S2。
- 在第7行之后,分别创建了两个符号执行实例,分别具有路径约束x0 = 2y0和x ≠ 2y0;
- 在第8行之后,分别创建两个具有路径约束的符号执行实例(x0 = 2y0)∧(x0 > y0 + 10)和(x0 = 2y0)∧(x0 ≤ y0 + 10)。
- “then”分支: PC被更新为PC ∧ σ(e);
- “else”分支: 生成一个新的PC', PC'被初始化为:PC∧¬ σ(e);
- 如果分支的状态σ的PC可满足,则符号执行沿着分支继续,否则路径终止。
例如: - 如果一个符号执行实例碰到了exit或error时,当前符号执行实例就会被终止,并利用一个现成的约束求解器来生成一个可满足当前路径约束的赋值。 例如:
- 三条路径按照约束求解后,分别得到我们期望的三组输入:{x=0, y=1},{x=2, y=1}和{x=30, y=15}。
- 若代码中包含循环或递归结构,且它们的终止条件是符号化的,则可能导致有无穷多条路径。在实践过程中,需要对路径搜索设置一个限制,例如timeout,限制路径数量,循环迭代次数或探测深度。
经典的符号执行有一个关键的缺点,若符合执行路径的符号路径约束无法使用约束求解器进行有效的求解,则无法生成输入。
4. 现代符号执行技术
经典的符号执行,过度的依赖了符号执行的约束求解能力,这就限制了传统符号执行的能力发挥。很快大家发现在分析过程中,如果能加入具体值进行分析,将大大简化分析过程,降低分析的难度和提升效率;但分析过程中,仍不可避免的还是需要将各种条件表达式,进行符号化抽象后变成约束条件参与执行。将程序语句转换为符号约束的精度,对符号执行所达到的覆盖率以及约束求解的可伸缩性会产生重大影响。所以如何做好混合具体(Concrete)执行和符号(Symbolic)执行的能力的平衡,就成为现代符号执行的关键点。
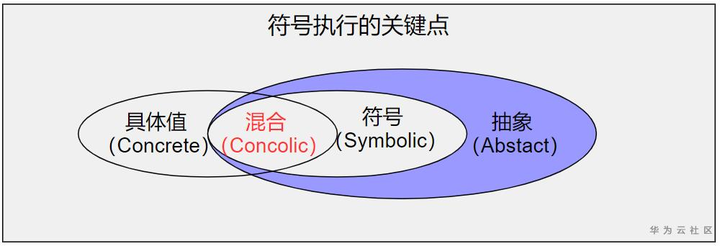
混合执行测试(Concolic testing)[5][6]和执行生成测试(Execution-Generated Testing (EGT))[7]这两种现代符号执行的代表都是基于这个思想发展而来的。下面以混合执行测试(Concolic testing)为例说明下现代符号执行的主要过程。
与经典的符号执行不同,由于混合执行在整个执行过程中,需要维护程序的具体状态,因此其输入需要初始具体值。 混合执行测试从一个给定的输入或随机输入开始执行程序,沿着执行的条件语句在输入上收集符号约束,然后使用约束求解推断先前输入的变化,以便引导程序接下来的执行该走向哪一个执行路径。重复此过程,直到探索了所有执行路径,或者满足用户定义的覆盖标准、时间设置到期为止。
混合执行测试会同时维护两个状态:
· 具体状态:映射所有有具体值的变量;
· 符号状态:仅映射没有具体值的变量。
对于样例代码,执行过程如下:
· 混合执行会生成一些随机的输入值,比如{x=22, y=7},然后符号化和具体化地一起来执行程序。
· 依据{x=22, y=7},程序在第7行,这个具体的执行会走向else分支;符号执行沿着执行路径会生成x ≠ 2y0的路径约束;
· 混合测试将路径约束中的连接(x ≠ 2y0)取反,生成一个新的约束x0=2y0,并求解得到测试输入{x=2, y=1}。这个新的输入会强制让程序执行then路径。
· 依据{x=2, y=1},程序在第8行执行else分支。混合测试会沿着具体执行来进行符号执行,并生成路径约束(x0 = 2y0)∧(x0 > y0 + 10);
· 混合测试将路径约束中的连接((x0 > y0 + 10))取反,会生成一个新约束(x0 = 2y0)∧(x0 ≤ y0 + 10)的测试,求解得到测试输入{x=30, y=15}。在这个输入下程序走到ERROR语句。
· 混合测试报告所有被探索的执行路径,并终止测试输入的生成。
比较混合执行测试和传统的符号执行,不难发现由于具体值的引入,简化了约束求解的难度。
5. 主要挑战和解决方案
符号执行技术已经有了40多年的发展,在2017年8月Google学术中,标题中带有“符号执行”的文章有742篇[3],到2020.11月,文章数上升到1490, 可见符号执行有了飞速的发展。但程序的复杂性和规模也在飞速的发展,符号执行仍然存在路径爆炸(代码规模、复杂度)、约束求解(计算算法)、内存模型(工具设计)等挑战。
5.1. 路径爆炸(Path Explosion)
符号执行在过程处理中默认已经过滤了以下两种路径:
· 不依赖于符号输入的路径;
· 对于当前的路径约束,不可解的路径。 但是,尽管符号执行已经做了这些过滤,路径爆炸依旧是符号执行的最大挑战。路径爆炸不是符号执行特有的挑战,是整个程序分析都需要考虑的最大的问题。
解决路径爆炸的方案,可以从以下两个角度来考虑:
· 减少路径总数(优先的考虑最有希望的路径, 路径合并,剪枝);
· 相似的路径不再分析(函数摘要,缓存);
依据这个思路业界提出了两种解决方案。
· 启发式(Heuristic): 大多数启发式方法侧重于实现较高的语句和分支覆盖率。
1. 特别有效的方法是使用静态控制流图(CFG)来指导探索,向最接近的路径或优先选择先前执行次数最少的语句;
2. 在每个可行的符号分支,随机选择要探索的一侧; 或者将符号检验与随机检验进行交错进行;
3. 采用先验知识,探索以往容易出错的函数;目前也有研究通过AI的方式得到这些推荐的分析路径;
· 利用完善的程序分析技术(Sound program analysis techniques): 这种方法主要是使用程序分析和软件验证中的各种思想,以合理的方式降低路径探索的复杂性。
1. 静态地合并路径,然后再求解;
2. 通过函数摘要,缓存或重用已经计算过的信息用于后续的计算中;
3. 通过剪枝,去除无关的变量对路径的求解的影响;
5.2. 约束求解(Constraint Solving)
尽管在过去的几年中,约束解决方案技术取得了长足的进步,但约束求解是符号执行的技术瓶颈。
· 减少不相关的约束(Irrelevant constraint elimination) 符号执行中的绝大多数查询是为了确定某个分支的可行性,一种有效的优化方法是从路径条件中删除与当前分支的结果无关的那些约束。
· 增量求解(incremental solving) 符号执行期间生成的约束集的一个重要特征是,它们根据来自程序源代码的一组固定的静态分支来表示。因此,许多路径具有相似的约束集,因此可以采用相似的解决方案。
1. 通过重用先前类似查询的结果,来提高约束求解的速度;
2. 通过约束集的超集,减少无解的情况出现; 我们目前常用的符号执行的工具KLEE,在设计中都采用了着两种方式。
5.3. 内存建模(Memory Modeling)
在符号执行中我们将变量映射到了一个内存模型,来表示这个变量的类型、值或者值域。这个对变量的抽象模式对程序语句转化成符号约束的精度和对符号执行的覆盖率有着很大的影响。太过精确,往往容易陷入复杂的计算,而不能得到具体的解;太过笼统,又会造成漏报。所以精度和可扩展性之间是需要权衡的。
目前这个权衡的主要参考依据是:
1. 具体分析问题的性质;
2. 采用的约束求解器的限制;
6. 符号执行工具
下面列举了我们常用的符号执行工具作为大家的参考。
| 语言 | 符号执行器 | 链接 | 备注信息 |
|---|---|---|---|
| LLVM | KLEE | https://klee.github.io/ | Cadar et al., 2006 |
| LLVM | Cloud9 | http://cloud9.epfl.ch/ | Bucur et al., 2011,基于KLEE的并行符号执行 |
| LLVM | Kite | http://www.cs.ubc.ca/labs/isd/Projects/Kite/ | do Val, 2014, 基于KLEE |
| Java | JPF-Symbc | https://github.com/SymbolicPathFinder/jpf-symbc | 2008, 用于测试NASA的软件 |
| Java | jayhorn | http://jayhorn.github.io/jayhorn/ | 基于soot,支持Z3, 2016 |
| Java | JDart | https://github.com/psycopaths/jdart | Luckow et al., 2016 |
| Python | PyExZ3 | https://github.com/thomasjball/PyExZ3 | Ball and Daniel,2015 |
| JavaScript | Jalangi | https://github.com/Samsung/jalangi2 | Sen et al., 2013 |
| Binaries | angr | http://angr.io/ | Shoshitaishvili et al., 2015, python框架 |
7. 结束语
目前符号执行,在实际的应用中还主要用于与fuzz结合使用,用于缩小fuzz的取值范围。由于符号执行的主要瓶颈--约束求解的性能和局限性,并未在静态分析的商业工具中,大规模的使用。但我们有理由相信,在不久的将来随着并行技术、计算性能的提升、以及求解器的优化,符号执行能够在静态分析中发挥越来越大的作用。
8. 参考文献
[1] King JC. Symbolic execution and program testing. Communications of the ACM, 1976,19(7):385−394.
[2] Cadar C, Sen K. Symbolic execution for software testing: three decades later[J]. Communications of the ACM, 2013, 56(2): 82-90.
[3] Baldoni R, Coppa E, D’elia D C, et al. A survey of symbolic execution techniques[J]. ACM Computing Surveys (CSUR), 2018, 51(3): 50.
[4] Sang Kil Cha, Thanassis Avgerinos, Alexandre Rebert and David Brumley. Unleashing Mayhem on Binary Code. 2012 IEEE Symposium on Security and Privacy.
[5] P. Godefroid, N. Klarlund, and K. Sen. DART: Directed Automated Random Testing. In PLDI’05, June 2005.
[6] K. Sen, D. Marinov, and G. Agha. CUTE: A concolic unit testing engine for C. In ESEC/FSE’05, Sep 2005.、
[7] C. Cadar and D. Engler. Execution generated test cases: How to make systems code crash itself (invited paper). In SPIN’05,Aug 2005.
[8] 百度百科:程序静态分析 https://baike.baidu.com/item/程序静态分析
[9] C. Cadar, D. Dunbar, and D. Engler. KLEE: Unassisted and automatic generation of high-coverage tests for complex systems programs. In OSDI’08, Dec 2008.
[10] L. De Moura and N. Bjørner. Satisfiability modulo theories: introduction and applications. Commun. ACM, 54:69–77, Sept. 2011.
[11] 叶志斌,严波. 符号执行研究综述[J]. 计算机科学, 2018, 45(6A): 28-35.



