非线性声学回声如何破解?华为云硬核技术为你解决
摘要:本文将从非线性声学回声消除产生的原因、研究现状、技术难点出发,详细介绍华为云音视频团队推出的双耦合的声学回声消除算法以及实验检验结果。
非线性的声学回声消除问题,在实际声学系统里面非常普遍也非常棘手,到目前为止还没有特别有效的办法来解决。目前介绍非线性声学回声消除的公开文献也少之又少。华为云专注音视频行业20多年,是如何处理非线性声学回声消除的,效果又如何?华为云音视频专家范展,将从非线性声学回声消除产生的原因、研究现状、技术难点出发,详细介绍华为云音视频团队推出的双耦合的声学回声消除算法以及实验检验结果。以下为分享速记内容:
开篇:为什么分享非线性声学回声消除技术
今天要讲的内容是《非线性声学回声消除技术》,之所以选择这样的方向,主要是基于两个方面的原因:第一非线性的声学回声消除问题是一个困扰了行业很多年的技术难题,这个问题在实际的声学系统里非常普遍,同时又很棘手,到目前为止,还没有特别有效的办法。猜测大家应该会对这个课题感兴趣。
还有另外一个原因,之前做过一些技术的调研,在现有公开的文献资料里,介绍非线性声学回声消除方面的资料非常少,所以想借这样一个机会,介绍一些华为云在这个领域的最新进展,希望能够对大家后续的研究有一些帮助,同时也想跟各位专家做一下技术交流。
今天介绍的内容包括四个部分:
1、第一部分什么是非线性声学回声,它产生的原理、研究现状以及技术难点等问题;
2、第二部分重点介绍双耦合声学回声消除算法;
3、第三部分是通过实验来检验这个算法的性能;
4、最后再做一些简单的总结。
一、非线性声学回声
1.什么是非线性的声学回声
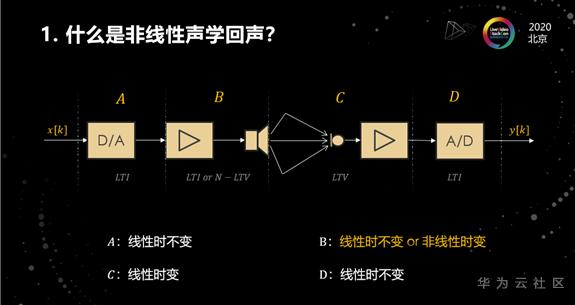
下面直接进入到第一个部分,什么是非线性的声学回声?这里给出了一张图,代表的是声学回声的路径图,图的左边对应的是发射端,右边对应的是接收端。我们发出的信号首先要经过D/A变换,从数字域变换到模拟域,然后再经过功率放大器,放大之后驱动喇叭,这样就会发出声音。发出来的声音经过空气信道传播之后,到了接收端被麦克风采集到,然后再次经过功率放大器,最后再通过A/D变换,从模拟域又变回到数字域。那么这里的y[k]就是我们收到的回声信号。
2.如何判断线性回声和非线性回声
那么问题来了,我们接收到的回声y[k]到底是线性回声还是非线性回声呢?或者说我们应该怎么去判断它?
我觉得要解决这个问题,核心就是要认识清楚这里面的每一个环节,看看它们到底是线性系统还是非线性系统,如果所有的环节都是线性的话,那么很自然y[k]就是一个线性的回声,否则只要有一个环节是非线性的,那么这个回声就是非线性回声。
在这里我将整个回声路径分成了A、B、C、D四个部分。我们一起来看一下,ABCD里面哪一个环节最有可能是非线性的?答案应该是B。也就是回声路径里面的功率放大器和喇叭,具体的原因稍后会做详细分析。
接下来想再解释一下为什么A、C、D它们不是非线性的。首先这里的A和D比较好判断,他们都属于线性时不变系统。比较难判断的是C,因为在一些比较复杂的场景下,声学回声往往会经过多个不同路径的多次反射之后到达接收端,同时会带有很强的混响,甚至在更极端情况下,喇叭与麦克风之间还会产生相对位移变化,导致回声路径也会随时间快速变化。这么多因素叠加在一起,往往会导致回声消除算法的性能急剧退化,甚至完全失效。
有同学可能会问,难道这么复杂的情况,不是非线性的吗?我认为C应该是一个线性时变的声学系统,因为我们区分线性跟非线性的主要依据是叠加原理,前面提到的这些复杂场景,它们依然是满足叠加原理的,所以C是线性系统。
这里还要再补充一点,细心的朋友会发现B里面有一个功率放大器,同时在C里面也有一个功率放大器,为什么经B的功率放大器放大之后,可能带来非线性失真,而C的功率放大器不会产生非线性失真呢?二者的主要区别在于B放大之后输出是一个大信号,用来驱动喇叭。而C放大之后输出依然是小信号,通常不会产生非线性的失真。
3.非线性声学回声产生的原因

非线性声学回声产生的原因,我一共列了两条原因。原因之一,声学器件的小型化与廉价化,这里所指的声学器件就是前面B里面提到的功率放大器和喇叭。
为什么声学器件的小型化容易产生非线性的失真呢?这个需要从喇叭发声的基本原理说起,我们都知道声波的本质是一种物理振动,而喇叭发声的基本原理就是通过电流来驱动喇叭的振膜发生振动之后,这个振膜会带动周围的空气分子相应发生振动,这样就产生了声音。如果我们要发出一个大的声音的话,那么就需要在单位时间内用更多的电流去驱动更多的空气分子发生振动。
假设有大小不同的两个喇叭,他们用同样的功率去驱动,对于大喇叭而言,由于它跟空气接触的面积要大一些,所以他在单位时间内能够带动更多的空气分子振动,所以它发出来的声音也会大一些。而小喇叭如果想发出跟大喇叭一样大的声音,就需要加大驱动功率,这样会带来一个问题:我们的功率放大器件会进入到一种饱和失真的状态,由此就会带来非线性的失真。这就是声学器件小型化容易产生非线性失真的一个主要的原因。 这里廉价化比较好理解了,就不多说了。
原因之二,就是声学结构设计的不合理。最典型的一个实例就是声学系统的隔振设计不合理。喇叭发声单元跟麦克接收单元之间,通常是需要做隔振处理的,如果没有隔振处理的话,那么在喇叭发声的过程中,他所产生的振动会通过物理方式传递到麦克接收端,对麦克接收到的声学信号进行调制,而这种振动本质上是一种随机的、非线性的振动,所以它必然会带来非线性失真。

我们之前针对市面上主要的手机机型做过一次调研,主要调查声学特性。结果我们很惊讶地发现,市面上超过半数的手机机型,声学特性不够理想,对应这里面的“较差”和“极差”这两档。我们平时用手机开外音玩游戏,或者语音通话时,经常会出现漏回声问题和双讲剪切问题,就与手机声学特性不佳有直接联系。
当然这组数据只是针对手机这种电子产品,市面上类似于手机这样的电子产品还有很多,它们应该也有类似的问题。这组数据告诉我们,非线性失真问题在我们生活中的电子产品里是一个普遍存在的问题,我相信对这个问题的研究将会是一个很有价值也很有意义的方向。
4、非线性声学回声消除技术研究现状
之前在IEEE的数字图书馆里搜索了“声学回声消除”的相关文献,最后一共找到了3402篇,其中有会议论文,还有期刊、杂志、书等。我用同样的方法搜索了“非线性声学回声消除”,结果只找到了254篇文献,不到前面文献的1/10,这意味着非线性声学回声消除技术在整个声学回声消除领域是一个相对比较冷的研究方向。
既然这个方向很有价值也很有意义,为什么又这么冷呢?我能想到的一个答案是它太难了,非常有挑战性。 下面就来看一下它的技术难点。
5、非线性声学回声消除的技术难点
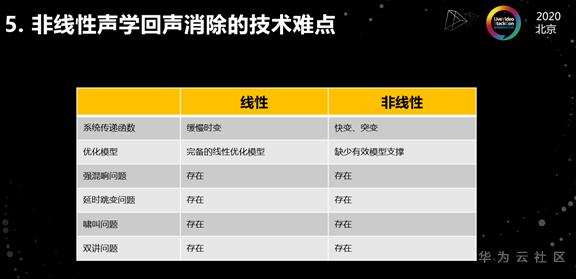
我从6个不同的维度比较了线性和非线性这两种回声消除问题。第一个维度,系统传递函数。在线性系统里面,我们认为系统传递函数是一个缓慢时变的系统,我们可以通过自适应滤波的方式去逼近这个传递函数,来有效抑制回声。而在非线性系统里面,系统传递函数通常是快变、突变的,我们如果用线性的方法去逼近的话,会出现滤波器的更新速度,跟不上系统传递函数变化的速度,就会导致声学回声消除不理想。
第二个维度是优化模型,在线性里面我们是有一套非常完备的线性优化模型,从目标函数的构建到系统优化问题的求解,整个脉络是很清晰的。而在非线性的系统里面,目前是缺少一种有效的模型来对它进行支撑的。
接下来的四个维度对应4个问题,它们是线性回声消除领域普遍存在的4个难点问题,这些问题在非线性领域也同样存在。比如强混响问题,我们如果在一个小型会议室里开视频会议,那么声音会经过多次墙壁反射,带来很强的混响,混响的拖尾时间会很长。如果想抑制这样的强混响回声,就需要把线性滤波器的长度加长,这样会带来一个新的问题:按照Widrow的自适应滤波理论,滤波器的长度越长,其收敛速度越慢,同时权噪声越大,进而导致强混响下回声消除不够理想。
第二个问题是延时跳变问题。在实时音视频通话领域,延时跳变是一个比较普遍的问题。主要现象是麦克端采集的信号和回声参考信号之间的时延关系会发生跳变,每次跳变之后就需要重新对齐信号,就会漏一些回声出来。
第三个问题是啸叫问题。啸叫的检测和啸叫的抑制是公认的在回声领域的经典难题。
最后还有双讲问题。双讲是评估回声消除算法性能的一个重要指标,当然也是很难处理的一个问题,因为双讲很容易导致滤波器系数发散。
综合以上这些维度我们可以看到,非线性的声学回声消除是一个很有挑战的研究方向。
二、双耦合声学回声消除算法
这个是我们团队提出来的一种算法,它的主要特点是,在构建滤波器模型的过程中结合了非线性声学回声的一些特性,因此它在抑制非线性回声方面,也体现出固有的优势。
1、非线性声学回声系统建模
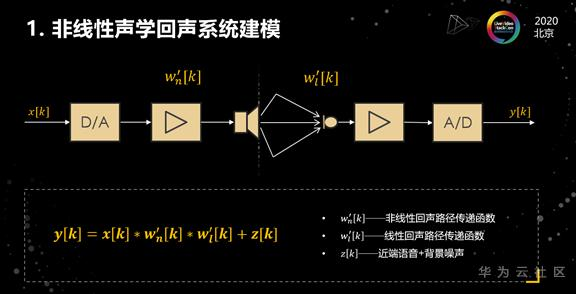
继续回到前面的这个声学回声路径图。我们对这个模型进行了简化。我们将左边的喇叭端用一个传递函数Wn来表示,假设它代表的是非线性的回声路径传递函数;同时我们将喇叭右边,就是麦克端,统一用Wl来表示,他代表的是线性回声传递函数。基于这样的数学假设,我们收到的信号y就可以表示成发射的信号x分别跟这样两个传递函数进行卷积之后的结果。
接下来我们对这个模型进行了适当的简化,简化主要是基于数学分解,我们假设非线性的传递函数,可以分解成线性跟非线性这样两个系统函数的组合形式,就会得到中间的方程。
接下来对中间的方程进行变量替换,就得到最后这个表达式,这个表达式它的物理意义很清晰,我们可以看到,整个回声路径是可以表示成线性回声路径跟非线性回声路径二者之和的形式,这是它的物理意义。
2、双耦合自适应滤波器
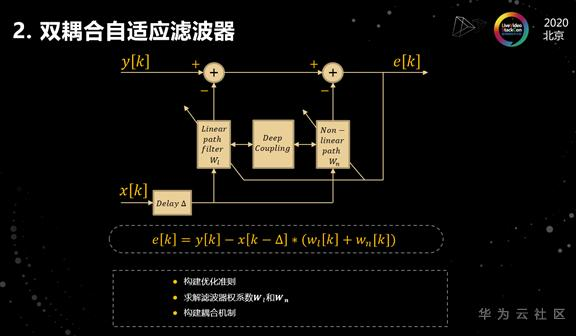
基于这样一个数学模型,接下来我们就构建了一种新的滤波器结构,称之为双耦合自适应滤波器。这个滤波器跟传统线性的自适应滤波器相比,主要有两个方面的不同,第一个不同是传统的线性滤波器只有一个学习单元,而我们的这个滤波器有两个学习单元,分别是这里的线性回声路径滤波器,我们用Wl来表示。还有非线性的回声路径滤波器,我们用Wn来表示。
第二个不同就是,我们在这两个滤波器之间还加入了一个耦合因子,这个耦合因子目的就是为了协同二者更好的工作,让二者能够发挥出最大的效能,甚至能够起到1+1>2的效果。
3、双耦合滤波器设计
当滤波器的结构确定下来之后,我们要去设计滤波器系数了。设计过程我把它总结成了三步,第一步就是构建优化准则,第二步是求解滤波器的权系数——Wl和Wn,最后一步就是构建耦合机制。
第一步就是构建优化准则。我觉得构建优化准则,应该是整个滤波器设计里面最重要的一步,因为它决定了滤波器性能的上限。什么样的优化准则是一个好的优化准则呢?我觉得好的优化准则需要跟问题的物理特性有效匹配起来,所以在构建优化准则之前,我们先对非线性声学回声的特性进行分析,希望通过这种分析去挖掘非线性声学回声的一些物理特性。

我们的分析是基于上面的函数,我们称它为短时相关度,它所表示的是两个信号,在一个短时的观测时间窗“T”这样一个尺度范围内的波形的相似程度,需要注意的是这个函数它是统计意义上的,因为我们对它进行了数学期望运算。同时在分子的最后一项我们还加了一个相位校正因子,目的是为了将这两路信号的初始相位对齐。
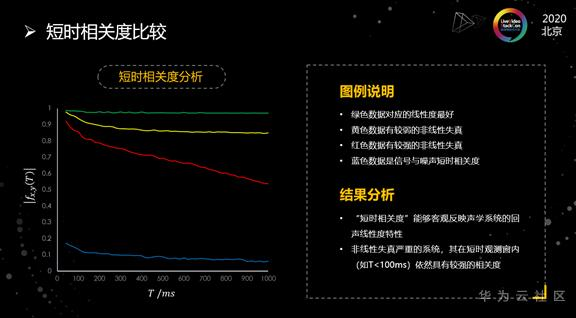
基于前面构建的短时相关度函数,我们对大量声学回声数据进行分析,并挑选了几组比较典型的数据:绿色的曲线对应的是一组线性度非常好的回声数据。我们从这个数据上可以看到,在整个时间T的变化范围内,它的短时相关度都非常高,达到0.97以上,接近于1。黄色曲线,对应的数据具有比较弱的非线性失真,所以在时间T变大了之后,短期相关度逐渐降低,最后趋于一个相对平稳的值。而红色曲线是我们选的一条具有强非线性失真的数据,为了对这三组数据进行有效对比,我们还给出了一条蓝色曲线,这条曲线是信号与噪声的短时相关度,它在整个时间T范围内都很小。
通过这样一组曲线的对比,会得到两个结论,第一个结论就是我们构建的短时相关度函数,能够相对客观反映这个声学系统的线性度特征,线性度越好,这个值会越大。第二个结论:对于非线性失真很强的系统,其在短时观测窗内(如T<100ms)依然具有较强的相关度,这从红色的曲线可以看出来。

也正是基于这样的特征,我们接下来就构建了一种新的误差函数,称之为“短时累积误差函数”。大家可以注意到我们在一个观测时间窗T内,对残差进行了累积。

基于这样的误差函数,我们进一步构建了一种新的优化准则,称为“最小平均短时累计误差准则”。我们希望通过优化准则的约束,最后得到的滤波器权系数能够满足两个特性,第一个特性是滤波器在统计意义上能够达到最优,即全局最优,因此我们在目标函数里加入了数学期望运算。同时,我们还希望它在一个短时的观测时间窗的尺度里面也是最优的,即局部最优,所以在数学期望内部,我们又对误差进行了短时积分。
这个优化准则跟传统的线性自适应滤波器是有本质区别的,因为传统的线性自适应滤波器基于最小均方误差准则,它只是在统计意义上最优,没有局部最优约束。
4、双耦合滤波器设计

首先来求解这里的Wl,就是线性滤波器。主要求解方法是,假设Wn就是非线性滤波器是最优解,把这个最优解代入到前面的优化方程里,就会得到上面简化之后的优化目标函数。
在这个地方,我们又做了一些先验假设,假设非线性的滤波器的一阶统计量和二阶统计量都等于0,我们就可以把上面的优化问题进一步简化,就得到我们非常熟悉的方程,就是Wiener-Hopf方程。这个结果告诉我们,线性滤波器的最优解跟传统的自适应滤波器的最优解是一致的,都是Wiener-Hopf 方程的理论最优解。所以我们就可以采用一些现有的比较成熟的算法,比如NLMS算法、RLS算法,对它进行迭代求解。 这就是Wl的设计。

接下来再看看Wn的设计。Wn的设计跟Wl的设计是类似的,也是需要将优化之后的线性滤波器,代入到最开始的优化问题里,可以把前面的优化问题简化成下面的方程。接下来进行一系列的变量替换之后,最后就得到了非线性滤波器的最优解,它具有最小二乘估计形式。

第三步构建耦合机制。 在介绍耦合机制之前,先说一下我对这种耦合机制的期望特性。我希望在声学系统的线性度非常好的情况下,线性滤波器起到主导作用,而非线性滤波器处于休眠的状态,或者关闭的状态;反过来,当声学系统的非线性很强时,希望非线性滤波器起到主导作用,而线性滤波器处于半休眠状态。实际声学系统往往是非线性与线性两种状态的不断交替、叠加,因此我们希望构建一种机制来对这两种状态进行耦合控制。
为了设计耦合机制,就必须对线性度和非线性度特征进行度量。因此,我们定义了两个因子,分别是线性度因子和非线性度因子,对应左边的这两个方程。而我们进行耦合控制的基本思想就是将这两个因子的值代入到 NLMS算法和最小二乘算法之中,调整二者的学习速度。
为了便于大家对双耦合声学回声消除算法有一个定性的认识,我又画了一组曲线,左边一组图对应的是线性回声的场景。我们首先来看一下NLMS算法,黄色曲线代表真实的系统传递函数,红色曲线是NLMS算法的结果。可以看到,在线性场景下,NLMS算法得到的线性滤波器可以有效逼近真实传递函数,进而能够有效抑制线性声学回声。
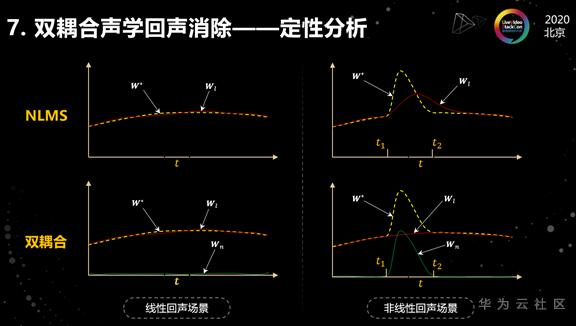
下面再来看一下这个双耦合算法,在线性的回声场景里,双耦合的非线性滤波器是处于休眠的状态,所以它的值是趋于0的,这个时候起主导作用的是线性滤波器。
接下来我们再看一下右边的非线性声学回声场景。我们假设非线性的失真主要出现在t1到t2这个时间段内,大家可以看到黄色线在这个时间里,出现了一次突变,对于NLMS算法,当出现非线性失真之后,它的线性滤波器会去逼近非线性失真。但是由于学习的速度跟不上滤波器变化的速度,所以它跟真实的值之间总是存在一个比较大的gap。 同时当非线性失真消失之后,它还需要一段时间恢复到正常状态,因此在整个时间段里,都会出现回声泄露的问题。
接下来我们再看双耦合算法,在非线性失真出现之后,线性滤波器会进入到一种相对休眠的状态,就是前面所提到的耦合机制,会降低它的更新速度,所以在整个非线性出现的这段时间里,他的值是缓慢变化的。
进入非线性失真状态之后,非线性滤波器开始工作,它会快速跟踪非线性特性的变化,而当非线性失真消失之后,非线性滤波器又进入休眠状态。将这两个滤波器结合起来,就可以实现对整个声学回声路径的变化进行有效跟踪。这里只是给出了一个示例,实际情况往往要复杂很多。
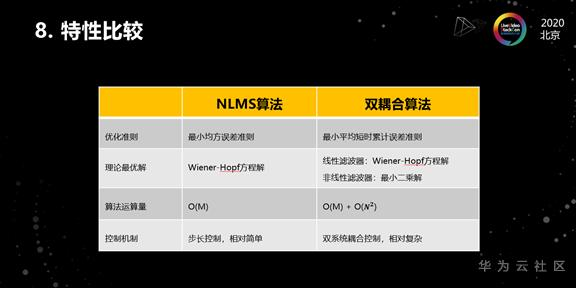
接下来我们对这2个滤波器做了特性比较,主要是从4个不同的维度。首先是优化准则。NLMS算法是基于最小均方误差准则,而双耦合算法是基于最小平均短时累计误差准则,所以他们的优化准则是不一样的。
第二个就是理论的最优解,NLMS算法具有Wiener-Hopf方程解,而双耦合算法的线性滤波器也具有Wiener-Hopf方程解,非线性滤波器具有最小二乘解。
第三个维度就是运算量,NLMS运算量是O(M),M代表是滤波器的阶数,而双耦合算法运算量后面会多一个O(N2),因为他有两个滤波器,N是非线性滤波器的阶数,这里的平方是因为最小二乘需要对矩阵进行求逆运算,所以它的运算量比线性的NLMS运算量要大很多。
第三个就是控制机制,NLMS算法只有一个滤波器,它的控制主要是通过调整步长来实现的,控制起来要相对简单。而双耦合算法需要对两套滤波器进行耦合控制,控制的复杂度要高很多。
三、实验结果分析
这里我主要是分了两个实验场景比较双耦合算法和NLMS算法的性能,第一个是单讲测试场景,第二个就是双讲测试场景。
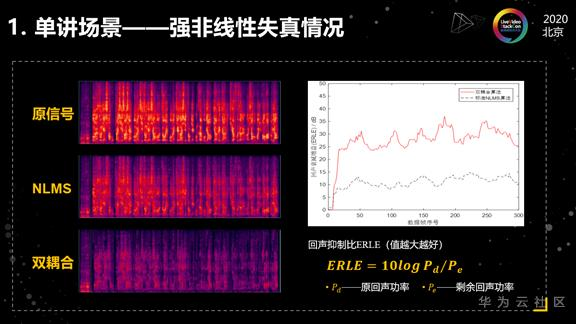
首先看一下单讲测试场景,第一个示例是针对强非线性失真的情况,左边三幅图分别代表原信号的语谱图, NLMS算法进行回声消除之后的语谱图、双耦合算法的语谱图。颜色越深,代表能量越大。右边这个图代表的是回声抑制比,值越大越好,红色的曲线是双耦合算法的回声抑制比,黑色这条线是标准NLMS算法的回声抑制比。
我们可以看到,NLMS算法在收敛之后,回声抑制比只能到10个分贝左右,相对比较低。而双耦合算法在收敛之后,可以达到25个分贝以上,也就是说它比NLMS算法多15个分贝,这个优势是很明显的。
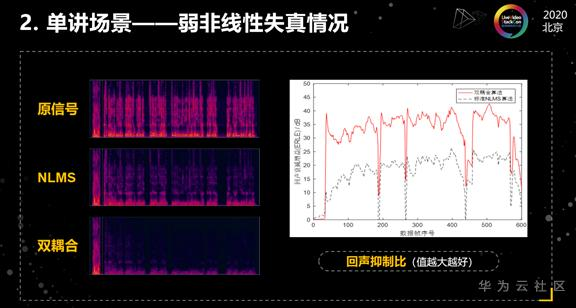
接下来我们再看第二个示例,针对弱非线性失真的情况,左边是语谱图,右边是回声抑制比。我们评估单讲性能的主要指标是回声抑制比和收敛速度。首先看一下NLMS算法,它在收敛之后,大概可以抑制22~25个分贝。这个算法的收敛速度很慢,大概经过100多帧之后才会进入到相对收敛的状态。
再来看一下双耦合算法,在稳定之后,可以抑制35~40个分贝,比NLMS算法大概提升15~20个分贝的回声抑制比。 同时它还有一个很明显的优势:收敛速度很快,几乎是回声到了之后,他瞬间就进入到收敛状态。
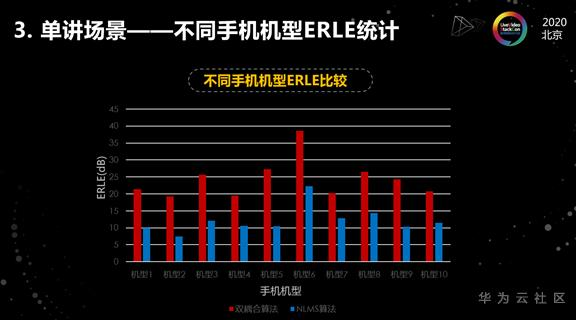
接下来这个图是针对不同手机机型的回声抑制比的比较。红色是双耦合算法,蓝色是NLMS算法,从这组数据里面,我们可以看到双耦合算法比NLMS算法普遍提升了大概10个分贝以上的回声抑制比,具有比较大的优势。
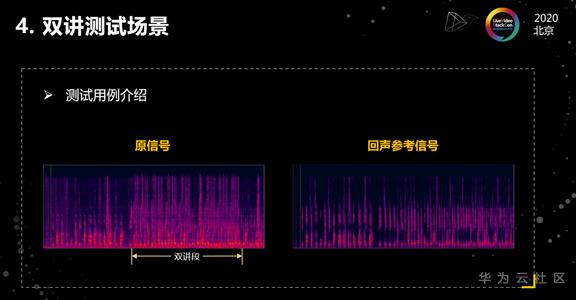
最后再进入双讲测试场景。我首先介绍一下测试的示例,这组数据是一个视频会议的数据,左边这个图是原始的麦克信号语谱图,右边这个图是回声参考信号语谱图,我们比较这两个图之后就会发现,双讲段主要出现在中间这一段。
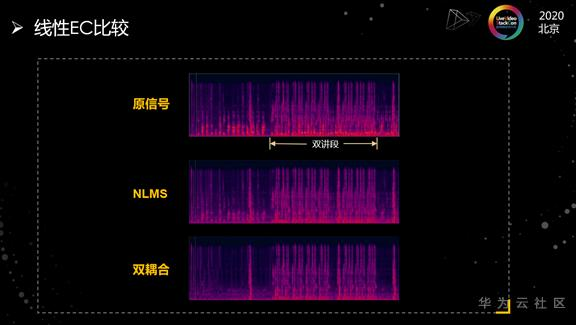
我们评估双讲性能的主要指标是回声抑制比和近端语音失真度。上面这三幅图是经过回声消除之后的语谱图,中间的图是NLMS算法的结果。我们可以看到它的回声抑制不是很理想,不管在单讲段还是在双讲段,都有比较多的回声残留。而最下面这个图是采用双耦合算法得到的语谱图,可以看到在单讲和双讲里面回声抑制得都比较干净,并且在双讲里,对近端语音的损伤也很小。这个数据对应视频会议场景,因此还需要做最后一步NLP的处理。
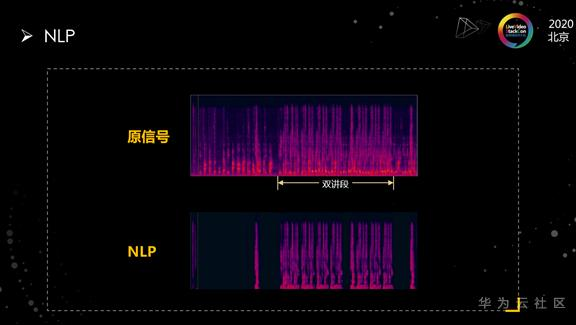
上面这个图就是基于双耦合算法,做了NLP之后的输出结果。我们可以看到处理完之后,整个语谱很清晰,回声去得很干净,而且语谱没有太大损伤,双讲很通透。
四、总结

最后我再来简单总结一下,今天主要是介绍了三个方面的内容,第一个就是认识了非线性声学回声、产生的原因、研究现状以及技术难点。
接下来重点介绍了华为云音视频的双耦合声学回声消除算法,我们的主要贡献体现在两个方面,第一个方面就是构建一种双耦合自适应滤波器结构;第二个就是提出了最小平均短时累计误差准则并进行求解。通过求解之后,我们会得到双耦合滤波器的线性滤波器是具有Wiener-Hopf方程解的最优解这种形式,然后非线性滤波器具有最小二乘解。
最后我们通过实验来检验这个算法的性能,发现他在强非线性失真的场景下,线性场景下,还有双讲场景下均取得了明显的性能提升;回声抑制比提高了10个分贝以上;收敛速度更快,大概在30毫秒以内。但这个算法也有缺陷:运算量偏大;耦合控制环节比较多,相对要复杂一些。



