【华为云技术分享】7 分钟全面了解位运算

位运算是我们在编程中常会遇到的操作，但仍然有很多开发者并不了解位运算，这就导致在遇到位运算时会“打退堂鼓”。实际上，位运算并没有那么复杂，只要我们了解其运算基础和运算符的运算规则，就能够掌握位运算的知识。接下来，我们一起学习位运算的相关知识。

程序中的数在计算机内存中都是以二进制的形式存在的，位运算就是直接对整数在内存中对应的二进制位进行操作。

注意：本文只讨论整数运算，小数运算不在本文研究之列

位运算的基础

我们常用的 3， 5 等数字是十进制表示，而位运算的基础是二进制。即人类采用十进制，机器采用的是二进制，要深入了解位运算，就需要了解十进制和二进制的转换方法和对应关系。

二进制

十进制转二进制时，采用“除 2 取余，逆序排列”法：

1. 用 2 整除十进制数，得到商和余数;
2. 再用 2 整除商，得到新的商和余数;
3. 重复第 1 和第 2 步，直到商为 0;
4. 将先得到的余数作为二进制数的高位，后得到的余数作为二进制数的低位，依次排序;

排序结果就是该十进制数的二进制表示。例如十进制数 101 转换为二进制数的计算过程如下：

101 % 2 = 50 余 1
50 % 2 = 25 余 0
25 % 2 = 12 余 1
12 % 2 = 6 余 0
6 % 2 = 3 余 0
3 % 2 = 1 余 1
1 % 2 = 0 余 1

逆序排列即二进制中的从高位到低位排序，得到 7 位二进制数为 1100101，如果要转换为 8 位二进制数，就需要在最高位补 0。即十进制数的 8 位二进制数为 01100101。

其完整过程如下图所示：

有网友整理了常见的进制与 ASCII 码对照表，表内容如下：

ASCII 控制字符

ASCII 可显示字符

补码

现在，我们已经了解到二进制与十进制的换算方法，并拥有了进制对照表。但在开始学习位运算符之前，我们还需要了解补码的知识。

数值有正负之分，那么仅有 0 和 1 的二进制如何表示正负呢？

人们设定，二进制中最高位为 0 代表正，为 1 则代表负。例如 0000 1100 对应的十进制为 12，而 1000 1100 对应的十进制为 -12。这种表示被称作原码。但新的问题出现了，原本二进制的最高位始终为 0，为了表示正负又多出了 1，在执行运算时就会出错。举个例子，1 + (-2) 的二进制运算如下：

0000 0001 + 1000 0010 
= 1000 0011
= -3 

这显然是有问题的，问题就处在这个代表正负的最高位。接着，人们又弄出了反码（二进制各位置的 0 与 1 互换，例如 0000 1100 的反码为 1111 0011）。此时，运算就会变成这样：

0000 0001 + 1111 1101
= 1111 1110
# 在转换成十进制前，需要再次反码
= 1000 0001 
= -1

这次好像正确了。但它仍然有例外，我们来看一下 1 + (-1)：

0000 0001 + 1111 + 1110
= 1111 1111
= 1000 0000
= -0

零是没有正负之分的，为了解决这个问题，就搞出了补码的概念。补码是为了让负数变成能够加的正数，所以 负数的补码= 负数的绝对值取反 + 1，例如 -1 的补码为：

-1 的绝对值 1
= 0000 0001 # 1 的二进制原码
= 1111 1110 # 原码取反
= 1111 1111 # +1 后得到补码

-1 补码推导的完整过程如下图所示：

反过来，由补码推导原码的过程为 原码 = 补码 - 1，再求反。要注意的是，反码过程中，最高位的值不变，这样才能够保证结果的正负不会出错。例如 1 + (-6) 和 1 + (-9) 的运算过程如下：

# 1 的补码 + -6 的补码
0000 0001 + 1111 1010
= 1111 1011 # 补码运算结果
= 1111 1010 # 对补码减 1，得到反码
= 1000 0101 # 反码取反，得到原码
= -5 # 对应的十进制
# 1 的补码 + -9 的补码
0000 0001 + 1111 0111
= 1111 1000 # 补码运算结果
= 1111 0111 # 对补码减 1，得到反码
= 1000 1000 # 反码取反，得到原码
= -8 # 对应的十进制

要注意的是，正数的补码与原码相同，不需要额外运算。也可以说，补码的出现就是为了解决负数运算时的符号问题。

人生苦短 我用 Python。

崔庆才|静觅 邀请你关注微信公众号：进击的Coder

运算符介绍

位运算分为 6 种，它们是：

名称	符号
按位与	&
按位或	|
按位异或	^
按位取反	~
左移运算	<<
右移运算	>>

按位与

按位与运算将参与运算的两数对应的二进制位相与，当对应的二进制位均为 1 时，结果位为 1，否则结果位为 0。按位与运算的运算符为 &，参与运算的数以补码方式出现。举个例子，将数字 5 和数字 8 进行按位与运算，其实是将数字 5 对应的二进制 0000 0101 和数字 8 对应的二进制 0000 1000 进行按位与运算，即：

0000 0101
&
0000 1000

根据按位与的规则，将各个位置的数进行比对。运算过程如下：

0000 0101
&
0000 1000
---- ----
0000 0000

由于它们对应位置中没有“均为 1 ”的情况，所以得到的结果是 0000 0000。数字 5 和 8 按位与运算的完整过程如下图：

将结果换算成十进制，得到 0，即 5&8 = 0。

按位或

按位或运算将参与运算的两数对应的二进制位相或，只要对应的二进制位中有 1，结果位为 1，否则结果位为 0。按位或运算的运算符为 |，参与运算的数以补码方式出现。举个例子，将数字 3 和数字 7 进行按位或运算，其实是将数字 3 对应的二进制 0000 0011和数字 7 对应的二进制 0000 0111 进行按位或运算，即：

0000 0011
|
0000 0111

根据按位或的规则，将各个位置的数进行比对。运算过程如下：

0000 0011
|
0000 0111
---- ----
0000 0111

最终得到的结果为 0000 0111。将结果换算成十进制，得到 7，即 3|7 = 7。

按位异或

按位异或运算将参与运算的两数对应的二进制位相异或，当对应的二进制位值不同时，结果位为 1，否则结果位为 0。按位异或的运算符为 ^，参与运算的数以补码方式出现。举个例子，将数字 12 和数字 7 进行按位异或运算，其实是将数字 12 对应的二进制 0000 1100 和数字 7 对应的二进制 0000 0111 进行按位异或运算，即：

0000 1100
^
0000 0111

根据按位异或的规则，将各个位置的数进行比对。运算过程如下：

0000 1100
^
0000 0111
---- ----
0000 1011

最终得到的结果为 0000 1011。将结果换算成十进制，得到 11，即 12^7 = 11。

按位取反

按位取反运算将二进制数的每一个位上面的 0 换成 1，1 换成 0。按位取反的运算符为 ~，参与运算的数以补码方式出现。举个例子，对数字 9 进行按位取反运算，其实是将数字 9 对应的二进制 0000 1001 进行按位取反运算，即：

～0000 1001
= 0000 1001 # 补码，正数补码即原码
= 1111 1010 # 取反
= -10

最终得到的结果为 -10。再来看一个例子，-20 按位取反的过程如下：

～0001 0100
= 1110 1100 # 补码
= 0001 0011 # 取反
= 19

最终得到的结果为 19。我们从示例中找到了规律，按位取反的结果用数学公式表示：

我们可以将其套用在 9 和 -20 上：

～9 = -(9 + 1) = -10
~(-20) = -((-20) + 1) = 19

这个规律也可以作用于数字 0 上，即 ~0 = -(0 + 1) = -1。

左移运算

左移运算将数对应的二进位全部向左移动若干位，高位丢弃，低位补 0。左移运算的运算符为 <<。举个例子，将数字 5 左移 4 位，其实是将数字 5 对应的二进制 0000 0101 中的二进位向左移动 4 位，即：

5 << 4
= 0000 0101 << 4
= 0101 0000 # 高位丢弃，低位补 0
= 80

数字 5 左移 4 位的完整运算过程如下图：

最终结果为 80。这等效于:

也就是说，左移运算的规律为：

右移运算

右移运算将数对应的二进位全部向右移动若干位。对于左边的空位，如果是正数则补 0，负数可能补 0 或 1 （Turbo C 和很多编译器选择补 1）。右移运算的运算符为 >>。举个例子，将数字 80 右移 4 位，其实是将数字 80 对应的二进制 0101 0000 中的二进位向右移动 4 位，即：

80 >> 4
= 0101 0000 >> 4
= 0000 0101 # 正数补0，负数补1 
= 5

最终结果为 5。这等效于：

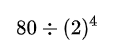
也就是说，右移运算的规律为：

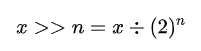
要注意的是，不能整除时，取整数。这中除法取整的规则类似于 PYTHON 语言中的地板除。

位运算的应用

在掌握了位运算的知识后，我们可以在开发中尝试使用它。坊间一直流传着位运算的效率高，速度快，但从未见过文献证明，所以本文不讨论效率和速度的问题。如果正在阅读文章的你有相关文献，请留言告知，谢谢。

判断数字奇偶

通常，我们会通过取余来判断数字是奇数还是偶数。例如判断 101 的奇偶用的方法是：

# python
if 101 % 2:
    print('偶数')
else:
    print('奇数')

我们也可以通过位运算中的按位与来实现奇偶判断，例如：

# python
if 101 & 1:
    print('奇数')
else:
    print('偶数')

这是因为奇数的二进制最低位始终为 1，而偶数的二进制最低为始终为 0。所以，无论任何奇数与 1 即 0000 0001 相与得到的都是 1，任何偶数与其相与得到的都是 0。

变量交换

在 C 语言中，两个变量的交换必须通过第三个变量来实现。伪代码如下：

# 伪代码
a = 3, b = 5
c = a
a = b
b = a
--------
a = 5, b = 3

在 PYTHON 语言中并没有这么麻烦，可以直接交换。对应的 PYTHON 代码如下：

# python
a, b = 3, 5
a, b = b, a
print(a, b)

代码运行结果为 5 3。但大部分编程语言都不支持 PYTHON 这种写法，在这种情况下我们可以通过位运算中的按位异或来实现变量的交换。对应的伪代码如下：

# 伪代码
a = 3, b = 5
a = a ^ b
b = a ^ b
a = a ^ b

最后，a = 5, b = 3。我们可以用 C 语言和 PYTHON 语言进行验证，对应的 PYTHON 代码如下：

# python
a, b = 3, 5
a = a ^ b
b = a ^ b
a = a ^ b
print(a, b)

代码运行结果为 5 3，说明变量交换成功。对应的 C 代码如下：

#include<stdio.h>
void main()
{
    int a = 3, b = 5;
    printf("交换前：a=%d , b=%d\n",a,b);
    a = a^b;
    b = a^b;
    a = a^b;
    printf("交换后：a=%d , b=%d\n",a, b);           
} 

代码运行结果如下：

交换前：a=3 , b=5
交换后：a=5 , b=3

这说明变量交换成功。

求 x 与 2 的 n 次方乘积

设一个数为 x，求 x 与 2 的 n 次方乘积。这用数学来计算都是非常简单的：

在位运算中，要实现这个需求只需要用到左移运算，即 x << n。

取 x 的第 k 位

即取数字 x 对应的二进制的第 k 位上的二进制值。假设数字为 5，其对应的二进制为 0000 0101，取第 k 位二进制值的位运算为 x >> k & 1。我们可以用 PYTHON 代码进行验证：

# python
x = 5  # 0000 0101
for i in range(8):
    print(x >> i & 1)

代码运行结果如下：

1
0
1
0
0
0
0
0

这说明位运算的算法是正确的，可以满足我们的需求。

判断赋值

if a == x:
    x = b
else:
    x = a

等效于 x = a ^ b ^ x。我们可以通过 PYTHON 代码来验证：

# python
a, b, x = 6, 9, 6
if a == x:
    x = b
else:
    x = a
print(a, b, x)

代码运行结果为 699，与之等效的代码如下：

# python
a, b, x = 6, 9, 6
x = a ^ b ^ x
print(a, b, x)

这样就省去了 if else 的判断语句。

代替地板除

二分查找是最常用的算法之一，但它有一定的前提条件：二分查找的目标必须采用顺序存储结构，且元素有序排列。例如 PYTHON 中的有序列表。二分查找的最优复杂度为 O(1)，最差时间复杂度为 O(log n)。举个例子，假设我们需要从列表 [1, 3, 5, 6, 7, 8, 12, 22, 23, 43, 65, 76, 90, 543] 中找到指定元素的下标，对应的 PYTHON 代码如下：

# python
def search(lis: list, x: int) -> int:
    """非递归二分查找
    返回指定元素在列表中的索引
    -1 代表不存在"""
    mix_index = 0
    max_index = len(lis) - 1
    while mix_index <= max_index:
        midpoint = (mix_index + max_index) // 2
        if lis[midpoint] < x:
            mix_index = mix_index + 1
        elif lis[midpoint] > x:
            max_index = max_index - 1
        else:
            return midpoint
    return -1


lists = [1, 3, 5, 6, 7, 8, 12, 22, 23, 43, 65, 76, 90, 543]
res = search(lists, 76)
print(res)

在取列表中间值时使用的语句是 midpoint = (mix_index + max_index) // 2，即地板除，我们可以将其替换为 midpoint = (mix_index + max_index) >> 1 最终得到的结果是相同的。这是因为左移 1位 等效于乘以 2，而右移 1 位等效于除以 2。这样的案例还有很多，此处不再赘述。

至此，我们已经对位运算有了一定的了解，希望你在工作中使用位运算。

作者：华为云云享专家 韦世东