深度学习在其他领域的应用1：密码破解

近年来，深度学习在人体感知方面（如视觉、听觉和理解）的应用有着显著的效果，许多人也跃跃欲试将其应用到传统领域，希望能给这些领域带来改变。老山也打算发表一个系列，历数深度学习在其他领域的应用。本系列不定期更新，不保证不太监，各个领域老山也只能管中窥豹，不全面、不准确之处还请大家谅解。

话题

本期的话题是深度学习能否用于密码破解呢？

老山的答案是不能，或者是不实际。当然所有解答的前提是概念范畴的统一，为了说明这个问题，我们从基础开始，逐步说明原因。

前馈神经网络的实质

在本节中，撇开了前馈神经网络的生物意义，着眼于其数学理论。对于样本集(xi,yi) xi∈X, yi∈Y，其中X,Y分别是输入域和输出域。机器学习的目的寻找函数f:X→Y使得f(xi)=yi成立或者更好的成立。比如对于猫狗分类问题，就是去寻找函数f，使得f(猫图片1)=猫,...。而神经网络作为机器学习的方法的一种，无非是给定了函数f的构造方法。我们下面就从神经元开始，讲解前馈神经网络如何进行函数构造。

对于单层的第j个神经元，我们有：

对于整个单层，写成矩阵形式，有：

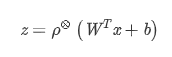
对于简单的前馈神经网络，最终构造函数为各层函数的复合函数：

其中是激活函数ρ，是让构造函数增加非线性部分的。没有激活函数，最终构造函数是线性函数的复合函数，仍然是线性函数。所以激活函数的基本要求是非线性。但对于常见的激活函数，如sigmoid函数和ReLU函数，除了非线性外，一般还都是连续函数，所以最终构造的函数也具有连续性。

universal approximation theorem证明了对于绝大多数激活函数（包括如sigmoid函数之类的任意有界非恒常的连续函数，或者ReLU函数），函数集f(x) = ∑αj ρ(Wj x+bj)集在指定紧空间稠密，也就是说即便是单层网络，只要给定足够的节点，构造函数能近似任意连续函数。

这给定了深度学习网络的数学背景。证明过程涉及了许多泛函理论的知识，结果乍看上去比较神奇，但其实是相对平凡的。事实上，我们可以用折线来逼近任意曲线，只要折线的控制点足够多。我们也可以使用样条函数、基函数等方式去逼近任意连续函数。这些方法也可以用于构造函数。

激活函数选用如sigmoid函数这样的光滑函数，最终的生成函数也是光滑的。而选用ReLU函数这样的分段线性函数，最终的生成函数也是分段线性的，但函数本身也是连续的，所有的间断点都是第一类间断点，在二维的表现就是一个折线。

可以简单证明，对于L层，每层宽度均为w的前馈神经网络，生成函数的第一类间断点数最多为(2w)^L，其中2是ReLU函数的片段数。由此，可以得知，增加深度比增加宽度能更好的提高函数的曲折能力，能更快的近似到给定函数上。当然，由于控制参数总数为Lw^2远小于最多间断点数，这也意味着要么大部分生成的函数并没有如此多的间断点，要么这些曲折中有大量重复的模式。而这是深度学习网络能解决的函数范围，连续而有规律的函数。

密码学

传统的密码破解意思在已知加密方式的前提下，给定足够的明文 (plaintext) 和密文 (ciphertext)，能否根据给定的密文去破解得到相应的明文。听起来很有点像对抗神经网络的感觉。把明文密文弄成样本集，构造深度学习网络意味着构造一个从明文到密文的函数f，来模拟加密算法c。

如前所述，深度学习网络乃至机器学习的生成函数通常都是分段光滑的，数据间存在着规律和特征。而现代加密算法要么基于大量的离散函数变换，要么基于一些难以计算的数论问题（如素数分解、椭圆曲线计算等），使得输出的密文与真实随机数据在统计意义上无法被区分。一个好的加密算法，破坏了输入输出之间的规律和模式，很难用机器学习来获取，而深度学习网络去模拟，其控制参数也要与其秘钥集相当，这无异于暴力破解。

当然，这前提都是面对的加密算法足够的好，确实破坏了输入输出之间的规律和模式。但考虑到AES加密方法的代数结构十分简单，而RSA等方法所基于的数论问题或许还是存在着一些未被了解清楚的离散规则，即便如此，使用以光滑函数为基础的深度学习网络去模拟离散函数的规律仍然并不好用。

深度学习不适合于密码算法的破解，也并不意味着不能用于密码破解。PassGAN便是通过深度学习来挖掘用户密码明文的分布规律来生成破解密码进行攻击的，但与密码算法破解本身无关。

后记

为一件事下结论需要的不仅仅是勇气，而是调查和研究这个事的时间和精力。为了这篇短文，老山查阅了许多文献，也思考了很多，感觉比写之前的文章累的多了。如果您有不同看法，也欢迎和老山交流。

作者：山找海味