无重复元素的排列

/*==========================================================
设有n个整数的集合{1,2,3，......,n}，从中任意选择r个数进行排列。
其中r<n，请列出所有排列。

思路：递归r层，每层选择一个数放到a[]。当递归到r层时得到一组排列。
在每一层中做选择的时候，要把所有可能的选择都进行尝试。
具体看代码。
============================================================*/

#include <stdio.h>
#include <stdlib.h>
int num=0,a[10001]={0},n,r;
int b[10001]={0};     // a[]是选择的r个数，b[i]是标志i是否已经被选中
//假如，待选择的n个数并非1~n，而是c[]中的n元素。则a[]保存被选中的数的下标即可。

void search(int k);//递归r层，每层选择一个数放到a[]。当递归到r层时得到一组排列
void print();      //输出一组排列的方案

int main()
{
    scanf("%d%d",&n,&r);
    search(1);
    printf("总的方案数：%d\n",num);
    return 0;
}
void search(int k)//递归r层，每层选择一个数放到a[]。当递归到r层时得到一组排列
{
    int i;
    for(i=1;i<=n;i++)
    {
        if(b[i]==0)
        {
            a[k]=i; //选择i作为第k个数字
            b[i]=1; //标识i已经被使用过
            if(k==r) { num++; print(); }//得到一个方案，则方案数加1并输出方案。
            else search(k+1);           //尚未找够r个数字，继续寻找第k+1个数字
            b[i]=0; //还原现场：标识i没被使用过。
        }
    }
}
void print()       //输出一组排列的方案
{
    int i;
    for(i=1;i<=r;i++)
        printf("%d ",a[i]);
    printf("\n");
}

 

缺陷：
（1）这里只能是固定地选择1~n中的r个数字，不是输入的n个数字中选r个。
（2）n个数字不能有重复的元素存在

对缺陷（1），可以考虑把n个数字放在c[]，然后a[]存储被选中的元素的下标。
例如a[i]=x表示c[x]被选中。b[i]=1表示c[i]被选中。
这样一来，在选择判断的时候使用b[],在输出的时候使用a[]。

对缺陷（2），可以看看“有重复元素的排列”.

上面的代码是可以生成遵守字典序的全排列的。
下面的算法效率较高，但是不符合严格的字典序：
来源：https://subetter.com/

#include <iostream>
#include <algorithm>
using namespace std;
void FullPermutation(int array[], int left, int right)
{
    if (left == right)
    {
        for (int i = 0; i < 4; i++)
            cout << array[i] << " ";
        cout << endl;
    }
    else
    {
        for (int i = left; i <= right; i++)
        {
            swap(array[i], array[left]);
            FullPermutation(array, left + 1, right);
            swap(array[i], array[left]);
        }
    }
}
int main()
{
    int array[4] = { 1,2,3,4 };
    FullPermutation(array, 0, 3);
    return 0;
}

利用C++算法库函数实现全排列

（下面的内容是原作者整理的。）

熟悉 C++ 的朋友肯定知道另一种更简单，更完美的全排列方法。

定义于文件 <algorithm> 内的两个算法函数：

• next_permutation，对于当前的排列，如果在字典序中还存在下一个排列，返回真，并且把当前排列调整为下一个排列；如果不存在，就把当前排列调整为字典序中的第一个排列（即递增排列），返回假。
• prev_permutation，对于当前的排列，如果在字典序中还存在上一个排列，返回真，并且把当前排列调整为上一个排列；如果不存在，就把当前排列调整为字典序中的最后一个排列（即递减排列），返回假。

/**
 *
 * author : 刘毅（Limer）
 * date   : 2017-05-31
 * mode   : C++
 */
#include <iostream>  
#include <algorithm>  
using namespace std;
void FullPermutation(int array[])
{
    do
    {
        for (int i = 0; i < 4; i++)
            cout << array[i] << " ";
        cout << endl;
    } while (next_permutation(array, array + 4));
}
int main()
{
    int array[4] = { 1,2,3,4 };
    FullPermutation(array);
    return 0;
}

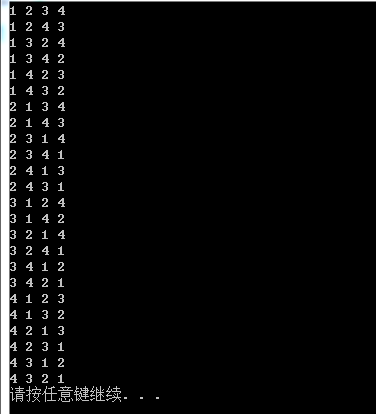
运行结果：