【递归练习】放苹果
http://www.cnblogs.com/dongsheng/archive/2012/08/15/2640468.html
Description
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
Input
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
Output
对输入的每组数据M和N,用一行输出相应的K。
Sample Input
1 7 3
Sample Output
8

/* 功能Function Description: POJ-1664 开发环境Environment: DEV C++ 4.9.9.1 技术特点Technique: 版本Version: 作者Author: 可笑痴狂 日期Date: 20120815 备注Notes: 解题分析: 设f(m,n) 为m个苹果,n个盘子的放法数目,则先对n作讨论, 当n>m:必定有n-m个盘子永远空着,去掉它们对摆放苹果方法数目不产生影响。即if(n>m) f(m,n) = f(m,m) 当n<=m:不同的放法可以分成两类: 1、有至少一个盘子空着,即相当于f(m,n) = f(m,n-1); 2、所有盘子都有苹果,相当于可以从每个盘子中拿掉一个苹果,不影响不同放法的数目,即f(m,n) = f(m-n,n). 而总的放苹果的放法数目等于两者的和,即 f(m,n) =f(m,n-1)+f(m-n,n) 递归出口条件说明: 当n=1时,所有苹果都必须放在一个盘子里,所以返回1; 当没有苹果可放时,定义为1种放法。因为: 递归的两条路,第一条n会逐渐减少,终会到达出口n==1; 第二条m会逐渐减少,因为n>m时,我们会return f(m,m) 所以终会到达出口m==0. */ #include<stdio.h> int fun(int m,int n) //m个苹果放在n个盘子中共有几种方法 { if(m==0||n==1) //因为我们总是让m>=n来求解的,所以m-n>=0,所以让m=0时候结束,如果改为m=1, return 1; //则可能出现m-n=0的情况从而不能得到正确解 if(n>m) return fun(m,m); else return fun(m,n-1)+fun(m-n,n); } int main() { int T,m,n; scanf("%d",&T); while(T--) { scanf("%d%d",&m,&n); printf("%d\n",fun(m,n)); } }
如果将终止条件改为m==1||n==1,下面举一个例子说明无限递归的形成过程:
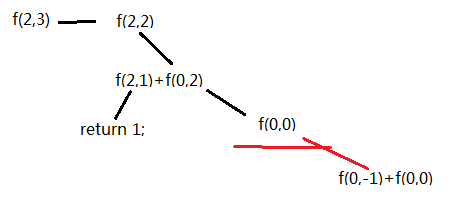
==========================================================================
后来在其他地方看到了一个与此题相同的但问题的情景稍微改变了一下:
把m个同样的球放到n个同样的袋子里面,允许有的袋子空着不放,问共有多少种不同的放置方法?(用K表示)
例如:m=7,n=3,则k=8;这里认为(5,1,1)和(1,5,1)是同一种放置方法。
ps:差一点没认出这个题的面目来……
另一种思路:递推或说动规吧
1 #include <stdio.h> 2 #include <string.h> 3 #define maxM 11 4 #define maxN 11 5 int D[maxM][maxN]={0}; 6 int main(int argc, char *argv[]) 7 { 8 int t,i,j,k,M,N,res; 9 scanf("%d",&t); 10 for(k=0;k<t;k++) 11 { 12 scanf("%d%d",&M,&N); 13 memset(D,0,sizeof(D[0][0])*maxM*maxN); 14 //D[i][j]表示把i个果放进j个盘子 15 for(j=1;j<=N;j++) D[1][j]=1; 16 for(i=1;i<=M;i++) D[i][1]=1; 17 for(i=2;i<=M;i++) 18 { 19 for(j=2;j<=N;j++) 20 { 21 if(i<j) D[i][j]= D[i][i]; 22 else if(i>j) D[i][j]=D[i-j][j]+D[i][j-1]; 23 else D[i][j]=1+D[i][j-1]; // i==j的情况 24 } 25 } 26 printf("%d\n",D[M][N]); 27 } 28 return 0; 29 }
学生学习回溯算法时,设计的一个算法,挺有新意的:
by韦泽鸿:
1 #include <iostream> 2 using namespace std; 3 int k=0,m,n; 4 int ans[20]={0}; 5 void Print(){ 6 cout<<ans[0]; 7 for(int i=1;i<n;i++) 8 cout<<' '<<ans[i]; 9 cout<<endl; 10 } 11 void dfs(int t,int x,int num){//第t个盘,已经用了x个,这一次至少要用num个 12 if(t==n) { 13 if(x==m) {k++;/*Print();*/} 14 return; 15 } 16 for(int i=num;x+i<=m;i++){ 17 ans[t]=i; 18 dfs(t+1,x+i,i); 19 ans[t]=0; 20 } 21 } 22 int main(){ 23 int t; 24 cin>>t; 25 while(t--){ 26 cin>>m>>n; 27 dfs(0,0,0); 28 cout<<k<<endl; 29 k=0; 30 } 31 return 0; 32 }






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· 单线程的Redis速度为什么快?