P3382 【模板】三分法

题目链接

强烈建议跟二分法计算函数零点的这道题目做对比。

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5
1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

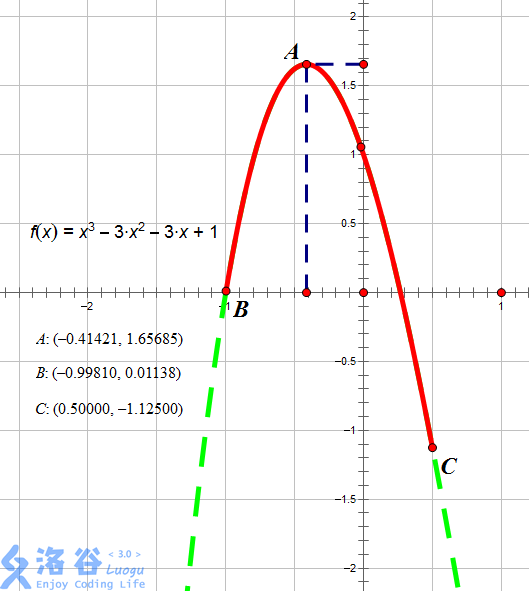
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

（Tip.l&r的范围并不是非常大ww不会超过一位数）

 

算法分析

如题所述，就是用三分算法直接套模板即可。

所谓三分算法我是在曹文老师的《信息学奥赛一本通·提高篇》分治算法章节首次接触。原文如下图所示。

下面是本题的AC代码：

#include<stdio.h>
#include<math.h>
int N;
double a[20];
double f(double x)
{
    double res=0;
    int i;
    for(i=N;i>=0;i--) res=res+a[i]*pow(x,i);
    return res;
}
int main()
{
    freopen("p3382.in","r",stdin);
    int i;
    double L,R,m1,m2;
    double t1,t2;
    scanf("%d%lf%lf",&N,&L,&R);
    for(i=N;i>=0;i--) scanf("%lf",&a[i]);
    while(L+1e-6<R)
    {
        m1=L+(R-L)/3; m2=R-(R-L)/3;
        t1=f(m1);  t2=f(m2);
        if(t1<t2) L=m1;
        else R=m2;
    }
    printf("%.5lf",L);
    return 0;
}