【题解】洛谷P1502 窗口的星星

Des

晚上，小卡从阳台望出去，“哇~~~~好多星星啊”，但他还没给其他房间设一个窗户。

天真的小卡总是希望能够在晚上能看到最多最亮的星星，但是窗子的大小是固定的，边也必须和地面平行。

这时小卡使用了超能力（透视术）知道了墙后面每个星星的位置和亮度，但是小卡发动超能力后就很疲劳，只好拜托你告诉他最多能够有总和多亮的星星能出现在窗口上。

\(\texttt{Data Range:}\)

\(1\le T \le 10\)

\(1\le n \le 10^4\)

\(1\le W,H \le 10^6\)

\(0\le x_i,y_i < 2^{31}\)

Sol

考虑把「星星在窗子所在的矩形中」转化为「窗子的右上角在星星上面 H，右边 W 的矩形中」。这样就可以把整个问题转化为找一个点使得覆盖该点的矩形最多。

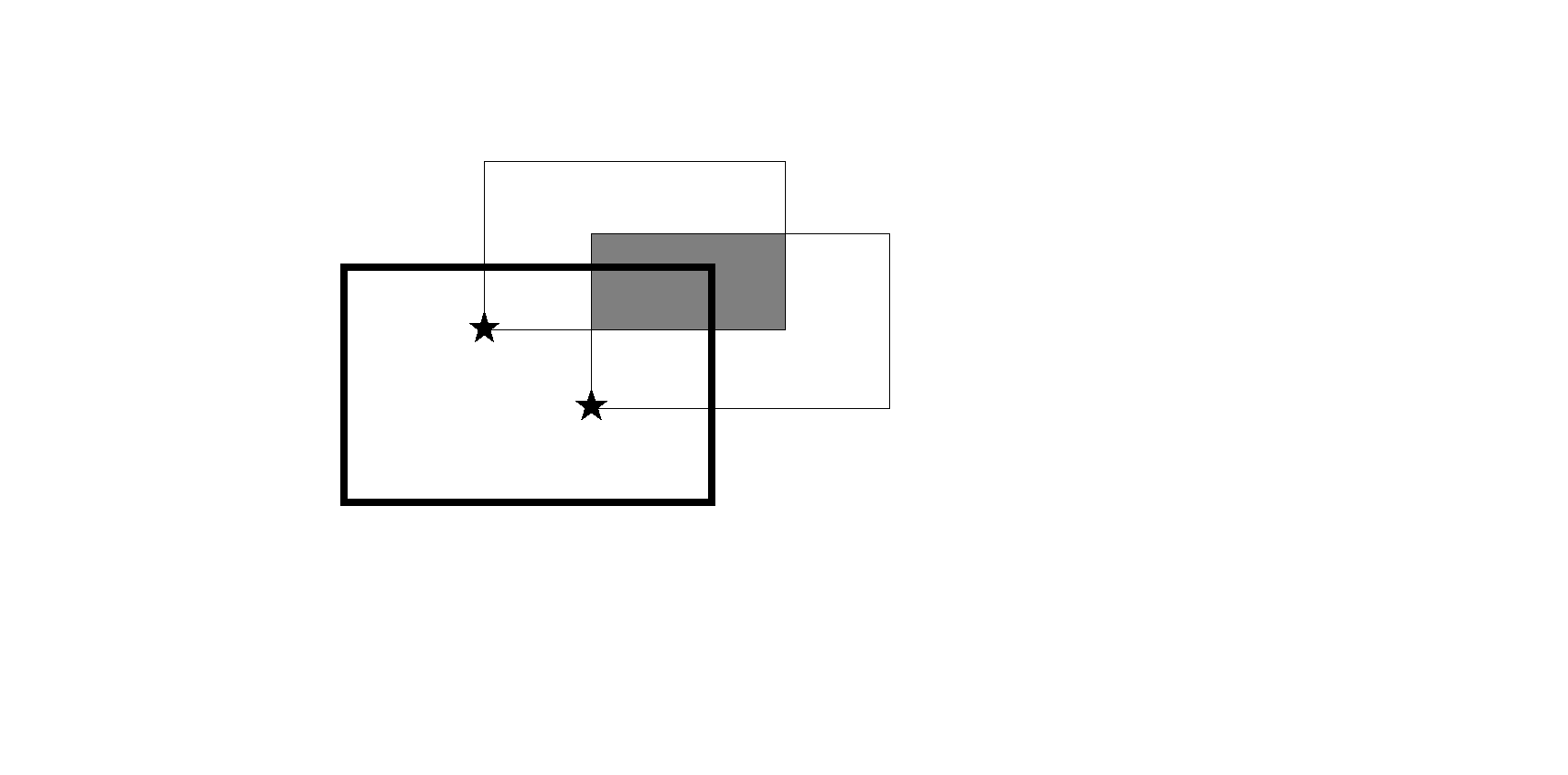
（如图，矩形框住了两个星星）

现在考虑窗户边框的限制。

如图，虽然窗户的右上角不能落在黑框上，只能落在黑框里，但将黑框的长和宽的两端都减小一个 eps（极小值）得到红框后，窗户的右上角就可以落在红框里的任何一个地方了。

但是如果减小 eps，星星所对应的矩形的坐标就变成了实数。

这时出现了一种方法，将矩形的长宽在两端都减小 0.5，然后把坐标轴向上平移、向右平移 0.5 个单位。最后生成的矩形左下角是 \((x,y)\)，右上角是 \(x+W-1,y+H-1\)。

这样做为什么是正确的呢？长宽减小的数值需要保证原本有交的矩形仍然有交。由于星星的坐标是整数，所以极限情况（可能会在矩形缩小后没有交的情况）如下图：

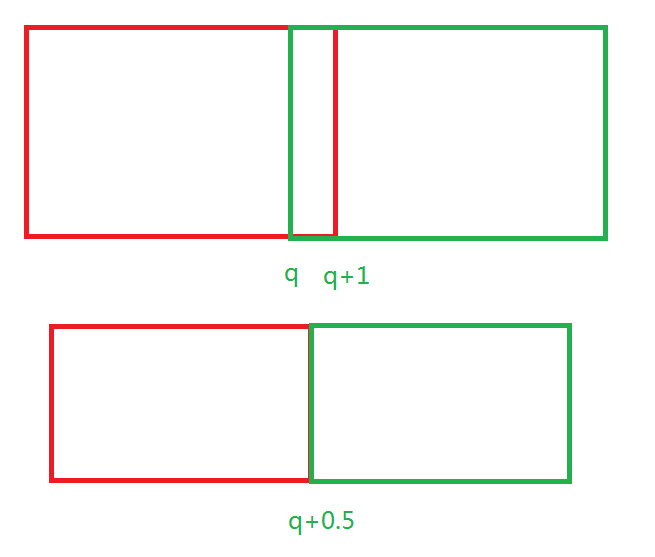
在减小 0.5 之后仍然有交（只不过在对 line 进行排序的时候需要把 l 为正的排在前面）。而两端减小 0.5，合起来就是 1，这导致生成的矩形在平移坐标轴之后的坐标可以是整数。

所以这其实是一个很巧妙的方法，很多题解没说清楚。

My code

和模板不一样，这道题线段树上的点映射到的就是平面上的点。

const int N = 2e4 + 10;
int T, n, W, H, stc, ans, v[N];
struct node {
	int x, ya, yb, k;
	bool operator<(const node &b) { return x < b.x || (x == b.x && k > b.k); }
} a[N];

struct segmentTree {
	#define lc(x) (x << 1)
	#define rc(x) (x << 1 | 1)
	int mx[N << 2], tag[N << 2];
	void pdown(int p) {
		if(tag[p]) {			
			mx[lc(p)] += tag[p], mx[rc(p)] += tag[p];
			tag[lc(p)] += tag[p], tag[rc(p)] += tag[p];
			tag[p] = 0;
		}
	}
	void modify(int l, int r, int p, int x, int y, int k) {
		if(l >= x && r <= y) {
			mx[p] += k, tag[p] += k;
			return;
		}
		pdown(p);
		int mid = (l + r) >> 1;
		if(x <= mid) modify(l, mid, lc(p), x, y, k);
		if(y > mid) modify(mid + 1, r, rc(p), x, y, k);
		mx[p] = max(mx[lc(p)], mx[rc(p)]);
	}
	#undef lc
	#undef rc
} st;

inline int find(int x) {
	return lower_bound(v + 1, v + stc + 1, x) - v;
}

void clear() {
	stc = 0, ans = 0;
	memset(st.mx, 0, sizeof st.mx);
	memset(st.tag, 0, sizeof st.tag);
}

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr);
	for(cin >> T; T; T--) {
		cin >> n >> W >> H;
		clear();
		for(int i = 1, x, y, l; i <= n; i++) {
			cin >> x >> y >> l;
			a[2 * i - 1] = node{x, y, y + H - 1, l};
			a[2 * i] = node{x + W - 1, y, y + H - 1, -l};
			v[++stc] = y, v[++stc] = y + H - 1;
		}
		sort(a + 1, a + 2 * n + 1);
		sort(v + 1, v + stc + 1);
		stc = unique(v + 1, v + stc + 1) - v - 1;
		for(int i = 1; i <= n * 2; i++) {
			ans = max(ans, st.mx[1]);
			st.modify(1, stc, 1, find(a[i].ya), find(a[i].yb), a[i].k);
		}
		cout << ans << '\n';
	}

	return 0;
}