【笔记】网络流

好几篇笔记揉在一起的东西 😕

最小割和 Primal-Dual 的部分是最近写的，其他部分是去年写的。

网络与流的概念

网络 $G=(V,E)$ 是一张有向图，每条边 $(u,v)\in E$ 都有一个特殊的权值 $c(u,v)$ ，表示这条边的流量限制。且拥有一条虚拟的反边 $(u,v)'$ 。图中还有两个特殊的节点 $S\in V$ 和 $T\in V(S\ne T)$ ，分别称为源点和汇点。

设 $f(x,y)$ 是定义在二元组 $(x\in V,y\in V)$ 上的实数函数，且满足：

$f(x,y)\le c(x,y)$ 。
$f(x,y)=-f'(x,y)$ 。
$\displaystyle\sum_{(u,x)\in E}f(u,x)=\sum_{(x,y)\in E}f(x,y)$ 。

$f$ 称为网络的流函数， $f(x,y)$ 称为边的流量， $c(x,y)-f(x,y)$ 称为边的剩余容量。 $\sum_{(S,u)\in E}f(S,u)$ 称为整个网络的流量。

对于 $(u,v)\in E$ ，有 $c(u,v)'=0$ 。之所以称 $(u,v)$ 的反边 $(u,v)'$ 是虚拟的，是因为反边并不会有真正的流量经过，只是起一个辅助求解最大流的作用，原理后面会讲到。

最大流

使得整个网络的流量 $\sum_{(S,u)\in E}f(S,u)$ 最大的流函数称作网络的最大流。

Edmonds-Karp

若一条从 $S$ 到 $T$ 的路径上的所有边的剩余容量都大于 0，则称这样的一条路径为增广路。

EK 算法每次通过 BFS 找到一条增广路，并修改增广路上的流量，来达到找到网络最大流的目的。

EK 算法的时间复杂度为 $O(nm^2)$ 。

增广路的算法可以通过下面这张图来理解：

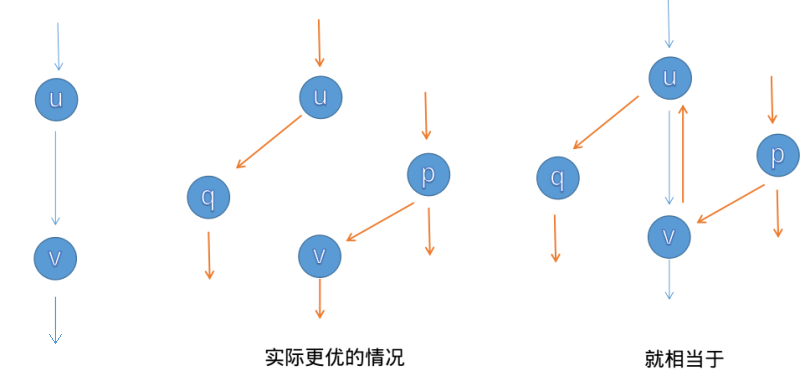
在上图中，最开始 $(u,v)$ 有流量经过，并给反边的虚拟流量 $f'(u,v)$ 设置了一个标记，表示可以有新的流量来代替 $f(u,v)$ ，给 $v$ 传送流量。而从 $p$ 过来的流量经过 $v$ 时，发现了这个标记，于是便走过了 $u$ 和 $q$ 。相当于 $p$ 的流量给了 $v$ ，而 $u$ 原有的流量给了 $q$ 。这就是虚拟边的意义。

Dinic

每次 BFS 只能找到一条增广路，属实有些浪费。

Dinic 算法每次使用 BFS 建出“分层图”，然后使用 DFS 进行多路增广，时间复杂度为 $O(n^2m)$ 。

为了方便起见，对于，Dinic 算法中的反边，定义 $c'(x,y)=c(x,y)$ ， $f'(x,y)=c(x,y)-f(x,y)$ ，并且在初始化时 $f(x,y)=c(x,y)$ 。这样与 [[#网络与流的概念]] 中的定义起到的效果是一样的，但判断一条边是否有剩余容量，只需判断 $f(x,y)$ 是否大于 0 即可，比较方便。许多网络流求解算法也是这样实现的。

最多重新 BFS 建图 $n$ 次，因为每一次需要重新建图时至少有一层已经不能增广。建图后最多增广 $m$ 次，即找到 $m$ 条增广路。每次增广需要 $O(n)$ 的时间。所以总时间复杂度为 $O(n^2m)$ ，注意这是在运用当前弧优化的前提下。

Dinic 算法模板：

struct edges {
	int head[N], nowHead[N], nxt[M], v[M], w[M], cnt;
	void add(int a, int b, int x) { 
		nxt[++cnt] = head[a], head[a] = cnt, v[cnt] = b, w[cnt] = x;
		nxt[++cnt] = head[b], head[b] = cnt, v[cnt] = a, w[cnt] = 0;
	}
	edges() { cnt = 1; }
} g;

namespace MF {
	int S, T, n, maxFlow, flow, maxl = 1e9, d[N];
	queue<int> q;
	bool bfs() {
		for(int i = 1; i <= n; i++) d[i] = 0;
		q.push(S), d[S] = 1;
		while(!q.empty()) {
			int u = q.front();
			q.pop(), g.nowHead[u] = g.head[u];
			for(int i = g.head[u]; i; i = g.nxt[i]) {
				int v = g.v[i];
				if(g.w[i] && !d[v]) {
					d[v] = d[u] + 1;
					q.push(v);
				}
			}
		}
		return d[T];
	}
	int dfs(int u, int flow) {
		if(u == T) return flow;
		int rest = flow;
		for(int i = g.nowHead[u]; i && rest; i = g.nxt[i]) {
			g.nowHead[u] = i;
			int v = g.v[i];
			if(g.w[i] && d[v] == d[u] + 1) {
				int k = dfs(v, min(g.w[i], rest));
				if(!k) d[v] = 0;
				rest -= k, g.w[i] -= k, g.w[i ^ 1] += k;
			}
		}
		return flow - rest;
	}
	int solve() {
		maxFlow = flow = 0;
		while(bfs()) {
			do {
				flow = dfs(S, maxl);
				maxFlow += flow;
			} while(flow);
		}
		return maxFlow;
	}
}

最小割

最大流最小割定理

定理： $f(s,t)_{\max}=c(s,t)_{\min}$

证明：

对于任意一个可行流 $f(s,t)$ 的割 $(S,T)$ ，我们可以得到：

f (s, t) = S 出边的总流量 - S 入边的总流量 \leq S 出边的总流量 = c (s, t)

$f(s,t)=S\text{出边的总流量}-S\text{入边的总流量}\le S\text{出边的总流量}=c(s,t)$

如果我们求出了最大流 $f$ ，那么残余网络中一定不存在 $s$ 到 $t$ 的增广路经，也就是 $S$ 的出边一定是满流， $S$ 的入边一定是零流，于是有：

f (s, t) = S 出边的总流量 - S 入边的总流量 = S 出边的总流量 = c (s, t)

$f(s,t)=S\text{出边的总流量}-S\text{入边的总流量}=S\text{出边的总流量}=c(s,t)$

结合前面的不等式，我们可以知道此时 $f$ 已经达到最大。

模型与应用

经典模型： $n$ 个物品放到两个集合 $A,B$ 。第 $i$ 个物品不放入 $A$ 集合的花费是 $A_i$ ，不放入 $B$ 集合的花费是 $B_i$ 。另有若干个形如 $(u,v,w)$ 的限制，表示如果 $u$ 和 $v$ 如果不放在同一个集合的花费是 $w$ 。求花费的最小值。

将一个点和源点 $S$ 相连视作放入集合 $A$ ，和汇点 $T$ 相连视作放入集合 $B$ 。那么把一些边割开就可以看作时不放入某个集合的代价。于是我们先不考虑 $(u,v,w)$ 的限制，建出如下的粗略模型：

这个图的最小割的含义就是把每个点恰放入一个集合需要的最小花费。

然后考虑加入 $(u,v,w)$ 的限制。首先假设 $1$ 号点放在集合 $A$ ， $2$ 号点放在集合 $B$ ，此时上图中 a2,b1 的边会被割掉。想要此时最小割值增加 $w$ 的话应当连一条（1,2,w）的边。同理， $1$ 号点放在集合 $B$ ， $2$ 号点放在集合 $A$ 的情况应当连一条 (2,1,w) 的边。

似乎加边的工作就做完了。但是，加边会不会导致本来不连通的情况变得连通？并不会。对 1 号点和 2 号点所属集合分类讨论，发现不存在这种情况。

还有一个问题是很多题目给出的条件并不是“不放入集合产生代价”，而是“放入集合产生贡献”。解决方法是先算出一个“理论上界”表示某点可能产生的最大贡献。这个最大贡献可以选较大的那个集合，也甚至可以两个集合都选。其实就是说我们提前钦定了每个点选择集合的方式（甚至可能同时选两个），这种选择集合方式造成的贡献一定要大于等于实际上能产生的最大贡献。然后用最小割把整张图割开使得限制被满足，最小割的值就是需要减掉的最小的贡献。理论上界 - 最小割就是答案（贡献的最大值）。

最小费用最大流

定义

给定一个网络 $G=(V,E)$ ，每条边除了有容量限制 $c(u,v)$ ，还有一个单位流量的费用 $w(u,v)$ 。

当 $(u,v)$ 的流量为 $f(u,v)$ 时，需要花费 $f(u,v)\times w(u,v)$ 的费用。

$w$ 也满足斜对称性，即 $w(u,v)=-w(v,u)$ 。

则该网络中总花费最小的最大流称为 最小费用最大流，即在最大化 $\sum_{(s,v)\in E}f(s,v)$ 的前提下最小化 $\sum_{(u,v)\in E}f(u,v)\times w(u,v)$ 。

SPFA 建图，DFS 多路增广

const int N = 5e3 + 5, E = 1e5 + 5, MAXF = 1e9;
int n, m;
struct edges {
	int head[N], nxt[E], v[E], w[E], c[E], cnt;
	void add(int a, int b, int p, int q) {
		nxt[++cnt] = head[a], head[a] = cnt, v[cnt] = b, w[cnt] = p, c[cnt] = q;
		nxt[++cnt] = head[b], head[b] = cnt, v[cnt] = a, w[cnt] = 0, c[cnt] = -q;
	}
	edges() { cnt = 1; }
} g;
namespace MCMF {
	int n, S, T, maxFlow, minCost, dis[N], inq[N], vis[N];
	deque<int> q;
	bool SPFA() {
		for(int i = 1; i <= n; i++) inq[i] = false, dis[i] = MAXF;
		dis[T] = 0, q.push_back(T);
		while(!q.empty()) {
			int u = q.front();
			q.pop_front(), inq[u] = false;
			for(int i = g.head[u]; i; i = g.nxt[i]) {
				int v = g.v[i];
				if(g.w[i ^ 1] && dis[v] > dis[u] - g.c[i]) {
					dis[v] = dis[u] - g.c[i];
					if(!inq[v]) {
						inq[v] = true, q.push_back(v);
						if(dis[q.front()] > dis[q.back()]) swap(q.front(), q.back());
					}
				}
			}
		}
		return dis[S] < MAXF;
	}
	int dfs(int u, int flow) {
		vis[u] = true;
		if(u == T) return flow;
		int rest = flow;
		for(int i = g.head[u]; i; i = g.nxt[i]) {
			int v = g.v[i];
			if(!vis[v] && g.w[i] && dis[v] == dis[u] - g.c[i]) {
				int k = dfs(v, min(rest, g.w[i]));
				rest -= k, g.w[i] -= k, g.w[i ^ 1] += k;
				minCost += k * g.c[i];
			}
		}
		return flow - rest;
	}
	void solve() {
		maxFlow = minCost = 0;
		while(SPFA()) {
			do {
				for(int i = 1; i <= n; i++) vis[i] = false;
				maxFlow += dfs(S, INT_MAX);
			} while(vis[T]);
		}
	}
}

Primal-Dual

参考：

费用流 - OI Wiki (oi-wiki.org)

本校神仙学长写的博客（vector 存边 + pb_ds 优先队列，巨快）：

「补档计划」最小费用流 Primal Dual 算法 - xehoth

最短路 - OI Wiki (oi-wiki.org)

SSP 算法

一切基于寻找最小费用增广路的费用流算法（包括 Primal-Dual 算法，统称为 SSP 算法）时间复杂度都不可避免带有 $f$ （最大流的流量），而通过构造 $f$ 可以达到 $n$ 的指数级别。

除非题目规定 $f$ 在一个可接受范围内，否则一般费用流的题目的复杂度都是错的。

Primal-Dual 算法的优势在于，当费用都是正的时候，可以直接做到 $O(fm\log m)$ 的复杂度。如果有负权边得先做一次

Johnson 全源最短路

（直接复制的 OI-wiki）：

Johnson 和 Floyd 一样，是一种能求出无负环图上任意两点间最短路径的算法。该算法在 1977 年由 Donald B. Johnson 提出。

任意两点间的最短路可以通过枚举起点，跑 $n$ 次 Bellman-Ford 算法解决，时间复杂度是 $O(n^2m)$ 的，也可以直接用 Floyd 算法解决，时间复杂度为 $O(n^3)$ 。

注意到堆优化的 Dijkstra 算法求单源最短路径的时间复杂度比 Bellman-Ford 更优，如果枚举起点，跑 $n$ 次 Dijkstra 算法，就可以在 $O(nm\log m)$ （取决于 Dijkstra 算法的实现）的时间复杂度内解决本问题，比上述跑 $n$ 次 Bellman-Ford 算法的时间复杂度更优秀，在稀疏图上也比 Floyd 算法的时间复杂度更加优秀。

但 Dijkstra 算法不能正确求解带负权边的最短路，因此我们需要对原图上的边进行预处理，确保所有边的边权均非负。

一种容易想到的方法是给所有边的边权同时加上一个正数 $x$ ，从而让所有边的边权均非负。如果新图上起点到终点的最短路经过了 $k$ 条边，则将最短路减去 $kx$ 即可得到实际最短路。

但这样的方法是错误的。考虑下图：

$1 \to 2$ 的最短路为 $1 \to 5 \to 3 \to 2$ ，长度为 $−2$ 。

但假如我们把每条边的边权加上 $5$ 呢？

新图上 $1 \to 2$ 的最短路为 $1 \to 4 \to 2$ ，已经不是实际的最短路了。

Johnson 算法则通过另外一种方法来给每条边重新标注边权。

我们新建一个虚拟节点（在这里我们就设它的编号为 $0$ ）。从这个点向其他所有点连一条边权为 $0$ 的边。

接下来用 Bellman-Ford 算法求出从 $0$ 号点到其他所有点的最短路，记为 $h_i$ 。

假如存在一条从 $u$ 点到 $v$ 点，边权为 $w$ 的边，则我们将该边的边权重新设置为 $w+h_u-h_v$ 。

接下来以每个点为起点，跑 $n$ 轮 Dijkstra 算法即可求出任意两点间的最短路了。

一开始的 Bellman-Ford 算法并不是时间上的瓶颈，若使用 priority_queue 实现 Dijkstra 算法，该算法的时间复杂度是 $O(nm\log m)$ 。

正确性证明

为什么这样重新标注边权的方式是正确的呢？

在讨论这个问题之前，我们先讨论一个物理概念——势能。

诸如重力势能，电势能这样的势能都有一个特点，势能的变化量只和起点和终点的相对位置有关，而与起点到终点所走的路径无关。

势能还有一个特点，势能的绝对值往往取决于设置的零势能点，但无论将零势能点设置在哪里，两点间势能的差值是一定的。

接下来回到正题。

在重新标记后的图上，从 $s$ 点到 $t$ 点的一条路径 $s \to p_1 \to p_2 \to \dots \to p_k \to t$ 的长度表达式如下：

$(w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+ \dots +(w(p_k,t)+h_{p_k}-h_t)$

化简后得到：

$w(s,p_1)+w(p_1,p_2)+ \dots +w(p_k,t)+h_s-h_t$

无论我们从 $s$ 到 $t$ 走的是哪一条路径， $h_s-h_t$ 的值是不变的，这正与势能的性质相吻合！

为了方便，下面我们就把 $h_i$ 称为 $i$ 点的势能。

上面的新图中 $s \to t$ 的最短路的长度表达式由两部分组成，前面的边权和为原图中 $s \to t$ 的最短路，后面则是两点间的势能差。因为两点间势能的差为定值，因此原图上 $s \to t$ 的最短路与新图上 $s \to t$ 的最短路相对应。

到这里我们的正确性证明已经解决了一半——我们证明了重新标注边权后图上的最短路径仍然是原来的最短路径。接下来我们需要证明新图中所有边的边权非负，因为在非负权图上，Dijkstra 算法能够保证得出正确的结果。

根据三角形不等式，图上任意一边 $(u,v)$ 上两点满足： $h_v \leq h_u + w(u,v)$ 。这条边重新标记后的边权为 $w'(u,v)=w(u,v)+h_u-h_v \geq 0$ 。这样我们证明了新图上的边权均非负。

这样，我们就证明了 Johnson 算法的正确性。

Primal-Dual 原始对偶算法

用 Bellman-Ford 求解最短路的时间复杂度为 $O(nm)$ ，无论在稀疏图上还是稠密图上都不及 Dijkstra 算法。但网络上存在单位费用为负的边，因此无法直接使用 Dijkstra 算法。

Primal-Dual 原始对偶算法的思路与 Johnson 全源最短路径算法类似，通过为每个点设置一个势能，将网络上所有边的费用（下面简称为边权）全部变为非负值，从而可以应用 Dijkstra 算法找出网络上单位费用最小的增广路。

首先跑一次最短路，求出源点到每个点的最短距离（也是该点的初始势能） $h_i$ 。接下来和 Johnson 算法一样，对于一条从 $u$ 到 $v$ ，单位费用为 $w$ 的边，将其边权重置为 $w+h_u-h_v$ 。

可以发现，这样设置势能后新网络上的最短路径和原网络上的最短路径一定对应。证明在介绍 Johnson 算法时已经给出，这里不再展开。

与常规的最短路问题不同的是，每次增广后图的形态会发生变化，这种情况下各点的势能需要更新。

如何更新呢？先给出结论，设增广后从源点到 $i$ 号点的最短距离为 $d'_i$ （这里的距离为重置每条边边权后得到的距离），只需给 $h_i$ 加上 $d'_i$ 即可。下面我们证明，这样更新边权后，图上所有边的边权均为非负。

容易发现，在一轮增广后，由于一些 $(i,j)$ 边在增广路上，残量网络上会相应多出一些 $(j,i)$ 边，且一定会满足 $d'_i+(w(i,j)+h_i-h_j)=d'_j$ （否则 $(i,j)$ 边就不会在增广路上了）。稍作变形后可以得到 $w(j,i)+(h_j+d'_j)-(h_i+d'_i)=0$ 。因此新增的边的边权非负。

而对于原有的边，在增广前， $d'_i+(w(i,j)+h_i-h_j) - d'_j \geq 0$ ，因此 $w(i,j)+(d'_i+h_i)-(d'_j+h_j) \geq 0$ ，即用 $h_i+d'_i$ 作为新势能并不会使 $(i,j)$ 的边权变为负。

综上，增广后所有边的边权均非负，使用 Dijkstra 算法可以正确求出图上的最短路。

Primal-Dual 算法的时间复杂度是 $O(nm+fm\log m)$ （算上 SPFA 的复杂度）， $f$ 指网络里最大流的大小。但一般达不到那个上界，不然很多题理论上是过不了的。

Primal-Dual 算法代码

网上很多实现都是错的，居然每次用 SPFA 重新建图，然后用 DFS 增广。

StudyingFather 的加强版费用流模板还在搞，所以下面的代码交到洛谷弱鸡模板上不能体现出本算法的优越性。

代码（洛谷模板）：

~~别问我为什么这份代码和上面的邻接表写的不一样，问就是跑得更快但有重名风险。。~~

开 O2 只有 500ms 左右，不开则是 2.12s，差距巨大。不过现在的考试都有 O2 了，所以不用 pb_ds 的优先队列也行。

#include <bits/stdc++.h>

using namespace std;
namespace fastIO {
	#define getchar() (S == T && (T = (S = B) + fread(B, 1, 1 << 16, stdin), S == T) ? EOF : *S++)
	char B[1 << 16], *S = B, *T = B;
	template<typename Tp> inline void read(Tp &o) {
		o = 0; bool s = 0; char c = getchar();
		while(c > '9' || c < '0') s |= c == '-', c = getchar();
		while(c >= '0' && c <= '9') o = o * 10 + c - '0', c = getchar();
		if(s) o = -o;
	}
} using fastIO::read;
#define mp make_pair
typedef pair<int, int> pii;
const int N = 5005, E = (5e4 + 5) * 2, MAXD = INT_MAX / 2, MAXF = INT_MAX; // 反向边
int n, m, s, t;
struct MCMF {
	int n, s, t, maxf, minc;
	int vis[N], h[N], dis[N];
	struct edge {
		int v, f, c, nxt;
	} e[E];
	int cnt = 1, hd[N];
	void eadd(int u, int v, int f, int c) { // 同时建正边和反边 
		e[++cnt].v = v, e[cnt].f = f, e[cnt].c = c;
		e[cnt].nxt = hd[u], hd[u] = cnt;
		e[++cnt].v = u, e[cnt].f = 0, e[cnt].c = -c;
		e[cnt].nxt = hd[v], hd[v] = cnt;
	}
	void spfa() {
		queue<int> q;
		for(int i = 1; i <= n; i++) h[i] = MAXD;
		h[s] = 0, vis[s] = 1, q.push(s);
		while(!q.empty()) {
			int u = q.front();
			q.pop(), vis[u] = 0;
			for(int i = hd[u]; i; i = e[i].nxt) {
				int v = e[i].v;
				if(e[i].f && h[v] > h[u] + e[i].c) {
					h[v] = h[u] + e[i].c;
					if(!vis[v]) vis[v] = 1, q.push(v);
				}
			}
		}
	}
	struct path {
		int v, e;
	} p[N];
	struct node {
		int dis, id;
		bool operator<(const node &a) const {
			return dis > a.dis;
		}
	};
	bool dijkstra() {
		priority_queue<node> q;
		for(int i = 1; i <= n; i++) dis[i] = MAXD, vis[i] = false;
		dis[s] = 0, q.push(node{0, s});
		while(!q.empty()) {
			int u = q.top().id;
			q.pop();
			if(vis[u]) continue;
			vis[u] = true;
			for(int i = hd[u]; i; i = e[i].nxt) {
				int v = e[i].v, nc = e[i].c + h[u] - h[v];
				if(e[i].f && dis[v] > dis[u] + nc) {
					dis[v] = dis[u] + nc;
					// 反着记录边 
					p[v].v = u, p[v].e = i;
					if(!vis[v]) q.push(node{dis[v], v});
				}
			}
		}
		return dis[t] != MAXD;
	}
	pair<int, int> solve() {
		spfa();
		while(dijkstra()) {
			int minf = MAXF;
			// 此时 dis[t] 的值为 w(s,p1)+w(p1,p2)+...+(pn,t)+h[s]-h[t]
			// 因此更新后 h[t]=w(s,p1)+w(p1,p2)+...+(pn,t)
			for(int i = 1; i <= n; i++) h[i] += dis[i];
			// 顺着路径走 
			for(int i = t; i != s; i = p[i].v) minf = min(minf, e[p[i].e].f);
			for(int i = t; i != s; i = p[i].v)
				e[p[i].e].f -= minf, e[p[i].e ^ 1].f += minf;
			maxf += minf;
		    minc += minf * h[t];
		}
		return mp(maxf, minc);
	}
} net;

int main() {
	read(n), read(m), read(s), read(t);
	for(int i = 1, u, v, f ,c; i <= m; i++) {
		read(u), read(v), read(f), read(c);
		net.eadd(u, v, f, c);
	}
	net.n = n, net.s = s, net.t = t;
	auto ans = net.solve();
	cout << ans.first << ' ' << ans.second;

	return 0;
}

求出势能，dij，更新势能，计算花费（minf 乘上汇点的势能）

例题

ABC214H Colleting

Des

给定一张有向图。 $K$ 个人可以在图上走，并采集顶点上的数 $X_i$ 。一个点上的数只能被一个人采到。问所有人能采到的数的总和的最大值。

$N,M\le 2\times 10^5$ ， $K\le 10$ ， $1\le X_i\le 10^9$ 。

Sol

首先因为要采集，把每个点拆成入点和出点 $in(i)$ 和 $out(i)$ 。 $in(i)$ 向 $out(i)$ 连一条容量为 $1$ ，费用为 $-X_i$ 的边，再连一条容量为 $k$ ，费用为 $0$ 的边。

然后对于原图中的边 $(u,v)$ ，建边 $(out(u),in(v))$ ，费用为 0，流量为 $k$ 。

建好的图有负环，用 tarjan 把强连通分量缩点，把整个强连通分量里点的权值加在一个点上。然后就缩成了 DAG，但仍然有负权值。如果用 SPFA 跑第一次的最短路复杂度不对。得用拓扑排序。

My Code

#include <bits/stdc++.h>

using namespace std;
namespace fastIO {
	#define getchar() (S == T && (T = (S = B) + fread(B, 1, 1 << 16, stdin), S == T) ? EOF : *S++)
	char B[1 << 16], *S = B, *T = B;
	template<typename Tp> inline void read(Tp &o) {
		o = 0; bool s = 0; char c = getchar();
		while(c > '9' || c < '0') s |= c == '-', c = getchar();
		while(c >= '0' && c <= '9') o = o * 10 + c - '0', c = getchar();
		if(s) o = -o;
	}
} using fastIO::read;
typedef long long ll;
#define eb emplace_back
template<typename T> inline void cmin(T &a, T b) {
	if(a > b) a = b;
}
const int N = 2e5 + 5;
int n, m, k;
ll v[N], v2[N];
namespace A {
	vector<int> g[N];
	int dfn[N], low[N], ins[N], in[N], cnt, dfc;
	stack<int> stk;
	vector<int> scc[N];
	void tarjan(int u) {
		dfn[u] = low[u] = ++dfc, stk.push(u), ins[u] = true;
		for(int v : g[u]) {
			if(!dfn[v]) tarjan(v), cmin(low[u], low[v]);
			else if(ins[v]) cmin(low[u], dfn[v]);
		}
		if(low[u] == dfn[u]) {
			++cnt;
			for(int x = stk.top(); stk.size(); x = stk.top()) {
				in[x] = cnt, scc[cnt].eb(x);
				stk.pop(), ins[x] = false;
				if(x == u) break;
			}
		}
	}
}
// 最大路径长与最大流，含双倍点和超级源汇的总点数 
const int MAXF = 1e9, N2 = N * 2, E = N2 * 8;
const ll MAXC = LLONG_MAX / 2;
struct MCMF {
	int n, s, t, maxf;
	struct edge {
		int v, f, nxt;
		ll c;
	} e[E];
	int hd[N2], ind[N2], vis[N2], cnt = 1;
	ll minc, h[N2], dis[N2];
	void eadd(int u, int v, int f, ll c) {
		e[++cnt].v = v, e[cnt].f = f, e[cnt].c = c;
		e[cnt].nxt = hd[u], hd[u] = cnt;
		e[++cnt].v = u, e[cnt].f = 0, e[cnt].c = -c;
		e[cnt].nxt = hd[v], hd[v] = cnt;
		++ind[v];
	}
	void toposort() {
		queue<int> q;
		for(int i = 1; i <= n; i++) {
			h[i] = MAXC;
			if(!ind[i]) q.push(i);
		}
		h[s] = 0;
		while(!q.empty()) {
			int u = q.front();
			q.pop();
			for(int i = hd[u]; i; i = e[i].nxt) {
				if(!e[i].f) continue; // 不可以走反边！ 
				int v = e[i].v;
				cmin(h[v], h[u] + e[i].c);
				if(--ind[v] == 0) q.push(v);
			}
		}
	}
	struct node {
		ll dis;
		int id;
		bool operator<(const node &a) const {
			return dis > a.dis;
		}
	};
	struct path {
		int v, e;
	} p[N2];
	bool dijkstra() {
		priority_queue<node> q;
		for(int i = 1; i <= n; i++) dis[i] = MAXC, vis[i] = false;
		dis[s] = 0, q.push(node{0, s});
		while(!q.empty()) {
			int u = q.top().id;
			q.pop();
			if(vis[u]) continue;
			vis[u] = true;
			for(int i = hd[u]; i; i = e[i].nxt) {
				int v = e[i].v;
				ll nc = e[i].c + h[u] - h[v];
				if(e[i].f && dis[v] > dis[u] + nc) {
					dis[v] = dis[u] + nc;
					p[v].v = u, p[v].e = i;
					if(!vis[v]) q.push(node{dis[v], v});
				}
			}
		}
		return dis[t] != MAXC;
	}
	pair<int, long long> solve() {
		toposort();
		while(dijkstra()) {
			int minf = MAXF;
			for(int i = 1; i <= n; i++) h[i] += dis[i];
			for(int i = t; i != s; i = p[i].v) cmin(minf, e[p[i].e].f);
			for(int i = t; i != s; i = p[i].v) {
				e[p[i].e].f -= minf, e[p[i].e ^ 1].f += minf;
			}
			maxf += minf, minc += minf * h[t];
		}
		return make_pair(maxf, minc);
	}
} net;

int main() {
	read(n), read(m), read(k);
	for(int i = 1, u, v; i <= m; i++) {
		read(u), read(v);
		A::g[u].eb(v);
	}
	for(int i = 1; i <= n; i++) read(v[i]);
	for(int i = 1; i <= n; i++)
		if(!A::dfn[i]) A::tarjan(i);
	net.n = A::cnt * 2;
	net.s = A::in[1], net.t = ++net.n;
	for(int i = 1; i <= A::cnt; i++) {
		for(int x : A::scc[i]) {
			v2[i] += v[x];
			for(int y : A::g[x]) {
				if(A::in[x] != A::in[y]) 
					net.eadd(i + A::cnt, A::in[y], k, 0); 
					// 可能会建出重边，但没有关系，在汇点处设置一个流量限制即可 
			}
		}
		net.eadd(i, i + A::cnt, 1, -v2[i]);
		net.eadd(i, i + A::cnt, k, 0);
		net.eadd(i + A::cnt, net.t, k, 0);
	}
	net.eadd(net.t, net.t + 1, k, 0);
	net.t = ++net.n;
	cout << -net.solve().second << '\n';

	return 0;
}

坑

tarjan 用 dfn[v] 更新 low[u]，v必须在搜索树内(ins[v])
用拓扑排序处理第一次最短路不能走反向边，不然会出现负环
拓扑排序不能只把原点放进初始队列，有些原点到不了的点入度也可能为 0
即使边权都是负的，但因为反向边的存在，MAXC 也得设置为 N * X_i!!!
可能全部被缩成一个点，加边时的 c 也要设置为 long long

这种题漏开 long long 真的会烦死。建议 #define int long long 用于检测是否漏开。

posted @ 2022-04-12 15:00 huaruoji 阅读(227) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 【笔记】分层图DJ

· 【笔记】常数研究

· 网络流学习笔记

· 网络流小记

· 网络流初步

阅读排行：
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· 单线程的Redis速度为什么快？
· 展开说说关于C#中ORM框架的用法！
· Pantheons：用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探

滑蒻稽的博客

Huaruoji