CSP-S 2019 解题报告(格雷码)

T1 格雷码

首先看到这是一道普及-的题,我深表惊讶.于是决定认真想一想来测试一下我的智商是否达到了OIer准入水平,于是,我被自己的智慧所折服了~（来自 2022 年的批注：你就是个傻呗）

---

阅读题目我们可以发现生成的格雷码是一个长度为$2^n$的数列,既然放在第一题就一定有各种奇葩的简单做法,找规律又有何不可呢?(实际上,其他题解也有大佬是直接按照题意模拟的,这算是正向思维.根据生成的数列找到规律算是一种逆向思维啦)

题目中给出的$n=3$的情况对我来说还不便于寻找规律,我们把$n=4$的表列出来:
$$0000,0001,0011,0010,0110,0111,0101,0100,1100,1101,1111,1110,1010,1011,1001,1000$$
显然,每一位是$0$或$1$都是有规律的,考虑到生成算法是分成了2部分进行,我们可以画出一颗二叉树(我也不知道我怎么想到的):

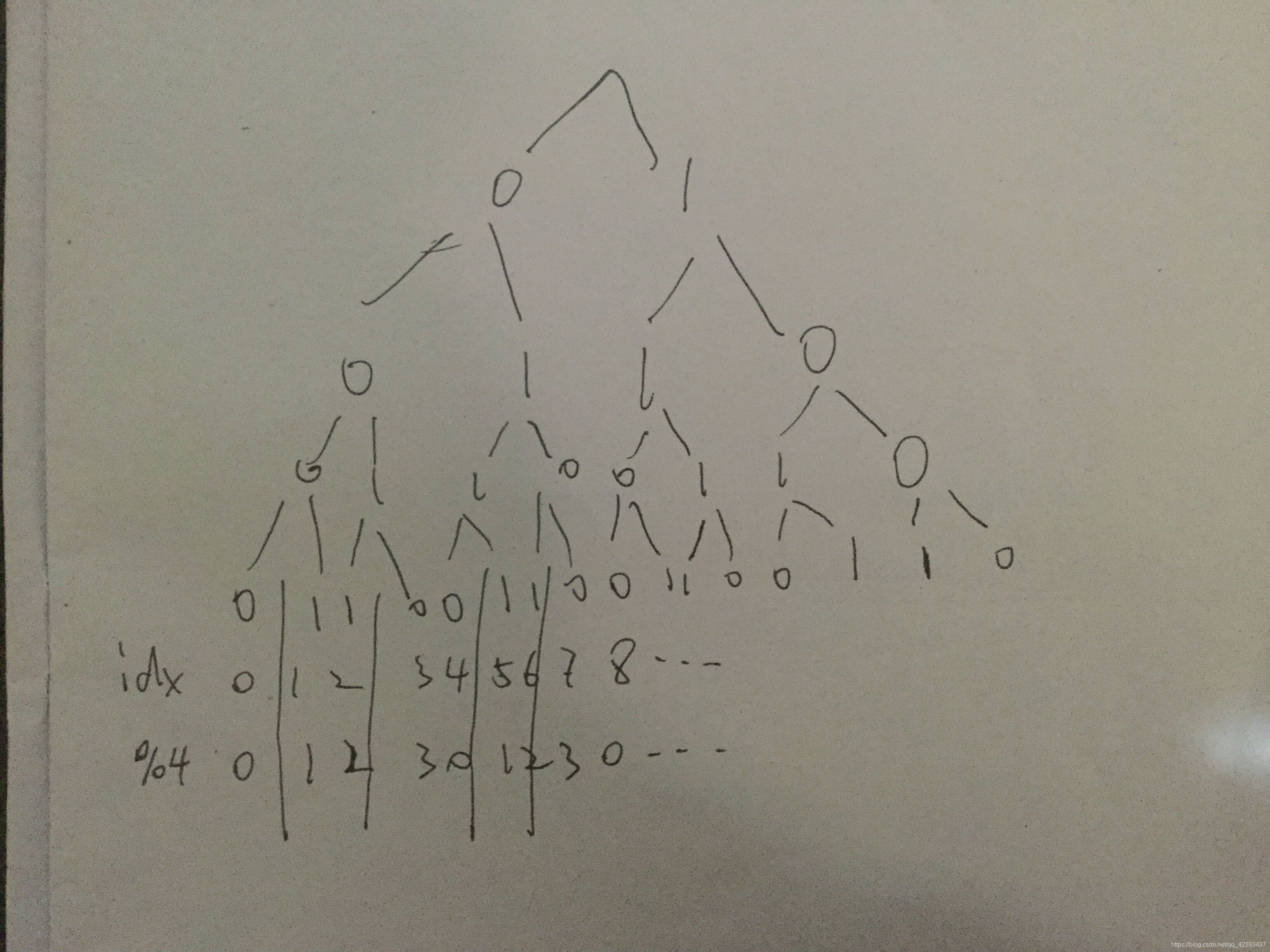
从最下一层序号位置向上遍历,就可得到整个格雷码.

回到孩子的操作为$idx÷2$,求得当前值为0或1的算法是:
$$an{s}^p=\{\begin{array}{ll}1& idx\mathrm{m}\mathrm{o}\mathrm{d}4==1or2\\ 0& idx\mathrm{m}\mathrm{o}\mathrm{d}4==0or3\end{array}$$
代码:

#include <bits/stdc++.h>

using namespace std;
unsigned long long k;
int ans[70],n,p;

int main()
{
	cin>>n>>k;
	p=n;
	while(p--)
	{
		int modx=k%4;
		if(modx==1||modx==2) ans[p]=1;
		else ans[p]=0;
		k/=2;
	}
	for(int i=0;i<n;i++)
	{
		cout<<ans[i];
	}
	
	return 0;
}