初级图论1

图论很重要

 

题目：https://vjudge.net/contest/198762#problem/A

A - 昂贵的聘礼

       年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说："嗯，如果你能够替我弄到大祭司的皮袄，我可以只要8000金币。如果你能够弄来他的水晶球，那么只要5000金币就行了。"探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。
为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。每个物品都有对应的价格P，主人的地位等级L，以及一系列的替代品Ti和该替代品所对应的"优惠"Vi。如果两人地位等级差距超过了M，就不能"间接交易"。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。

Input

输入第一行是两个整数M，N（1 <= N <= 100），依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X（X < N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和"优惠价格"。

Output

输出最少需要的金币数。

Sample Input

1 4
10000 3 2
2 8000
3 5000
1000 2 1
4 200
3000 2 1
4 200
50 2 0

Sample Output

5250

题目意思：

    按例子讲：
输入1和4    分别是1个等级差距限制和4个物品（相当与主人数），

输入 10000 3 2分别是    10000的价值的物品    3的主人等级   主人提出的两个物品兑换

输入 2 8000      分别是      2号物品（主人）  +   8000金币数 才能兑换

输入 3 5000    同上

输入1000  2  1   分别是     1000的价值的物品    2的主人等级   主人提出的两个物品兑换

。。。。。。。

5250的得出      从第一个主人开始 ： 兑换3号物品+5000  

                        然后 从3号主人开始 ： 兑换4号物品+200

                         再然后从4号主人开始 ：没有兑换的物品只能付50金币买物品

           所付金币就为   5000+200+50=5250

题解：

 

 

 

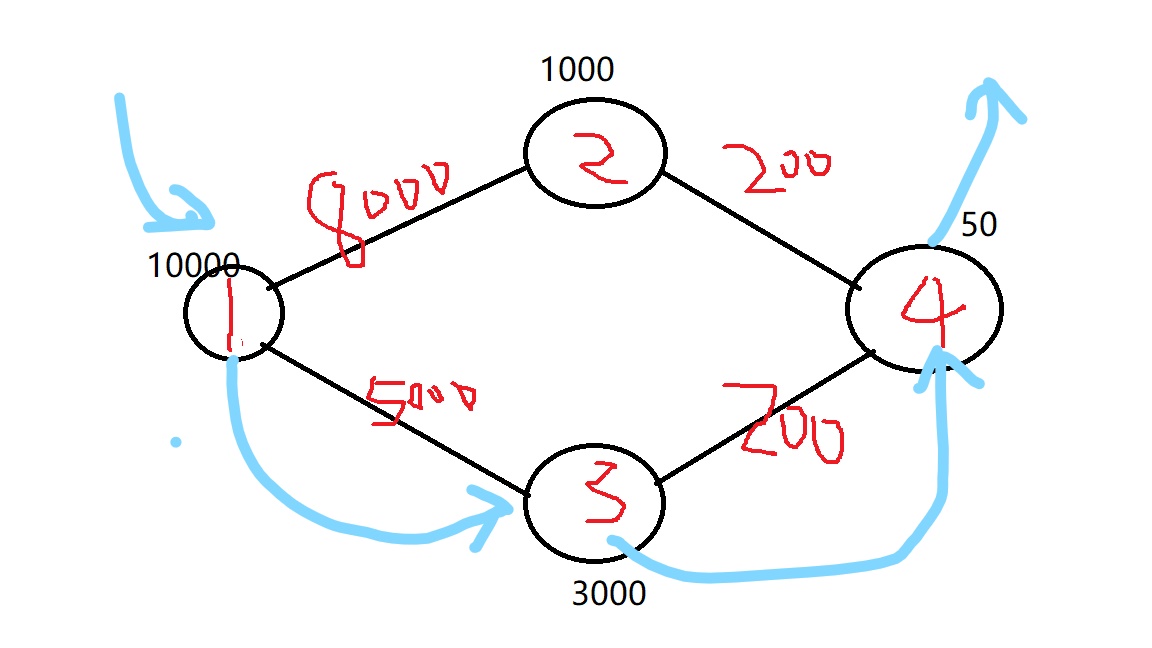
dijkstra（迪杰斯特拉）算法遍历图求最短路+等级制度的处理

dijkstra（迪杰斯特拉）算法：https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html（里面动态图挺容易懂的）

AC代码：（网上抄的）

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;

#define INF 0x3f3f3f3f
int mp[1100][1100];
int gg[11000];
int vis[11000];
int dis[11000];
int m,n;

int dijkstra()
{
int i,j;
memset(dis,0,sizeof(dis));
for(i=1; i<=n; i++)//将从每一个点出发所需要的金币看做0到该点所需要的金币数目
dis[i]=mp[0][i];
for(i=1; i<n; i++)
{
int mina=INF;
int u,k;
for(j=1; j<=n; j++)
{
if(!vis[j] && dis[j]<mina)
{
mina=dis[j];
u=j;
}
}
vis[u]=1;
for(k=1; k<=n; k++)
{
if(!vis[k] && mp[u][k]<INF && dis[k]>dis[u]+mp[u][k])
dis[k]=dis[u]+mp[u][k];
}
}
return dis[1];//返回每一个点到酋长处所花费的钱数
}

int main()
{
while(~scanf("%d%d",&m,&n))
{
int i,j,a,b,c,e,r;
for(i=0; i<=n; i++)//初始胡为不能相通
for(j=0; j<=n; j++)
mp[i][j]=INF;
for(i=1; i<=n; i++)
{
scanf("%d%d%d",&a,&b,&c);
mp[0][i]=a;//将从每一个点出发所需要的金币看做0到该点所需要的金币数目
gg[i]=b;
for(j=1; j<=c; j++)
{
scanf("%d%d",&e,&r);
mp[e][i]=r;//单向路径，且等级e低于i，低等级通向高等级
}
}
int minn=INF;
for(i=1; i<=n; i++)//枚举每一个人为最低等级
{
int mnn=gg[i];
memset(vis,0,sizeof(vis));//注意初始化
for(j=1; j<=n; j++)//标记等级差距过大，和等级低于自己的人
{
if(gg[j]<mnn || gg[j]-mnn>m)
vis[j]=1;
else
vis[j]=0;
}
int ss=dijkstra();
minn=min(minn,ss);
}
printf("%d\n",minn);
}
return 0;
}