线性拟合-实验报告
一.实验方法:
1最小二乘法
2梯度下降法
二.公式推导
1 最小二乘
用线性函数h a(x)=a0+a1*x来拟合y=f(x);
构造代价函数J(a):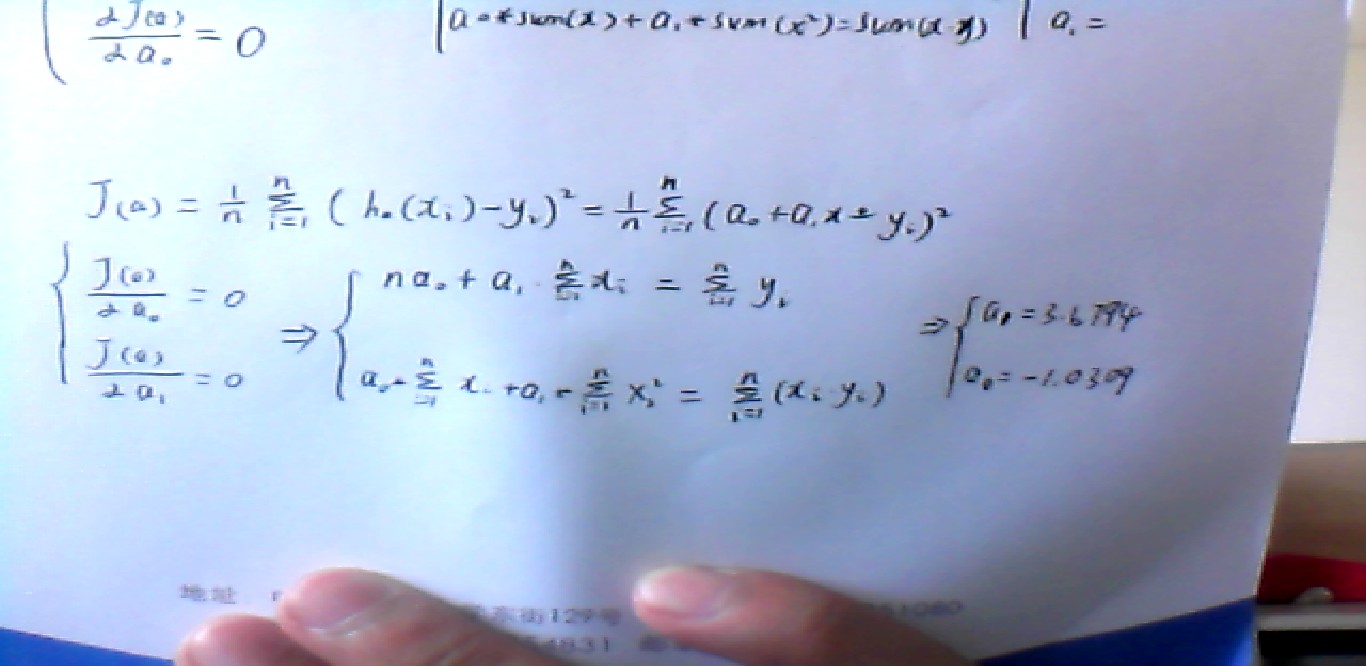
代价函数分别对a0和a1求偏导,连个偏导数都等于0成为两个方程,两个方程联合求解得到a0和a1;
2 梯度下降
构造代价函数J(a),J(a)对a0,a1分别求偏导得到梯度,
〆J(a)/〆a0=n*a0+a1*sumx-sumy;
〆J(a)/〆a1=a1*sumx*sumx+a0*sumx-sumx*sumy;
tidu_a0=n*a0+a1*sumx-sumy;
tidu_a1=a1*sumxx+a0*sumx-sumxy;
设置步长为l,迭代m次
delta_r=sqrt(tidu_a0*tidu_a0+tidu_a1*tidu_a1);
a0=a0-l*(tidu_a0/tidu_r);
a1=a1-l*(tidu_a1/tidu_r);
每次迭代显示得到的直线和mse,并修订学习率
%显示直线
x2=[-0.1,1.1];
y2=x2.*a1+a0;
plot(x2,y2,'color',[1-i/m,1-i/m,1-i/m]);
%显示错误
error=0;
for j=1:n
error=error+(y(j)-(a1*x(j)+a0))*(y(j)-(a1*x(j)+a0));
end
mse=error/n;
l=mse;
mse
三.matlab代码
1 最小二乘法代码:
%in是一个100行2列的矩阵,两列分别为x和y。用一条直线y=x*a+b拟合x和y的关系;
%用最小二乘法计算a和b。
x=in(1:100,1);y=in(1:100,2);sumx=0;sumy=0;sumxx=0;sumyy=0;sumxy=0;for i=1:1:100 sumx=sumx+x(i); sumy=sumy+y(i); sumxx=sumxx+x(i)*x(i); sumyy=sumyy+y(i)*y(i); sumxy=sumxy+x(i)*y(i);endplot(in(:,1),in(:,2),'r.'); %用红色的点画出100个样本点hold on; %保留当前绘图,不被下次绘图遮盖n=100;[b,a]=solve('n*a0+a1*sumx=sumy','a0*sumx+a1*sumxx=sumxy','a0','a1');
%解二元一次方程组,未知数为a0,a1,结果返回给b和a。a=eval(a);
%eval(str),把str当做一条语句执行b=eval(b);x2=[0,1];
%知道解析式y=a*x+b,画直线的方法y2=x2.*a+b;
% 因为x2是一个向量,所以用x2.表示plot(x2,y2);
%制动化一条以x2为x,以y2为y的直线 mse=0;error=0;for i=1:n error=error+(y(i)-(a*x(i)+b))*(y(i)-(a*x(i)+b));endmse=error/n;mse
2 梯度下降法代码:
x=in(1:100,1);
y=in(1:100,2);
sumx=0;
sumy=0;
sumxx=0;
sumyy=0;
sumxy=0;
for i=1:1:100
sumx=sumx+x(i);
sumy=sumy+y(i);
sumxx=sumxx+x(i)*x(i);
sumyy=sumyy+y(i)*y(i);
sumxy=sumxy+x(i)*y(i);
end
plot(in(:,1),in(:,2),'r.');
hold on;
a0=2;
a1=1;
l=0.5;
n=100;
m=50;
for i=0:1:m
tidu_a0=n*a0+a1*sumx-sumy;
tidu_a1=a1*sumxx+a0*sumx-sumxy;
tidu_r=sqrt(tidu_a0*tidu_a0+tidu_a1*tidu_a1);
a0=a0-l*(tidu_a0/tidu_r);
a1=a1-l*(tidu_a1/tidu_r);
x2=[-0.1,1.1];
y2=x2.*a1+a0;
plot(x2,y2,'color',[1-i/m,1-i/m,1-i/m]);
error=0;
for j=1:n
error=error+(y(j)-(a1*x(j)+a0))*(y(j)-(a1*x(j)+a0));
end
mse=error/n;
l=mse;
mse
end
四.运行结果
1 最小二乘法结果:
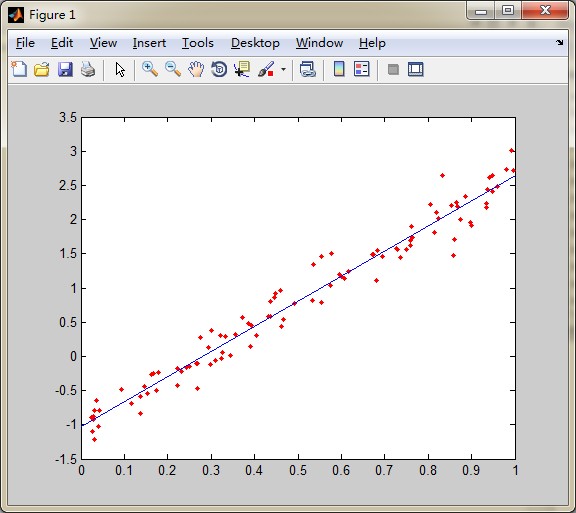
2梯度下降法结果
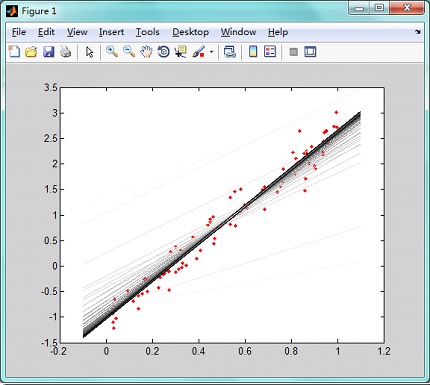
五.误差
1 最小二乘法
A1=3.679365985769617
A0=--1.030876273676726
均方误差mse=0.0429
2梯度下降法
(起点为a0=2,a1=1;迭代次数为50次)
A1=3.67860477725630
A0=-1.00565713447357
均方误差mse =0.0436
使用mesh查看损失函数与a0,a1的关系:
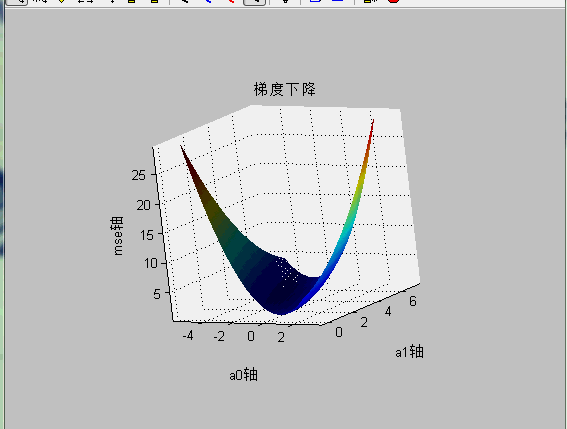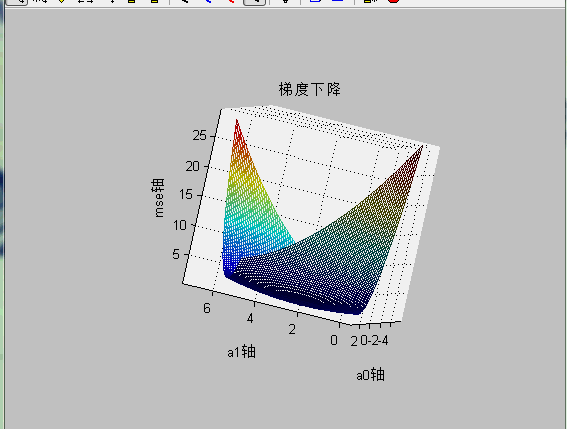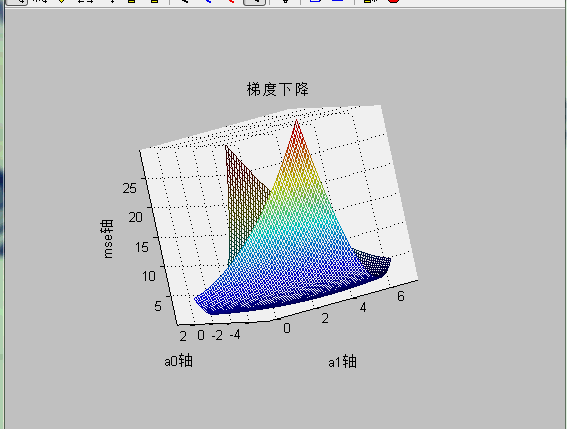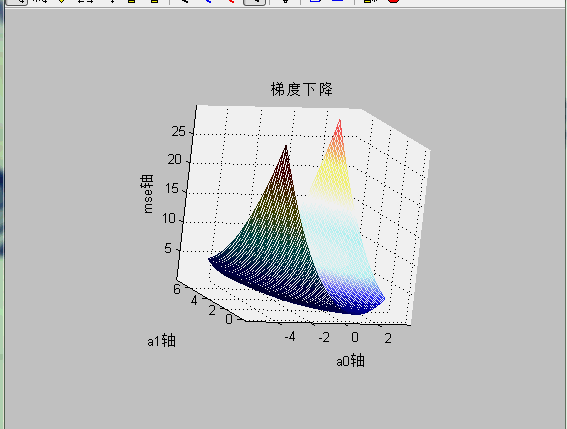
mesh显示mse的代码:
x=in(1:100,1);
y=in(1:100,2);
sumx=0;
sumy=0;
sumxx=0;
sumyy=0;
sumxy=0;
for i=1:1:100
sumx=sumx+x(i);
sumy=sumy+y(i);
sumxx=sumxx+x(i)*x(i);
sumyy=sumyy+y(i)*y(i);
sumxy=sumxy+x(i)*y(i);
end
n=100;
a0=-4.5:0.1:2.5;
a1=0:0.1:7;
[A0,A1]=meshgrid(a0,a1);
Z=(sumyy+A0.*A0.*n+A1.*A1.*sumxx+A0.*A1.*2*sumx-A0.*2*sumy-A1.*2*sumxy)/n;
mesh(A0,A1,Z);
xlabel('a0轴');
ylabel('a1轴');
zlabel('mse轴');
title('梯度下降');
六.附数据 in.txt
0.9005 1.9113
0.4480 0.9218
0.2689 -0.4654
0.5538 1.4667
0.1788 -0.2393
0.8597 1.7048
0.2320 -0.2135
0.1681 -0.2549
0.0267 -1.0928
0.3224 0.2985
0.5552 0.7931
0.8245 2.0172
0.8042 2.2273
0.0244 -0.8888
0.3715 0.5687
0.4919 0.7795
0.4661 0.5348
0.0417 -0.7969
0.6170 1.2403
0.5780 1.5113
0.2988 -0.1120
0.4357 0.5782
0.1366 -0.8407
0.2997 0.3807
0.7614 1.8959
0.0353 -0.6399
0.2695 -0.1072
0.9963 2.7233
0.4469 0.8604
0.1528 -0.5472
0.8862 2.3398
0.0314 -1.2190
0.1160 -0.6832
0.2509 -0.1495
0.7597 1.6176
0.8983 1.9552
0.2234 -0.1696
0.6733 1.4859
0.8188 2.1008
0.9489 2.6517
0.8743 2.0069
0.3937 0.4557
0.9370 2.4427
0.4369 0.8025
0.1625 -0.2676
0.3098 -0.0641
0.6811 1.1038
0.9341 2.2406
0.9474 2.6501
0.5991 1.1617
0.9489 2.4170
0.4040 0.3019
0.0410 -1.0271
0.2938 0.1261
0.0319 -0.7842
0.8645 2.2468
0.4325 0.5829
0.0928 -0.4767
0.1378 -0.5801
0.2420 -0.1617
0.2230 -0.4245
0.8677 2.1976
0.7642 1.7447
0.3447 0.0178
0.3848 0.4811
0.5949 1.2016
0.5351 1.3388
0.3336 0.2838
0.8547 2.2127
0.2656 -0.1061
0.9339 2.1840
0.3898 0.1515
0.6831 1.5417
0.2750 0.2706
0.0280 -0.8750
0.9406 2.6179
0.5340 0.8242
0.6712 1.4927
0.6075 1.1417
0.7509 1.5665
0.9813 2.7267
0.7277 1.5830
0.8573 1.4756
0.9918 3.0038
0.7595 1.6970
0.1460 -0.4369
0.3263 0.0628
0.0288 -0.9162
0.6946 1.4643
0.9588 2.4821
0.7290 1.5572
0.7368 1.4520
0.1746 -0.4995
0.3554 0.3202
0.5746 1.0338
0.4599 0.9678
0.8337 2.6507
0.8154 1.8128
0.3240 -0.0295
0.4617 0.4441



