2018.07.17【省赛模拟】模拟B组 比赛总结
题目
【GDKOI2003】最大公共子串
【题目描述】
从一个给定的串中删去(不一定连续地删去)0个或0个以上的字符,剩下的字符按原来的顺序组成的串是该串的字串。例如:“”, “a”, “aaa”,“bbb”,“xabb”,“xaaabbb”都是串“xaaabbb”的字串。(例子中的串不包括引号)
编程求N个非空串的最长公共子串的长度。
限制:2<=N<=100:N个串中的字符只会是数字0,1,…,9或小写字母a,b,…,z;每个串非空且最多含100个字符;N个串的长度的乘积不会超过30000。
【输入】
文件第一行是一个整数T,表示测试数据的个数(1<=T<=10)。接下来T组测试数据。各族测试数据的第一行是一个整数Ni,表示第i数据中串的个数。各组测试数据的第2到N+1行中,每行一个串,串中不会有空格,但行首和行未可能有空格,这些空格当然不算作串的一部分。
【输出】
输出T行,每行一个数,第I行的数表示第I组测试数据中Ni的非空串的最长公共子串的长度
【样例输入】
1
3
ab
bc
cd
【样例输入】
0
【GDKOI2003】分球
【题目描述】
在一个装满财宝的屋子里,有2N个盒子排成一排。除了两个相邻的空盒外,其余的每个盒子里都装有一个金球或者一个银球,总共有N-1个金球和N-1个银球。以下是一个N=5时的例子,G表示金球,S表示银球:

任意两个相邻的非空的盒子里的球可以移动到两个相邻的空盒中,移动不能改变这两个球的排列顺序。写一个程序,用最少的移动次数把所有的金球都移到所有银球的左边。
【输入】
输入文件包含多组数据。第一行为K,表示数据的总数。
每组数据的第一行是N(3<=N<=7),第二行是2N个盒子的初始状态。金球用a表示,银球用b表示,空盒用空格表示。每两组相邻数据用空行隔开。
【输出】
对于每一组数据,若无解则输出一行-1,若有解,输出最少移动次数,相邻的两组数据用一个空行隔开。
【输入】
3
3
abab
5
abba abab
6
a babbababa
【输出】
-1
3
4
【数据范围限制】
k<5
【GDKOI2004】使命的召唤
【题目描述】
你玩过call of duty这个游戏吗?这个游戏以诺曼底登陆为背景,假设你是盟军的一员,身在前线去完成许多任务而粉碎纳粹的野心。现在假设有一个任务,德军有很多机枪阵地,火力很猛,如果不把它们摧毁就会对盟军的推进造成很大损失,盟军打算派出一些敢死队员深入阵地把这些机枪阵地炸毁,当然,敢死队员会有很大的生命危险,所以盟军的指挥官希望你能帮他把损失降到最少。
【输入】
输入数据第一行是一个整数n(1<=n<=200),代表有多少个机枪阵地需要摧毁。然后接下来n行,每行两个整数xi,yi,代表每个机枪阵地的坐标(0<=xi,yi<=30000),然后接着一个整数m,跟着有m行,每行两个整数p和q(1<=p,q<=n,p<>q),代表机枪阵地p和机枪阵地q之间有路相连,敢死队员炸掉一个机枪阵地之后,必须从当前的机枪阵地出发沿着路到达下一个x坐标比当前阵地大的阵地(因为机枪阵地的纵深方向是沿着x坐标递增方向的),如果不存在这样的阵地,那这名敢死队员就完成任务了。简单来说,一个敢死队员可以空降到任意一个机枪阵地(设为a0),然后从这个阵地出发按照上面所述可以摧毁一系列机枪阵地(顺序列为a0,a1,a2...ak),而这一系列机枪阵地的x坐标满足(x0 < x1 < x2 < ... < xk)。从安全和效率出发,每个敢死队员可以带任意个炸弹。任意两个敢死队员的路线不能有交点。现在问你怎么安排敢死队员的路线,可以使到用最小数目的敢死队员去完成这个艰巨的任务。
【输出】
输出一个整数,就是所求的敢死队员的最小数目。
【样例输入】
4
25990 5850
8263 2957
1067 22231
4109 4577
3
4 1
2 4
1 3
【样例输出】
2
【样例解释】
上面的例子最少需2个敢死队员,1种方案是:1个摧毁阵地4后再去摧毁阵地2,1个敢死队员摧毁阵地3后去摧毁阵地1。
【数据范围限制】
m<10000
过程
这次比赛似乎没有那么难了(某一次比赛,三道题的算法都是我没有学过的毒瘤算法)
第一题
比赛时没有看出是什么东东,发现它可以随便地删除字符,但暴搜明显爆炸(串的长度最长有100)。想到hash,但不知道怎么搞,于是果断放弃。
第二题
这题看起来很可做,但无论我怎么模拟样例都过不了。
自尊心大大受创,遂弃疗。
后来想完第三题,我又折回来做第二题,发现可以用双向BFS+哈希暴力做。
于是便打起了代码,但最后只拿到了87.5分。
第三题
这题看上去很像一道二分图最大匹配。但是看到“任意两个敢死队员的路线不能有交点”时,我懵逼了——这不是计算几何吗?!怎么算两条线段间有没有交点啊?!我不会呀!
但我不愿放弃,于是又想了一会儿。。。
发现题目没有说敢死队员要怎么走,也就是说两条路径相交时,敢死队员会绕开:
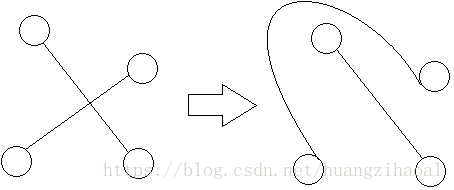
这样似乎就解决了问题,但是我却没有在题目里面发现这样的字样,遂弃疗。
后来打了个表,12.5分。
总分
0+87.5+12.5=100
题解
T1
方法一:DP(正解)
设\(f_{x_1,x_2,x_3,...,x_n}\)表示第1个字符串在前\(x_1\)个字符中取子串,第2个字符串在前\(x_2\)个字符中取子串……第i个字符串在前\(x_i\)个字符中取子串。
那么就可以列出状态转移方程:
但是这样DP,数组要开到\(10^{200}\)那么大,明显爆炸。
这时我们就要用另一种开数组的方法了。
再看一下题目,发现了这句话:“N个串的长度的乘积不会超过30000”
因此,我们只用开DP数组\(f[0..30000]\),其中原来\(f_{x_1,x_2,x_3,...,x_n}\)的指改为储存在\(f_{(x_1-1)+(x_2-1)*|S_1|+(x_3-1)*|S_1|*|S_2|+...+(x_n-1)*|S_1|*|S_2|*...*|S_{n-1}\space|}\)中。
这里可以用dfs实现。
方法二:分类讨论(水法)
其实我们完全可以在最短串中暴力搞出一个子串,然后逐个串判断。
其中(设S为极限情况下的输入的最短串)
①当\(n=1\)时
\(|S|=30000\)
这样枚举明显爆炸。
但是这时的答案明显为\(|S|\),直接输出即可。
②当\(n=2\)时
\(|S|\approx \sqrt{30000}\approx 173\)
这样还是会炸。
这时,我们可以弄一个2维DP,搞一搞就可以了。
③当\(n=3\)时
\(|S|\approx \sqrt[3]{30000}\approx 31\)
似乎会炸,于是再搞一个3维DP。
④当\(n=4\)时
\(|S|\approx \sqrt[4]{30000}\approx 13\)
这时就不会再炸了。因此当\(n\geq 4\)时可以直接用暴力做。
方法三:hash
实话说这方法麻烦得很,我也不太会,这里就不加阐述了。
据说此题还可以用后缀自动机?!
T2
这题明显是暴搜,但我担心时间会炸,于是打了个双向BFS。
起点的初始状态就是输入的那个,而终点的状态就是所有金球在左,银球在右的状态(枚举空格)。
可以设空格为0,金球为1,银球为2,压一下状态,然后用哈希判重。
这里的哈希值取得要好,既要是状态总数的2~3倍,也要不那么大(以免爆空间)。由于空间开得挺大的(128000KB),因此我用了11454637。
这题应该是所有题目中最水的,然而我比赛时却只拿了87.5分。
后来找了半天,发现是读入出了问题:
我本想用scanf("\n");把回车给弄掉,结果却莫名其妙地把行首空格也处理掉了。后来改用getchar();就对了。
注意:这题输出时行与行之间不要有空行,不然会WA
T3
这题果然是二分图最大匹配,和我想的一模一样(敢死队员可以绕过去)。
看来想问题有事不能想太多呀!
因为队员们的路线不能有交点,又要走到每一个机枪阵地,因此我们可以推断出一个结论:每一个机枪阵地最多只能从一个机枪阵地走过来。因此我们只要计算最少有多少个机枪阵地不可以从别的机枪阵地走来就可以了。
我们可以新建一个源点S,从它连接n条边到n个机枪阵地。再把所有的机枪阵地克隆一份到右边(第i个点克隆后成为第i+n个点),若是能从阵地x走到阵地y,那么就在点x和点y+n间连一条边。最后在从所有的右边的点连边到汇点T。
其中,所有的边的流量都为1。
当然,这题也可以用匈牙利算法来做。
最后输出n-最大匹配数即可。
标程
T1
#include<cstdio>
#include<cstring>
using namespace std;
#define M 30005
#define N 105
int n,len[N],f[M],x[N];
char s[N][N];
inline int max(int x,int y){return x>y?x:y;}
int dp()
{
int i,j,index=x[n]-1;
if(x[n]==0) return 0;
for(i=n-1;i>0;i--)
{
if(x[i]==0) return 0;
index=index*len[i]+x[i]-1;
}
if(f[index]>=0) return f[index];
for(i=2;i<=n;i++)
{
if(s[1][x[1]]!=s[i][x[i]])
{
for(j=1;j<=n;j++)
{
x[j]--;
f[index]=max(f[index],dp());
x[j]++;
}
return f[index];
}
}
for(i=1;i<=n;i++) x[i]--;
j=dp()+1;
for(i=1;i<=n;i++) x[i]++;
return f[index]=j;
}
int main()
{
int tt,i,j;
scanf("%d",&tt);
while(tt--)
{
memset(f,-1,sizeof(f));
scanf("%d\n",&n);
for(i=1;i<=n;i++)
{
scanf("%s",s[i]+1);
x[i]=len[i]=strlen(s[i]+1);
}
printf("%d\n",dp());
}
return 0;
}
T2
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
#define mod 11454637
struct node
{
int now,step;
};
int hasha[mod+10],hashb[mod+10],input[20],n,step;
queue<node>a;
queue<node>b;
void swap(int &x,int &y){int z=x;x=y;y=z;}
bool finda(int k,bool b)
{
int x=k%mod+1;
while(hasha[x]&&hasha[x]!=k) x=(x+1)%mod+1;
if(hasha[x]==k) return 1;
if(b) hasha[x]=k;
return 0;
}
bool findb(int k,bool b)
{
int x=k%mod+1;
while(hashb[x]&&hashb[x]!=k) x=(x+1)%mod+1;
if(hashb[x]==k) return 1;
if(b) hashb[x]=k;
return 0;
}
int bfsa()
{
node u;int i,j,k,t,num[20];
while((!a.empty())&&(a.front()).step==step)
{
u=a.front();a.pop();
k=u.now,i=j=0;
while(i<n)
{
num[++i]=k%3;
if(num[i]==0&&j==0) j=i;
k/=3;
}
for(i=1;i<n;i++) if(i!=j&&i!=j-1&&i!=j+1)
{
swap(num[i],num[j]);
swap(num[i+1],num[j+1]);
for(k=n,t=0;k>0;k--) t=t*3+num[k];
if(!finda(t,1))
{
if(findb(t,0)) return step*2+1;
a.push((node){t,step+1});
}
swap(num[i],num[j]);
swap(num[i+1],num[j+1]);
}
}
return 0;
}
int bfsb()
{
node u;int i,j,k,t,num[20];
while((!b.empty())&&(b.front()).step==step)
{
u=b.front();b.pop();
k=u.now,i=j=0;
while(i<n)
{
num[++i]=k%3;
if(num[i]==0&&j==0) j=i;
k/=3;
}
for(i=1;i<n;i++) if(i!=j&&i!=j-1&&i!=j+1)
{
swap(num[i],num[j]);
swap(num[i+1],num[j+1]);
for(k=n,t=0;k>0;k--) t=t*3+num[k];
if(!findb(t,1))
{
if(finda(t,0)) return step*2+2;
b.push((node){t,step+1});
}
swap(num[i],num[j]);
swap(num[i+1],num[j+1]);
}
}
return 0;
}
int main()
{
int tt,i,j,k,t;char ch;
bool bk;
scanf("%d\n",&tt);
while(tt--)
{
memset(hasha,0,sizeof(hasha));
memset(hashb,0,sizeof(hashb));
while(!a.empty()) a.pop();
while(!b.empty()) b.pop();
scanf("%d",&n);i=k=step=0;
getchar();
while(ch=getchar(),ch==' '||ch=='a'||ch=='b')
{
if(ch==' ') input[++i]=0;
else input[++i]=ch-'a'+1;
}
n<<=1;
for(j=n;j>0;j--) k=k*3+input[j];
i=finda(k,1);
a.push((node){k,0});
bk=0;
for(i=1;i<n;i++)
{
k=t=0;
for(j=n;j>0;j--)
{
if(j!=i&&j!=i+1)
{
t++;
if(t<n/2) k=k*3+2;
else k=k*3+1;
}
else k*=3;
}
t=findb(k,1);
b.push((node){k,0});
if(finda(k,0)) bk=1;
}
if(bk) puts("0");
else
{
while((!a.empty())&&(!b.empty()))
{
i=bfsa();
if(i>0) break;
i=bfsb();
if(i>0) break;
step++;
}
if(i>0) printf("%d",i);
else printf("-1");
if(tt>0) printf("\n");
}
}
return 0;
}
T3
#include<cstdio>
using namespace std;
#define M 40405
#define N 405
#define S 401
#define T 402
struct edge
{
int start,end,lenth,next;
}a[M];
int x[N],first[N],dis[N],GAP[N],n,s=1;
inline int mymin(int x,int y){return x<y?x:y;}
void inc(int x,int y)
{
a[++s]=(edge){x,y,1,first[x]};
first[x]=s;
a[++s]=(edge){y,x,0,first[y]};
first[y]=s;
}
int sap(int k,int flow)
{
if(k==T) return flow;
int have=0,i,now;
for(i=first[k];i;i=a[i].next)
{
if(dis[a[i].start]==dis[a[i].end]+1&&a[i].lenth)
{
now=sap(a[i].end,mymin(a[i].lenth,flow-have));
a[i].lenth-=now,a[i^1].lenth+=now,have+=now;
if(flow==have) return have;
}
}
if((--GAP[dis[k]])==0) dis[S]=n;
++GAP[++dis[k]];
return have;
}
int main()
{
int m,i,j,u,v,ans=0;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d%d",&x[i],&j);
inc(S,i),inc(i+n,T);
}
scanf("%d",&m);
for(i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
if(x[v]>x[u]) inc(u,v+n);
if(x[u]>x[v]) inc(v,u+n);
}
while(dis[S]<n) ans+=sap(S,N);
printf("%d\n",n-ans);
return 0;
}


