筷子
【题目描述】
一个怪人,吃东西时使用三根筷子,二短一长,设它们的长为A≤B≤C。并定义它的"坏度"为(A - B)^2。这一天,他要请K个客人来家里吃饭,另外他自己家里还有8个人,因而要准备K+8套这种特别的筷子。但发现家里的筷子全是不一样长的。
请你将这些筷子分成K+8套,要求总的"坏度"值最小。
【输入】
第一行一个整数T,表示测试数据的组数,每组测试数据输入共2行:
第1行两个整数K和N,分别表示要请K个客人来家里吃饭,家里共有N根长度不一的筷子。
第2行包含N个非负整数L[i],描述第i根筷子的长度,输入时L[i]已经从小到大排列。
【输出】
对于每组测试数据输出一行,表示最小的“坏度”值之和。
【样例输入】
1
1 40
1 8 10 16 19 22 27 33 36 40 47 52 56 61 63 71 72 75 81 81 84 88 96 98 103 110 113 118 124 128 129 134 134 139 148 157 157 160 162 164
【样例输出】
23
【数据范围限制】
数据没有梯度。
100%的数据:T=2,0≤ K ≤1000, 3K+24≤ N ≤5000, 1≤ L[i] ≤32000。
【提示】
样例中要组合9套筷子,一种可能的组合是:8,10,16;19,22,27; 61,63,75;71,72,88;81,81,84;96,98,103;128,129,148;134,134,139;157,157,160。
【题解】
比赛时,这道题我只得了0分。T_T (ノ=Д=)ノ┻━┻
鄙视这样的怪人×1,鄙视这样的怪人×2,严重鄙视这样的怪人×∞!
鄙视这样的数据×1,鄙视这样的数据×2,严重鄙视这样的数据×maxlongint!
这题是无聊吧!比赛时,我就想用贪心水分(因为我想不到DP的状态转移方程),结果就……
相信大家第一眼看到道题时都会想到用贪心水分。但很遗憾,这题用贪心是会爆0滴!因为我们不仅要找出两根较短筷子A、B,还要找出不比它们短的一根长筷子C。也就是说,我们不能让选出来的A、B两根筷子筷子找不到它们的伙伴C筷子。我们要用DP做这道题。
我们可以设Fi,j为前i根筷子中挑选j对筷子的最小“坏度”值。那么对于每一根筷子i,我们都可以选或不选(如果要强制选第i根筷子的话,那么最后输出的就是所有的Fi,k+8中的最小值,而不是Fn,k+8了)
首先,我们先要让所有的筷子以长度为关键字从大到小排个序(或者读入时倒着读)。
如果我们选择第i根筷子为A筷子,那么我们所要的B筷子就一定是第i-1根筷子(因为我们不可能像图一这样选,这样选出来的结果绝对没有图二选的那么小,这里所说的一对不包括长筷子C)
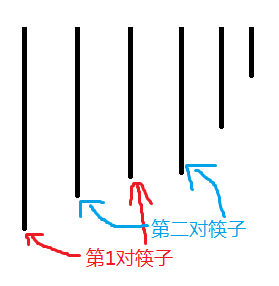
图一
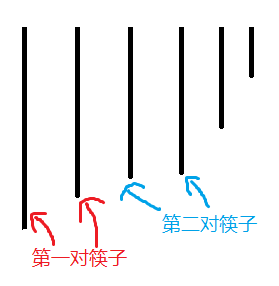
图二
那么我们就可以列出状态转移方程了:
\[f[i][j]=min(f[i][j],f[i-2][j-1]+(l[i-1]-l[i]) * (l[i-1]-l[i])); **( i-2> ( j -1) * 3 )** \]
温馨提示:
-
我们要初始化F数组。记得把所有的Fi,j都初始化为∞,但所有的Fi,0都要初始化为0 (其中1≦i≤n, ,1≤j≤K+8)。一定要注意不要搞错,不然就会错的很奇怪哦!
-
一定要注意循环变量的范围!在DP时,记得外循环是枚举人,内循环是枚举筷子!
-
注意,一共有K+8个人(建议输入后将K加上8)
#include<cstdio>
#include<cstring>
using namespace std;
int f[5010][1020],l[5001];
int min(int x,int y)
{
if(x<y) return x;
else return y;
}
int main()
{
int t,i,j,n,k,choose;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&k,&n);
k=k+8;//输入后直接把K加上8~
for(i=n;i>0;i--)
{
scanf("%d",&l[i]);
f[i][0]=0;//一边输入一遍初始化!
for(j=1;j<=k;j++)
{
f[i][j]=999999999;//不能将f[i][j]赋为maxlongint ,不然当它加上一些数后就会变成负数!
}
}
for(j=1;j<=k;j++)//DP过程,记得外循环枚举人,内循环枚举筷子!
{
for(i=j*3;i<=n;i++)
{
f[i][j]=f[i-1][j];
f[i][j]=min(f[i][j],f[i-2][j-1]+(l[i-1]-l[i])*(l[i-1]-l[i]));
}
}
printf("%d\n",f[n][k]);//输出。没有将K加上8的同学记得输出f[n][k+8]!
}
return 0;
}


