作业2 机器学习相关数学基础

1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。

 

 

2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”，可以word编辑，可做思维导图，可以手写拍照，要求言简意赅、排版整洁。

1.梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)^T,简称grad f(x,y)或者▽f(x,y)。对于在点(x₀,y₀)的具体梯度向量就是(∂f/∂x₀, ∂f/∂y₀)^T.或者▽f(x₀,y₀)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)^T,以此类推。

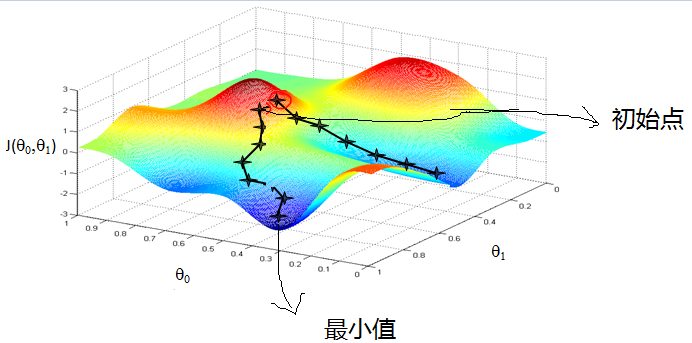
　　　　那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x₀,y₀)，沿着梯度向量的方向就是(∂f/∂x₀, ∂f/∂y₀)^T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x₀, ∂f/∂y₀)^T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

2.梯度下降与上升

　　　　在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

　　　　梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数f(θ)的最小值，这时我们需要用梯度下降法来迭代求解。但是实际上，我们可以反过来求解损失函数 -f(θ)的最大值，这时梯度上升法就派上用场了。

 

3.贝叶斯定理

贝叶斯定理是统计学中非常重要的一个定理，以贝叶斯定理为基础的统计学派在统计学世界里占据着重要的地位，和概率学派从事件的随机性出发不同，贝叶斯统计学更多地是从观察者的角度出发，事件的随机性不过是观察者掌握信息不完备所造成的，观察者所掌握的信息多寡将影响观察者对于事件的认知。