20230317 java.util.TreeMap
介绍
java.util.TreeMappublic class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.Serializable
API
构造器
- TreeMap()
- TreeMap(Comparator<? super K> comparator)
- TreeMap(Map<? extends K, ? extends V> m)
- TreeMap(SortedMap<K, ? extends V> m)
JDK源码是一本标准的数据结构教科书
- 不可变数组String、动态数组StringBuilder
- 顺序表ArrayList、双链表LinkedList
- 队列Queue接口、栈Stack
- 哈希表HashMap、二叉堆PriorityQueue
- 红黑树TreeMap
- 二分、归并、快排、堆排序、模式匹配…
BST树
- 二叉排序树、二叉搜索树
- Binary Sort Tree、Binary Search Tree、BST
- 具有如下性质:
- 定义空树是一个BST
- 左子树所有结点的值均小于根结点的值
- 右子树所有结点的值均大于根结点的值
- 左右子树都是BST(递归定义)
- 中序遍历序列为升序
节点:BstEntry
@Data
public class BstEntry<K, V> implements Map.Entry<K, V> {
K key;
V value;
BstEntry<K, V> left;
BstEntry<K, V> right;
public BstEntry(K key, V value) {
this.key = key;
this.value = value;
}
public BstEntry(K key, V value, BstEntry<K, V> left, BstEntry<K, V> right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
@Override
public K getKey() {
return key;
}
@Override
public V getValue() {
return value;
}
@Override
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
}
映射:BstMap
public class BstMap<K, V>{
private int size;
private BstEntry<K, V> root;
private Comparator<K> comparator;
public BstMap() {
// 不设置比较器,需要K类型实现java.lang.Comparable接口
}
public BstMap(Comparator<K> comparator) {
// 设置比较器,使用比较器比较K类型
this.comparator = comparator;
}
// 方法待补充
}
插入
- int compare(K a,K b),比较关键字a和b的大小
- boolean isEmpty(),判断map是否为空
- V put(K key,V value),添加元素
- 思路:从根节点开始遍历,用key和树节点比较大小
- 如果小于树节点的key,判断树结点的左子树不为空,向树的左子树遍历,否则将新节点连接到树节点的左子节点
- 如果大于树节点的key,判断树结点的右子树不为空,向树的右子树遍历,否则将新节点连接到树节点的右子节点
- 替换树节点的值并返回旧值
- 可以循环或递归
- 参考
java.util.TreeMap#put
- 思路:从根节点开始遍历,用key和树节点比较大小
迭代器
要点:利用中序遍历
- 方案1:递归添加进线性集合,迭代线性集合
- 方案2:非递归,将根节点的左子树压栈,出栈时将出栈节点的右子节点的左子树入栈
- 空间复杂度更低
LeetCode 173. Binary Search Tree Iterator
查找
- BstEntry getEntry(K key): 私有方法,主要查找逻辑
- boolean containsKey(K key): 是否能找到关键字key
- V get(K key): 根据关键字key,返回相应的value
思路:查找与插入类似,假设查找关键字key
- 若根结点的关键字值等于key,成功
- 若key小于根结点的关键字,递归查找左子树
- 若key大于根结点的关键字,递归查找右子树
- 若子树为空,查找不成功
- 参考
java.util.TreeMap#get
查找value
- boolean containsValue(V value): 是否能找到关键字key
思路:需要遍历整个树
- 任意选择先、中、后、层某一种算法框架
- 借助于迭代器
- O(N)
最小、最大节点
- firstEntry, lastEntry
- NavigableMap 接口定义的方法
- firstKey, lastKey
- SortedMap 接口定义的方法
- NavigableMap 的父接口
思路:
- NavigableMap 的父接口
- SortedMap 接口定义的方法
- firstEntry:递归左子节点
- lastEntry:递归右子节点
面试题:寻找BST的最小(最大)节点
删除
- BstEntry<K, V> deleteEntry(): 递归函数
- V remove(K key): 删除关键字key,返回相应的value
- void levelOrder(): 辅助函数,层序输出BST
思路:假设删除节点p,其父节点为f,分如下3种情况进行讨论:
- p是叶子节点,直接删除
- p只有左子树left,直接用p.left替换p(右子树同理)
- p既有左子树left,又有右子树right,找到右子树的最小节点rightMin(需要借助于getFirstEntry,或找到left的最大节点leftMax),用rightMin(或leftMax)的值替换p的值,再根据以上两种情况删除rightMin(或leftMax)
说明:remove方法实现和TreeMap.remove区别很大,TreeMap是红黑树,节点包含parent指针
public V remove(K key) {
// 判断entry是否存在树上
BstEntry<K, V> entry = getEntry(key);
if (entry == null) {
return null;
}
V oldValue = entry.value;
root = deleteEntry(root, key);
size--;
return oldValue;
}
/**
* 删除Entry
* <p>
* <b>Entry必须已存在</b>
*
* @param e 起始节点
* @param key 被删除的Entry key
* @return 新的起始节点:起始节点可能会改变,在被删除的key是起始节点的key时
*/
private BstEntry<K, V> deleteEntry(BstEntry<K, V> e, K key) {
/* 不需要判断非空,因为Entry在树中存在
if (e == null) {
return null;
}*/
int compare = compare(key, e.key);
if (compare < 0) {
// key 小于起始节点,递归到起始节点的左子树
BstEntry<K, V> newLeft = deleteEntry(e.left, key);
// 将左子节点替换成删除后新的左子节点
e.left = newLeft;
} else if (compare > 0) {
// 同左
BstEntry<K, V> newRight = deleteEntry(e.right, key);
e.right = newRight;
} else {
// 找到要删除的节点,跳出递归,返回被替换的节点
// 根据左右子树是否非空分为四种情况
if (e.left == null && e.right == null) {
// 返回null作为替换
e = null;
} else if (e.left != null && e.right == null) {
// e.left 作为替换
e = e.left;
} else if (e.left == null && e.right != null) {
// e.right 作为替换
e = e.right;
} else if (e.left != null && e.right != null) {
// 随机取左子树的最大,或右子树的最小
if ((size & 1) == 0) {
// 替换节点
BstEntry<K, V> rightMin = firstEntry(e.right);
e.key = rightMin.key;
e.value = rightMin.value;
// 删除右子树中最小
BstEntry<K, V> newRight = deleteEntry(e.right, rightMin.key);
e.right = newRight;
} else {
// 替换节点
BstEntry<K, V> leftMax = lastEntry(e.left);
e.key = leftMax.key;
e.value = leftMax.value;
// 删除左子树中最小
BstEntry<K, V> newLeft = deleteEntry(e.left, leftMax.key);
e.left = newLeft;
}
}
}
return e;
}
寻找后继(前趋)节点
分为两种情况:
- 情况1:节点t有右子树,右子树的最小节点p(和getFirstEnrty完全相同)
- 情况2:节点t没有右子树,向上回溯,找到第一个孩子是左子树孩子的父亲p
参考:successor 和 predecessor
思路还是中序遍历
LintCode 448. Inorder Successor in BST
TreeMap.remove
remove 方法根据需要被删除的节点p分为三种情况处理:
- 左右子节点:找到p的后继节点替换p
- 只有左或右子节点:用非空的节点替换p
- 叶子节点:直接删除
AVL树
定义
AVL树是一种自平衡的二叉树,定义如下
- BST
- 左、右子树高度差的绝对值不超过1(平衡因子Balance Factor)
- 空树、左右子树都是AVL
为什么需要AVL树
极端情况下的BST会退化为链表(O(logN) -> O(N))
| BST | TreeMap | |
|---|---|---|
| 随机序列 | OK | OK |
| 升序或降序序列 | Slow | OK |
AVL的插入
四种旋转
- 右旋(RR旋转)
- 左右双旋(LR旋转)
- 左旋(LL旋转)
- 右左双旋(RL旋转)
三个节点的单旋转
右旋(左旋同理)
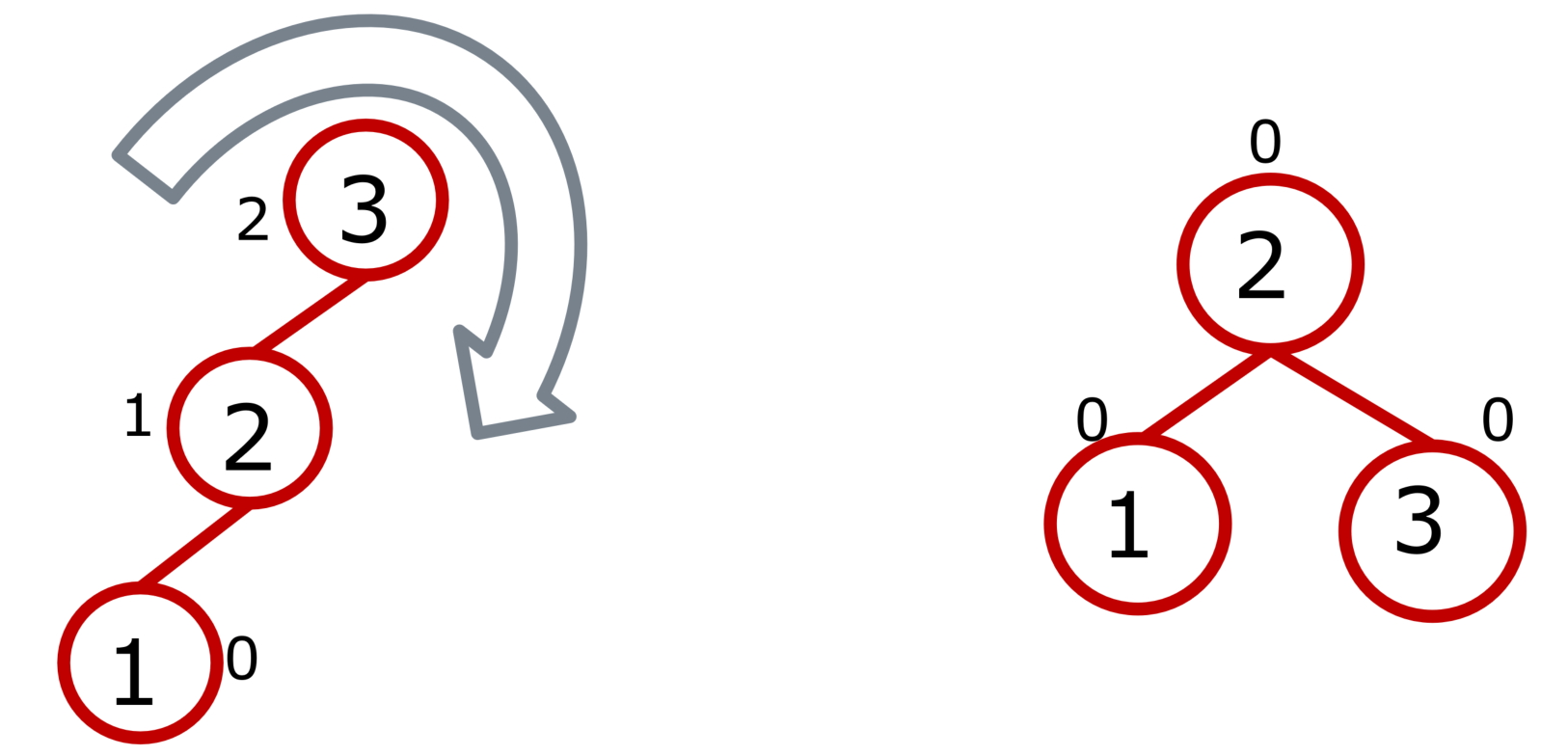
三个节点的双旋转
先左旋,再右旋(先右旋,再左旋同理)
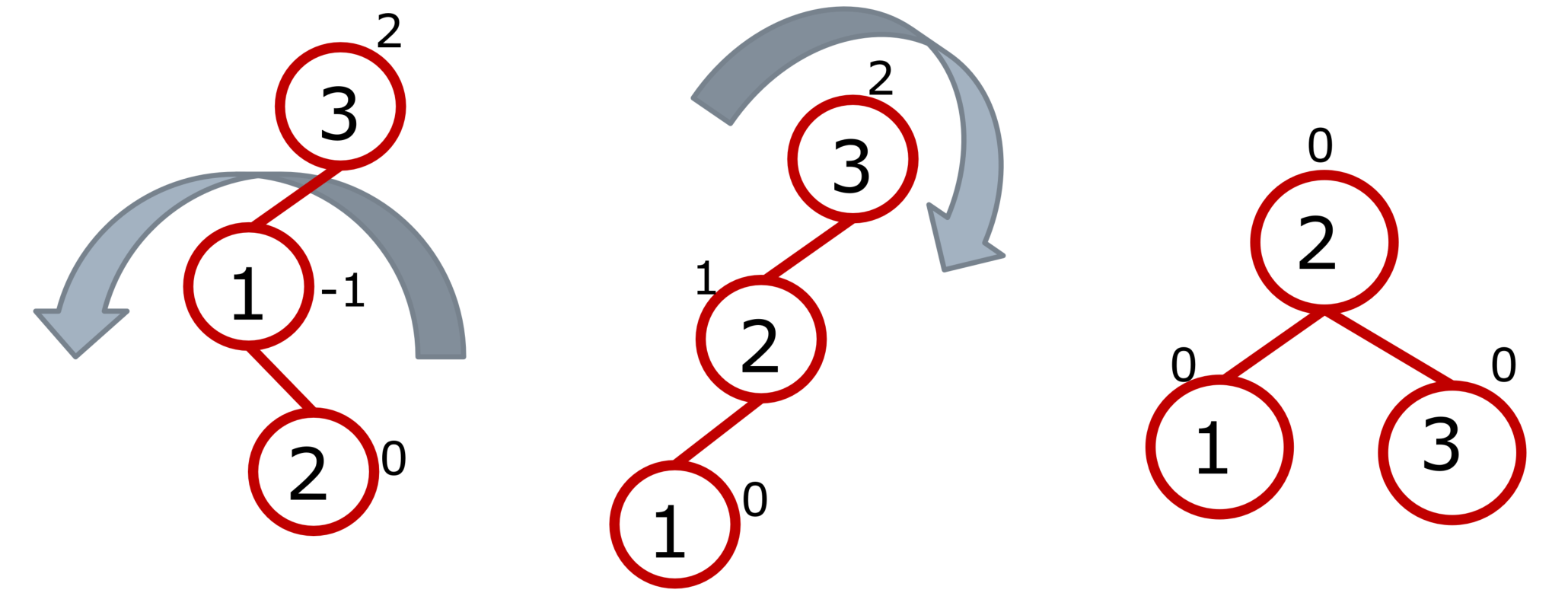
帮助记忆:从3到2是左子节点、右子节点
什么时候需要旋转
- 插入关键字key后,节点p的平衡因子由原来的1或者-1,变成了2或者-2,则需要旋转;
- 只考虑插入key到左子树left的情形,即平衡因子为2
- 情况1:key<left.key, 即插入到left的左子树,需要进行单旋转,将节点p右旋
- 情况2:key>left.key, 即插入到left的右子树,需要进行双旋转,先将left左旋,再将p右旋
- 插入到右子树right、平衡因子为-2,完全对称
自顶向下or自底向上?
- AVL的插入与BST完全相同,都是自顶向下的
- “检测是否平衡并旋转”的调整过程呢?
- 性质2(一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 )决定了:在检测节点p是否平衡之前,必须先保证左右子树已经平衡
- 子问题必须成立 -> 总问题是否成立,自底向上
- 三种思路:
- 有parent指针,直接向上回溯
- 无parent指针,后序遍历框架,递归
- 无parent指针,栈实现非递归
LeetCode 110. Balanced Binary Tree
代码实现
- AVLEnrty增加height属性,表示树的高度,平衡因子可以实时计算
- 单旋转:右旋rotateRight、左旋rotateLeft
- 双旋转:先左后右firstLeftThenRight、先右后左firstRightThenLeft
- 辅助栈stack,将插入时候所经过的路径压栈
- 插入调整函数fixAfterInsertion
- 辅助函数checkBalance,断言AVL树的平衡性,检测算法的正确性
理解:
- 和TreeMap中的实现差别很大,因为TreeMap有parent指针,操作起来更加简单
- stack在put方法中保存新增节点的从顶向下所有父节点
参考 TreeMap#buildFromSorted
算法改进与时间复杂度分析
- 弹栈的时候,一旦发现某个节点的高度未发生改变,则立即停止回溯
- 指针回溯次数,最坏O(logN),最好情况O(1),平均任然是O(logN)
- 旋转次数,无需旋转、单旋转、双旋转,不会超过两次,O(1)
- 时间复杂度:BST的插入logN+指针回溯logN+旋转O(1)=O(logN)
- 空间复杂度:有parent为O(1),无parent为O(logN)
AVL的删除
- 类似插入,假设删除了p右子树的某个节点,引起了p的平衡因子d[p]=2,分析p的左子树left,三种情况如下:
- 情况1:left的平衡因子d[left]=1,将p右旋
- 情况2:left的平衡因子d[left]=0,将p右旋
- 情况3:left的平衡因子d[left]= -1,先左旋left,再右旋p
- 删除了p左子树的某个节点,即d[p]= -2的情形,与d[p]=2对称
情况一:
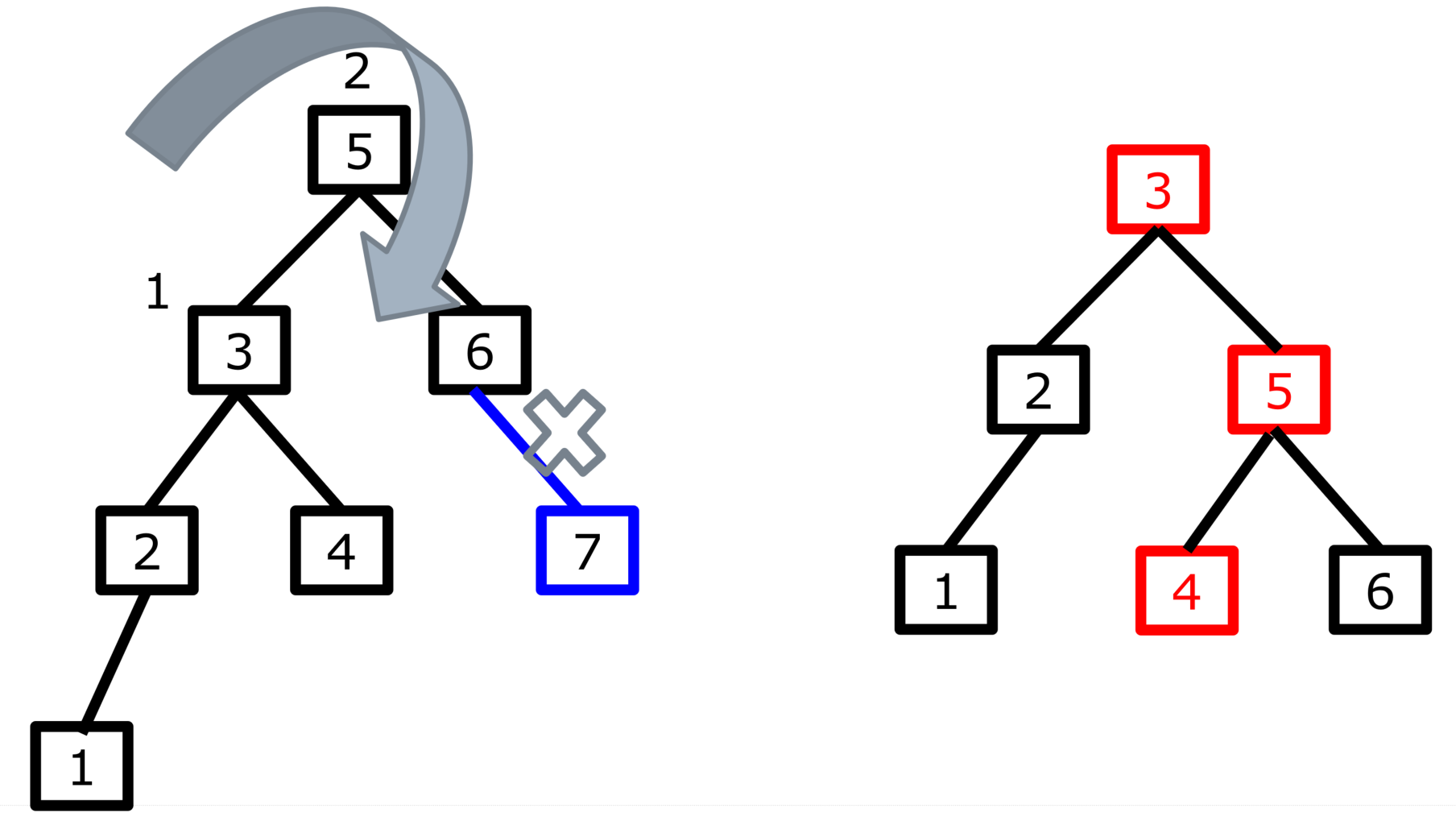
情况二:
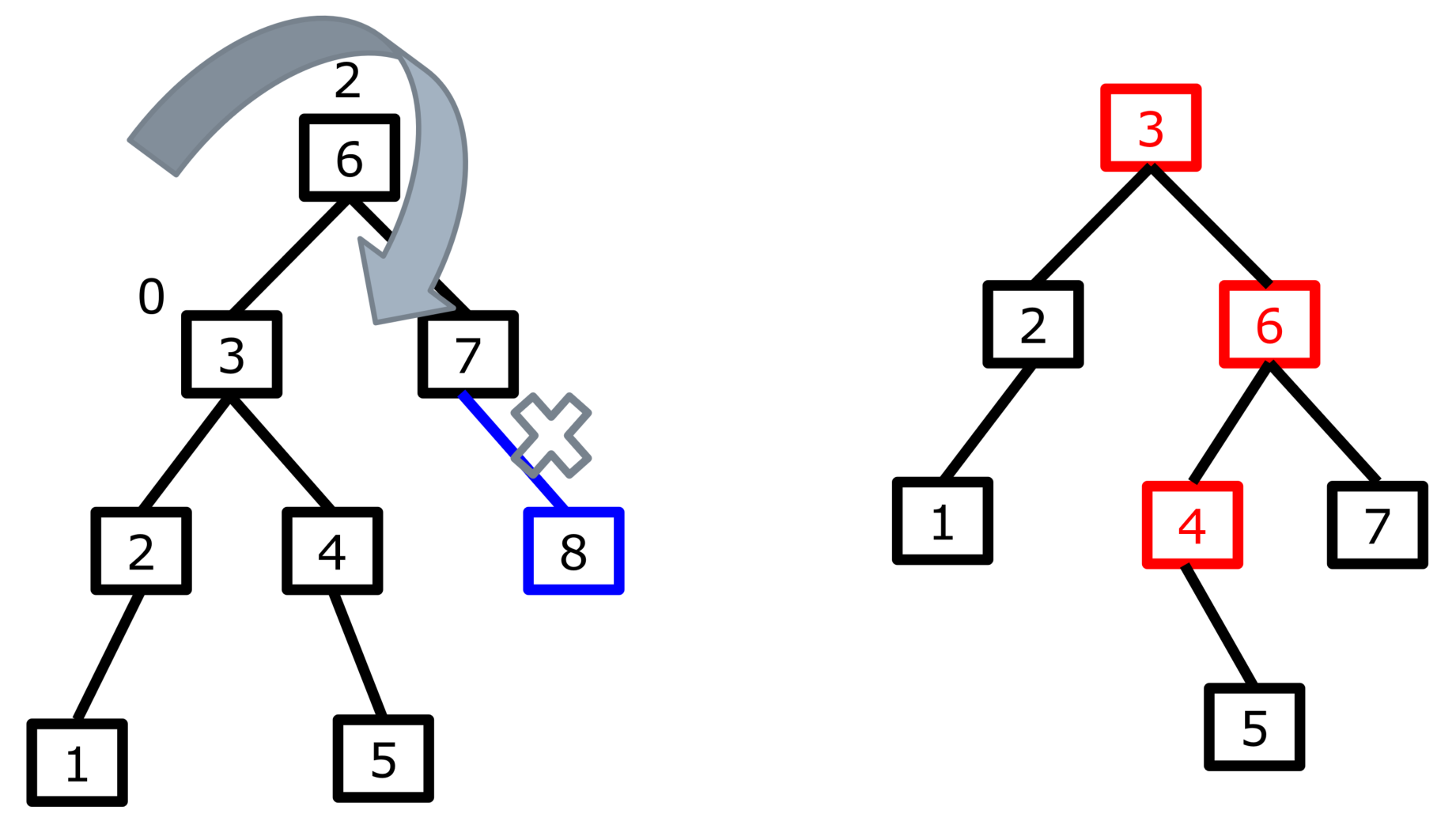
情况三:
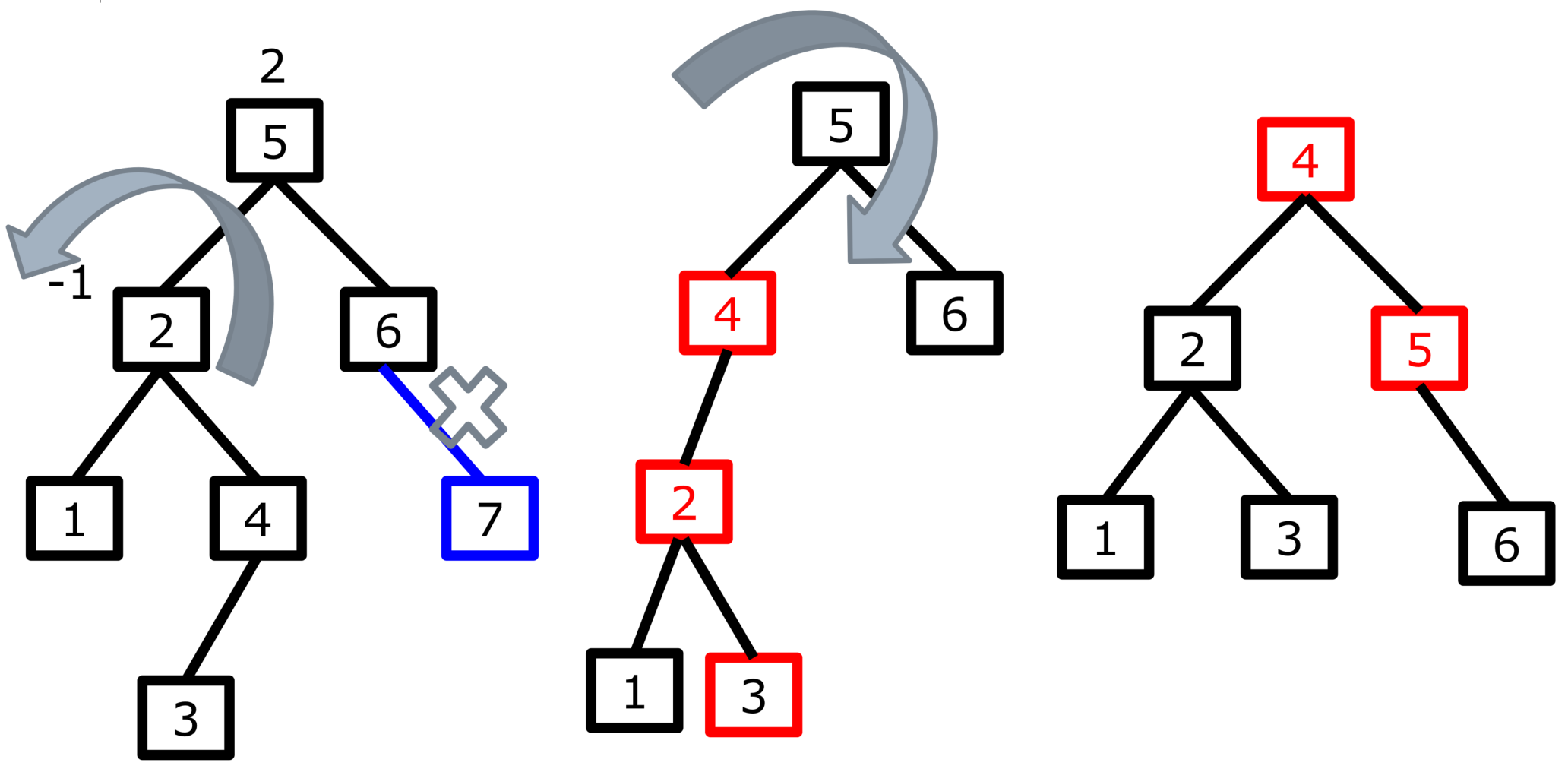
代码实现
- fixAfterDeletion:调整某个节点p
- deleteEntry直接调用fixAfterDeletion
理解:
- deleteEntry是递归实现,每次递归都会调用fixAfterDeletion,很难理解,需要调试
- 和
TreeMap.fixAfterDeletion比较:TreeMap中包含parent引用,
BRT树
概念
红黑树、RedBlackTree、RBT
5大性质:
- 每个结点要么是红的,要么是黑的
- 根结点是黑的
- 定义NULL为黑色
- 如果某个子结点是红色,那么它的俩个儿子都是黑色,且父节点也必定是黑色
- 对于任一结点而言,它到叶结点的每一条路径都包含相同数目的黑色结点
性质5称为黑高、BlackHeight、BH
2个补充性质:
- RBT是一个BST
- 任意一颗以黑色节点为根的子树也必定是一颗红黑树(与BST、AVL的递归定义类似)
结论:
- 红黑树不像AVL一样,永远保持绝对平衡
- 相对平衡
- 若\(H(left) \ge H(right)\),则:\(H(left) \le 2*H(right)+1\),但\(BH(left)===BH(right)\),H(left)<H(right)同理
- 定理:N个节点的RBT,最大高度是2log(N+1)
- 严格证明参考CLRS(算法导论)
- 查询效率AVL略好于RBT
只需研究
- RBT的插入调整:fixAfterInsertion源码
- case1、case2、case3
- RBT的删除调整:fixAfterDeletion源码
- case1、case2、case3、case4
直接研究TreeMap的源码,不再自己实现
自顶向下or自底向上
- 与AVL类似,在调整某个节点p之前,必须先保证p的左子树left、右子树right都已经是RBT
- 多个子问题成立 -> 某个总问题成立
- 插入调整、删除调整均是 自底向上 bottom up
RBT的插入
参考:TreeMap#fixAfterInsertion
- 若插入的节点为黑色,肯定违反性质5
- 只能插入红色节点,可能违反性质4,继续调整
参考代码中的:
// 将插入节点的颜色设置为红色
x.color = RED;
...
// 将根节点颜色设置为黑色
root.color = BLACK;
插入调整
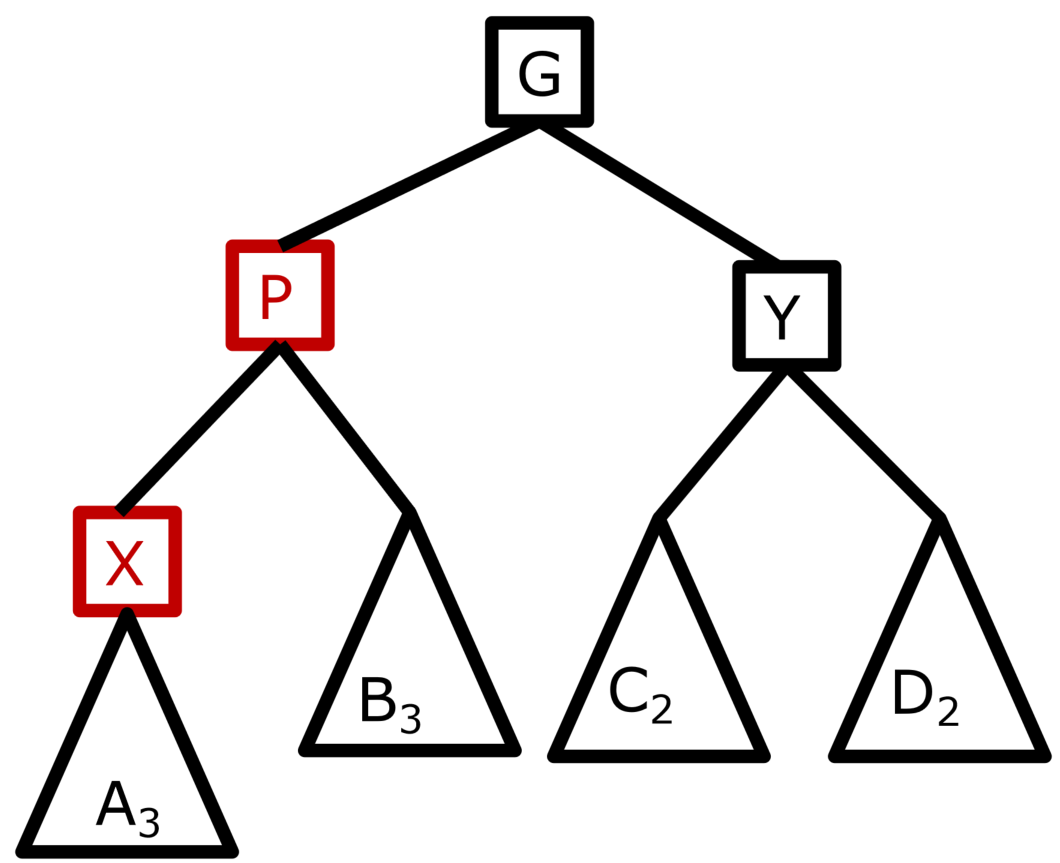
考虑插入到左子树的情况,规定如下标记:
- 正在处理的节点X,也叫子节点
- 父节点P
- 爷爷节点G
- 叔叔节点Y
- A3表示黑高为3的红黑树
插入调整算法的正确性证明:
-
每将节点进行染色、旋转操作,我们需要考虑:
- 是否会引起左右子树BH不一致,即是否满足性质5
- 有无继续破坏性质4的可能
-
无需调整的情况为:
- X为根节点,将X由红染黑,简称rootOver
- 父节点P为黑色,BlackParentOver,简称bpOver
-
仅仅需要考虑父节点P为红色的情形,由于性质4,爷爷节点G必定为黑色,分为三种情况:
- case1: Y为红色,X可左可右;P、Y染黑,G染红,X回溯至G
- case2: Y为黑色,X为右孩子;左旋P,X指向P,转化为case3
- case3: Y为黑色,X为左孩子;P染黑,G染红,右旋G,结束
-
结论:RBT的插入调整最多旋转2次
无需调整
- 越界
- X是根节点
- 父节点P的颜色为黑,必定满足性质4
也就是代码中的
while (x != null && x != root && x.parent.color == RED) {
case1
- 条件:P为G的左孩子,Y为红色,X可左可右
- 处理方式:P、Y染黑,G染红,X回溯至G
- 条件简称:红左父、红叔、红左右子
- 处理方式简称:父叔都变黑、爷变红、子变爷
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
case1的正确性证明:
- 经过case1调整之后:
- 显然X、P、Y、G的关系均满足性质4
- X的BH未改变 -> P满足性质5
- P、Y的BH同时增加了1 -> G满足性质5
- G的BH未改变 -> 整个RBT满足性质5
- G是红色,可能违反性质2、性质4,需要继续调整
case1的转化:
- 由于G是一个红色节点,故case1可转化为:
- case1
- case2
- case3
- rootOver,把根节点由红染黑,结束调整,此时整个红黑树的BH增加1,这是唯一增加整个树BH的情形
case2
- 条件: P为G的左孩子,Y为黑色,X为右孩子
- 处理方式:左旋P,X指向P,转化为case3
- 条件简称:红左父,黑叔,红右子
- 处理方式简称:左旋父、子变父、变为case3
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
case2的正确性证明:
- 经过case2调整之后:
- P左右子树的BH未改变 -> P满足性质5
- X左右子树的BH未改变 -> X满足性质5
- X、Y的BH均未改变 -> G满足性质5
- G的BH未改变 -> 整个RBT满足性质5
- P、X的关系任然违反性质4,需要继续调整
case2的转化:
- case2只能转化为case3
- case2不会引起BH增加
case3
- 条件:P为G的左孩子,Y为黑色,X为左孩子
- 处理方式:P染黑,G染红,右旋G,结束
- 条件简称:红左父,黑叔,红左子
- 处理方式简称:父变黑、爷变红、右旋爷
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
case3的正确性证明:
- 经过case3调整之后:
- G左右子树的BH未改变 -> G满足性质5
- P左右子树的BH未改变 -> P满足性质5
- P的BH未改变 -> 整个RBT满足性质5
- P的颜色为黑色,必定满足性质2、性质4,算法结束
case3的转化:
- case3无需转化,也不会引起BH增加
AVL插入 VS RBT的插入
- 插入元素都是BST的插入,区别在于调整
- 旋转次数:AVL与RBT均是O(1)
- 指针回溯次数,最好情况:
- 很早就遇到单旋或双旋的情况,为O(1)
- 很早就遇到case2或case3,为O(1)
- 指针回溯次数,最坏情况:
- 回溯至根节点才发现平衡因子大于1,为logN
- 不断执行case1,直到根节点,但每次向上回溯两层,为logN/2
- 插入效率:RBT略好于AVL
- 查询效率:AVL略好于RBT
RBT的删除
- 参考
TreeMap.fixAfterDeletion - 删除的情况比插入多,需要配合代码调试查看
- 有时传入
fixAfterDeletion的参数不是要被删除的节点,而是它的后继结点,调试时,需要从deleteEntry开始
- 有时传入
RBT的删除原则
- 删除红色节点,不会影响BH,也不会违反性质4,无需调整
- 删除黑色节点,节点所在子树的BH--,需要调整
RBT的删除调整
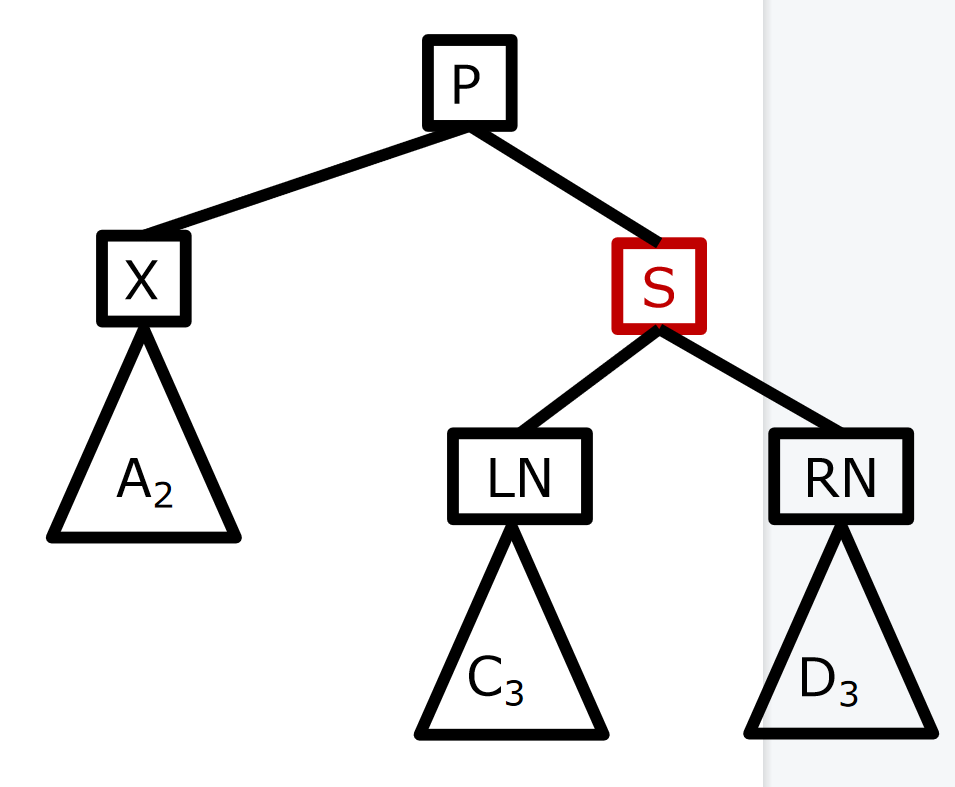
- 考虑删除左子树的情况,规定如下标记:
- 正在处理的节点X(不一定是正在被删除的节点)
- 父节点P
- 兄弟节点sib,简称S
- 左侄leftNephew,简称LN
- 右侄rightNephew,简称RN
- 需要删除的节点X为红色,直接删除X
- 其它无需调整的情况为:
- 当前X为根节点,无论root什么颜色,都将root染黑,rootOver
- 当前X为红色,将X染黑,结束,redOver
- 删除左孩子X,需要调整的分为四种情况:
- case1: S为红色;S染黑,P染红,左旋P
- case2: S为黑色,黑LN,黑RN;S染红,X回溯至P
- case3: S为黑色,红LN,黑RN;LN染黑,S染红,右旋S
- case4: 黑S,LN随意,红RN;S变P的颜色,P和RN染黑,左旋P
删除调整算法的正确证明:
- 每将节点进行染色、旋转操作,都需要考虑:
- 是否违反性质5,如:
- X的BH只能不变或增加,否则X的BH将比S的更小
- 是否违反性质4的,如果违反,染黑还是继续回溯?
- 是否违反性质5,如:
无需调整
- 删除的X本身就是红色节点,直接删除
// 被删除的节点是黑色时,才需要调整 if (p.color == BLACK) fixAfterDeletion(replacement); - 回溯指针时遇到的情形:
- X为根节点,无论root什么颜色,都将root染黑,将根节点染黑同时满足性质2、4、5,简称 rootOver
- X为红色,将X染黑,简称 redOver
while (x != root && colorOf(x) == BLACK) { ... } setColor(x, BLACK);
case1
- 条件:S为红色
- 隐含条件:由于性质4,P、LN、RN必定都为黑色
- 处理方式:S染黑,P染红,左旋P,LN成为新的sib
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
case1的正确性证明,经过case1调整之后:
- 符合性质4
- BH(X)比BH(LN)少1 -> P违反性质5
- P违反性质5 -> S违反性质5
- 需要继续调整X
case1的转化情况:
- case1可转化为:
- case2-2
- case3
- case4-1、case4-2
- case1不会引起BH的变化
case2
- case2-1条件:S、LN、RN均为黑色,P为黑色
- case2-2条件:S、LN、RN均为黑色,P为红色
- 处理方式相同:S染红,X回溯至P
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
case2-1
case2-1的正确性证明,经过case2-1调整之后:
- 符合性质4
- S的BH减少了1,BH(X)==BH(S) -> P符合性质5
- P的BH减小了1 -> 整个RBT违反性质5
- 需要继续调整P
case2-1的转化情况
- 由于P是黑色,故case2-1可转化为任意case:
- case1
- case2-1、case2-2
- case3
- case4-1、case4-2
- 若P为根节点,则执行case2-1会引起BH的减小,
这是唯一减小整个红黑树BH的情形
case2-2
- case2-2的正确性证明
- 经过case2-2调整之后:
- BH(S)减少了1,BH(X)==BH(S) -> P符合性质5
- P的BH减小了1 -> 整个RBT违反性质5
- P与S的关系违反了性质4
- 调整策略:
- redOver
- 直接将P染黑 -> BH(P)++ -> 满足性质4且RBT平衡
case2-2的转化情况
- case2-2只能转化为redOver并结束调整
case3
- 条件:S为黑色,LN为红色,RN为黑色
- 处理方式:LN染黑、S染红,右旋S,S指向LN
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
case3的正确性证明,经过case3调整之后:
- S的左右子树BH相等 -> S符合性质5
- LN的左右子树BH相等 -> LN符合性质5
- X的BH仍然比LN的BH少1 -> P违反性质5
- 需要继续调整X
case3的转化情况
- case3可转化为case4-1、case4-2
case4
- 条件:S为黑色,P可红可黑,RN为红色
- case4-1:LN为红色
- case4-2:LN为黑色
- 处理方式:S的颜色设置为与P相同,P染黑,RN染黑,左旋P,X指向根节点,rootOver
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
case4的正确性证明,经过case4调整之后:
- 染黑之后的P正好填补了左子树缺少的一个BH
- RN染黑,正好填补了空缺的黑S,右子树的BH不变
- BH(P)==BH(RN) -> S符合性质5
- 以S为根的子树BH和删除前一样 -> 整个RBT平衡
- 没有任何违反性质4的节点
- rootOver
case4的转化情况
- rootOver,无需转化
转化情况与旋转次数
- 完整的case转化情况:
- case1 -> case2-2、case3、case4
- case2-1 -> case1、case2-1、case2-2、case3、case4
- case2-2 不可转化
- case3 -> case4
- case4-1 不可转化
- case4-2 不可转化
- RBT的删除调整最多旋转3次
- 如:case1 -> case3 -> case4
AVL的删除 VS RBT的删除
- 删除节点都是BST的删除,区别在于调整
- 旋转次数:AVL与RBT均是O(1)
- 指针回溯次数,最好情况:
- 类似插入,可通过优化提前结束递归(课后思考),为O(1)
- 很早就遇到case1、case2-2、case3或case4,为O(1)
- 指针回溯次数,最坏情况:
- 回溯至根节点才发现平衡因子大于1,为logN
- 不断执行case2-1,直到根节点,为logN;但是,RBT大部分形态下是红黑相间的,一直遇不到红色节点的情况很少见
- 删除效率:RBT略微好于AVL
进一步细化case
左:
- leftCase1: S为红色;S染黑,P染红,左旋P
- leftCase2-1: 黑S,黑LN,黑RN,黑P;S染红,X回溯至P
- leftCase2-2: 黑S,黑LN,黑RN,红P;S染红,X回溯至P
- leftCase3: 黑S,红LN,黑RN;LN染黑,S染红,右旋S
- leftCase4-1: 黑S,红LN,红RN;S以父为名,P和RN染黑,左旋P
- leftCase4-2: 黑S,黑LN,红RN;S以父为名,P和RN染黑,左旋P
右,对称操作:
- rightCase1: S为红色;S染黑,P染红,右旋P
- rightCase2-1: 黑S,黑LN,黑RN,黑P;S染红,X回溯至P
- rightCase2-2: 黑S,黑LN,黑RN,红P;S染红,X回溯至P
- rightCase3: 黑S,红RN,黑LN;RN染黑,S染红,左旋S
- rightCase4-1: 黑S,红LN,红RN;S以父为名,P和LN染黑,右旋P
- rightCase4-2: 黑S,红LN,黑RN;S以父为名,P和LN染黑,右旋P



