20230406 8.2. 拓扑排序

概念

• 拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序
• 获得一个拓扑序的过程就是拓扑排序
• AOV (Activity On Vertex) 如果有合理的拓扑序，则必定是 有向无环图（Directed Acyclic Graph, DAG）

void TopSort()
{ 
    for ( 图中每个顶点 V )
    if ( Indegree[V]==0 )
        Enqueue( V, Q );
    while ( !IsEmpty(Q) ) {
        V = Dequeue( Q );
        输出V，或者记录V的输出序号; cnt++;
        for ( V 的每个邻接点 W )
        if ( ––Indegree[W]==0 )
        Enqueue( W, Q );
    }
    if ( cnt != |V| )
        Error( “图中有回路” );
}

• 此算法可以用来检测有向图是否 DAG（有向无环图）
• T = O( |V| + |E| )

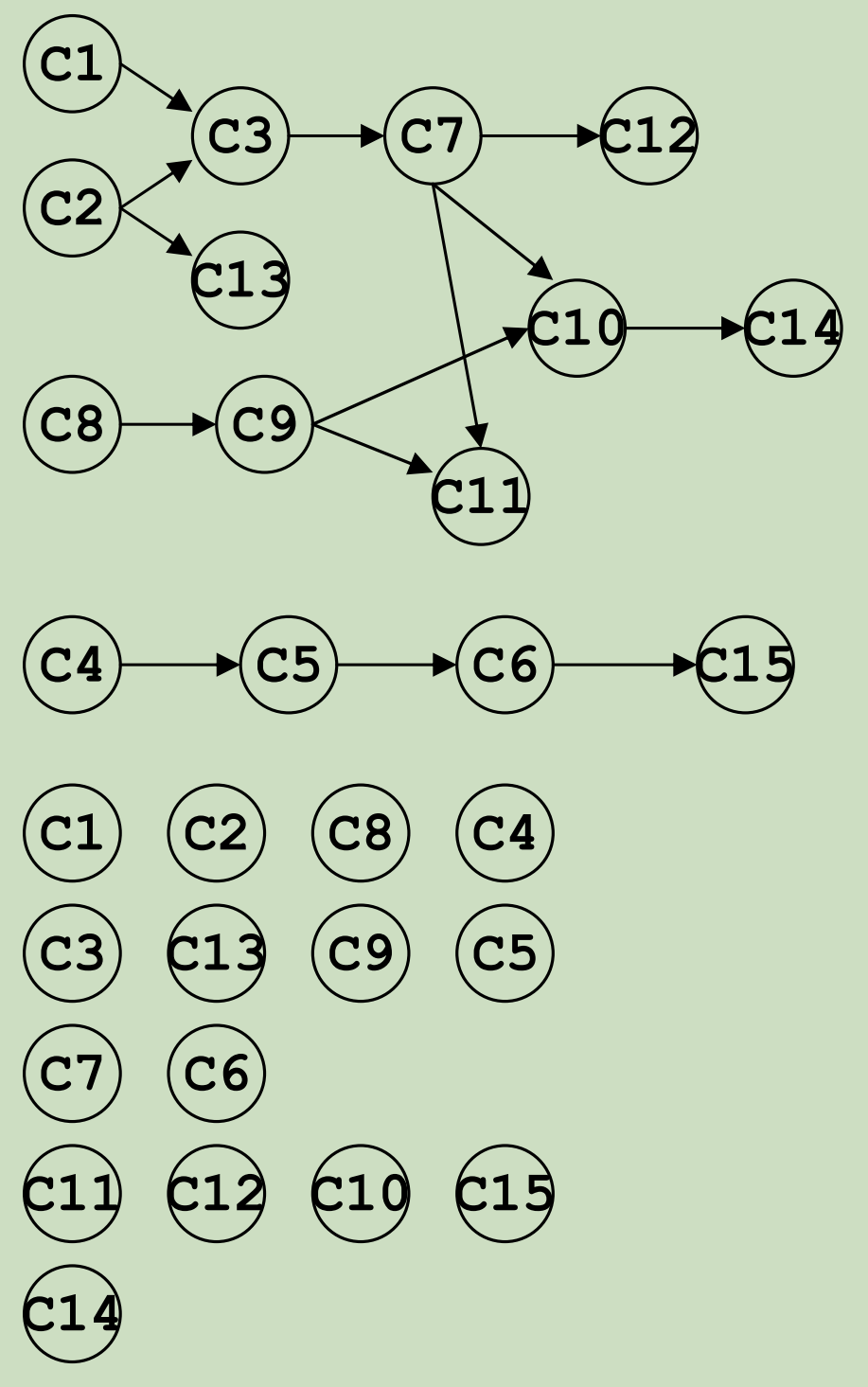
例题：计算机专业排课

AOV (Activity On Vertex) 网络

课程号	课程名称	预修课程
C1	程序设计基础	无
C2	离散数学	无
C3	数据结构	C1, C2
C4	微积分（一）	无
C5	微积分（二）	C4
C6	线性代数	C5
C7	算法分析与设计	C3
C8	逻辑与计算机设计基础	无
C9	计算机组成	C8
C10	操作系统	C7, C9
C11	编译原理	C7, C9
C12	数据库	C7
C13	计算理论	C2
C14	计算机网络	C10
C15	数值分析	C6

/**
    * 拓扑排序
    */
public void topSort() {
    // 计算每个节点的入度
    int[] inDegress = new int[size];
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            if (edges[i][j] == 1) {
                inDegress[j]++;
            }
        }
    }

    // 将入度为0的节点加入队列
    Queue<Integer> queue = new LinkedList<>();
    for (int i = 0; i < inDegress.length; i++) {
        if (inDegress[i] == 0) {
            queue.offer(i);
        }
    }

    List<Integer> retList = ListUtil.toList();
    while (!queue.isEmpty()) {
        Integer v = queue.poll();
        retList.add(v);

        // 将临接点的入度减一，如果入度为0，加入队列
        for (int i = 0; i < size; i++) {
            if (edges[v][i] == 1 && inDegress[i] > 0) {
                if (--inDegress[i] == 0) {
                    queue.offer(i);
                }
            }
        }
    }

    if (retList.size() != size) {
        throw new RuntimeException("图中有回路");
    }
    Console.log(retList);


}

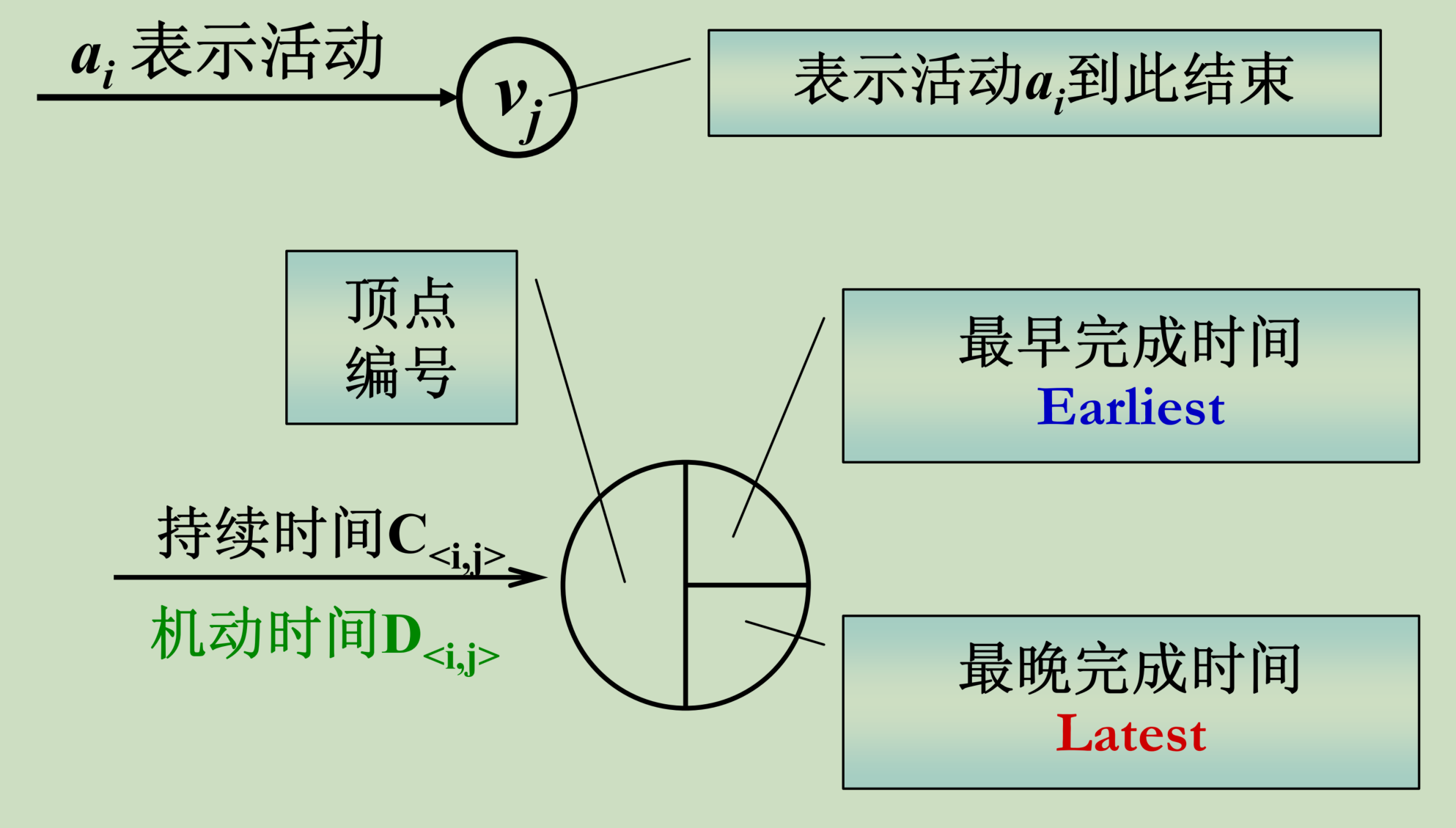
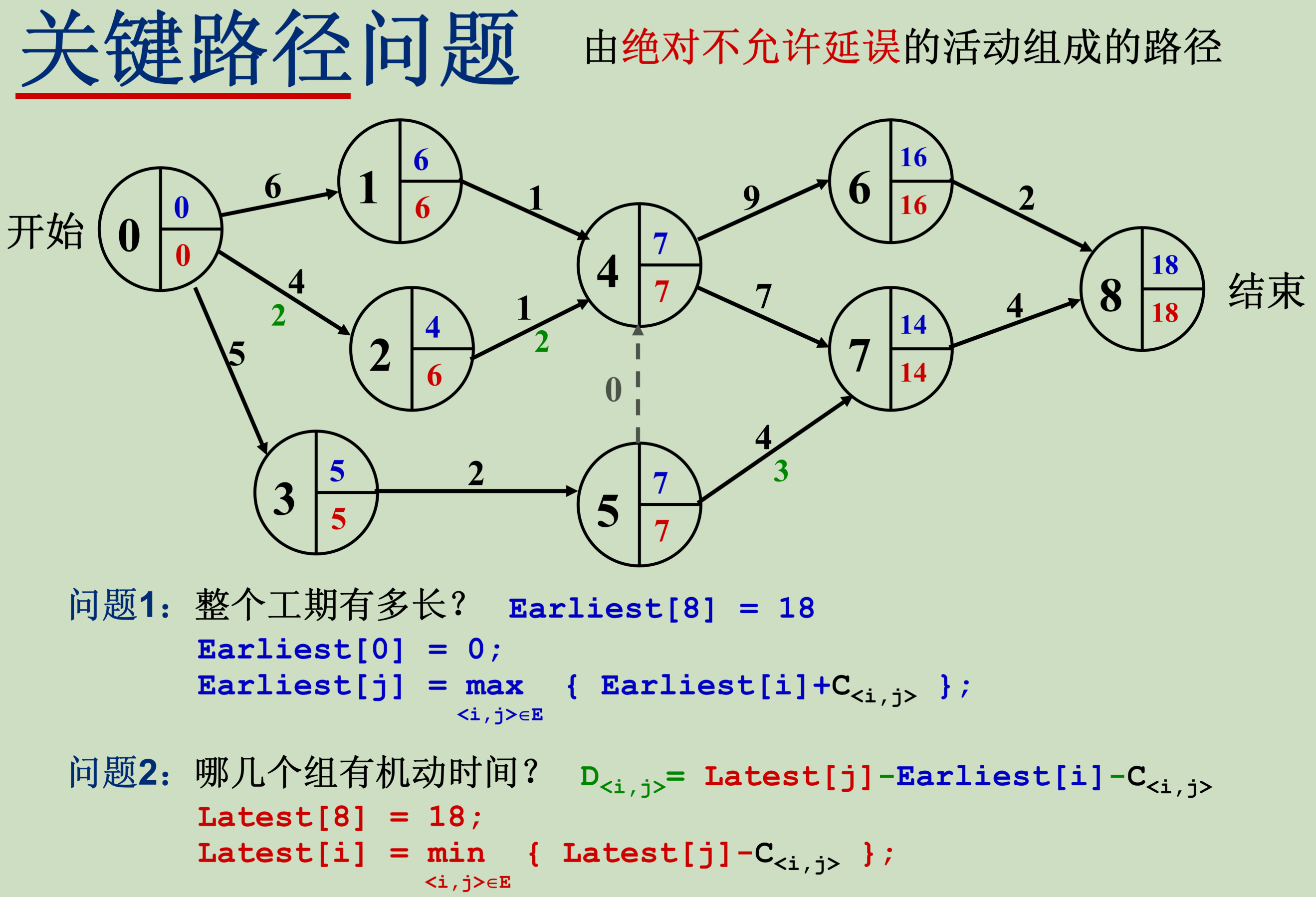
关键路径问题

• AOE (Activity On Edge) 网络
• 一般用于安排项目的工序