归并排序算法

　　归并排序就是将未排序的数组进行对半划分成两个数组，划分后的数组只有原来数组的一半数量的元素。然后在对划分的两个数组再继续划分，循环此操作，直到划分的数组中只有一个元素时停止划分，然后对于划分完成的数组进行归并排序操作。将两个已经划分完成的数组合并成一个有序的数组，直到最后合并成一个包含所有元素的数组，合并排序操作完成。下面以图形来演示下归并排序的过程。

　　假设有一个未排序数组：｛3，2，4，1｝，下面为数组的划分过程，先将数组对半划分为｛3，2｝和｛4，1｝两个数组。然后在对这两个数组进行划分最后得到｛3｝，｛2｝，｛4｝，｛1｝四个数组，划分完成。
 

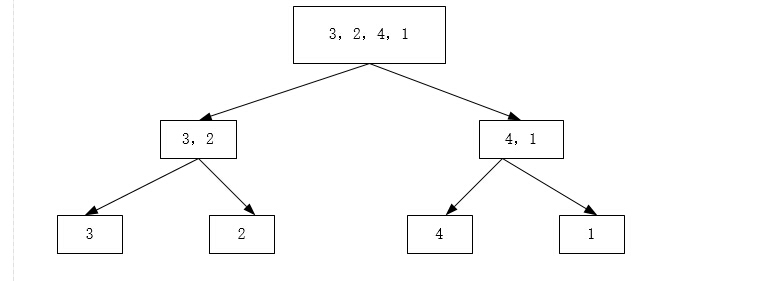
　　接下来对数组进行归并，先将｛3｝和｛2｝这两个数组合并成一个有序的数组｛2，3｝，同理对4，1进行相同的操作，得到｛1，4｝，然后在将合并好的这两个有序数组进行合并，最后合并成｛1，2，3，4｝，归并完成。

 

　　归并排序算法用java代码实现如下：

       public static void MergeSort(int[] array,int head,int tail){
            // 判断数组的头部索引是否小于尾部索引
            if(head < tail){
                int middle = (head+tail)/2;
                MergeSort(array,head,middle);
                MergeSort(array,middle+1,tail);
                Merge(array,head,middle,tail);
            }    
        }

        public static void Merge(int[] array, int head, int middle, int tail) {
            // TODO Auto-generated method stub
            int[] temp = new int[tail - head + 1];
            int a = head;
            int b = middle + 1;
            int i = 0;
            // 对于两个数组中的数进行比较，将较小的值存放在临时数组中
            while(a <= middle && b <=tail){
                
                if(array[a] < array[b]){
                    temp[i++] = array[a++];   
                }
                else{
                    temp[i++] = array[b++];
                }  
            }
            
            // 将未参与比较的数组中的数添加到临时数组中
            while(a <= middle){
                temp[i++] = array[a++];
            }
            
            while(b <= tail){
                temp[i++] = array[b++];
            }
           
            // 将排好序的数组放回到array数组中
            System.arraycopy(temp,0,array,head,tail - head + 1);
        }

　　归并排序的时间复杂度为：O（nlogn），空间复杂度为：O（n）。