信息论、交叉熵
参考博客:http://blog.csdn.net/rtygbwwwerr/article/details/50778098
信息论
主要研究对一个信号包含信息的多少进行量化。
信息论的基本想法是一个不太可能的事件居然发生了,要比一个非常可能的事件发生,能提供更多的信息。例如一则消息说:“今天早上太阳升起”,这是一件很平常的事情, 信息量是如此之少以至于没有必要发送,但一条消息说:“今天早上有日食”,这件事发生概率很小,信息量就很丰富。
在机器学习中,主要使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。
我们想要通过这种基本想法来量化信息。特别地,
• 非常可能发生的事件信息量要比较少,并且极端情况下,确定能够发生的事件应该没有信息量。
• 较不可能发生的事件具有更高的信息量。
• 独立事件应具有倍增量的信息。例如,投掷的硬币两次正面朝上传递的信息量,应该是投掷一次硬币正面朝上的信息量的两倍。
为了满足上述三个性质,我们定义一个事件 $X=x$ 的 自信息(self-information)为:$${\text{I}}(x) = - \log P(x)$$
在这里,我们用 log 来表示自然对数,其底数为 e(这符合Python中numpy包的规则)。因此我们定义的$I(x)$的单位是 奈特(nats)。
一奈特是以$\frac{1} {e}$的概率观测到一个事件时获得的信息量。其他的材料中使用底数为 2 的对数,单位是 比特(bit)或者 香农(shannons);通过比特度量的信息只是通过奈特度量信息的常数倍。
熵
熵是信息量的期望值:$H(x) = E[I(x)]$
通常使用香农熵(Shannon entropy)来对整个概率分布中的不确定性总量进行量化:$$H(X) = {E_{P}}[I(x)] = - {E_{P}}[\log P(x)]$$
离散时:$H(X) = - {E_{P}}[\log P(x)] = - \sum\limits_{x \in X} {p(x)\log p(x)}$
连续时:$H(X) = - {E_{P}}[\log P(x)] = - \int\limits_{x \in X} {p(x)\log p(x)dx}$
为了保证有效性,这里约定当$p(x) \to 0$时,有$p(x)\log p(x) \to 0$。
一个分布的香农熵是指遵循这个分布的事件所产生的期望信息总量。
当X 是连续的,香农熵被称为微分熵(differential entropy)。
当X为0-1分布时,熵与概率p的关系如下图(二值随机变量的香农熵):
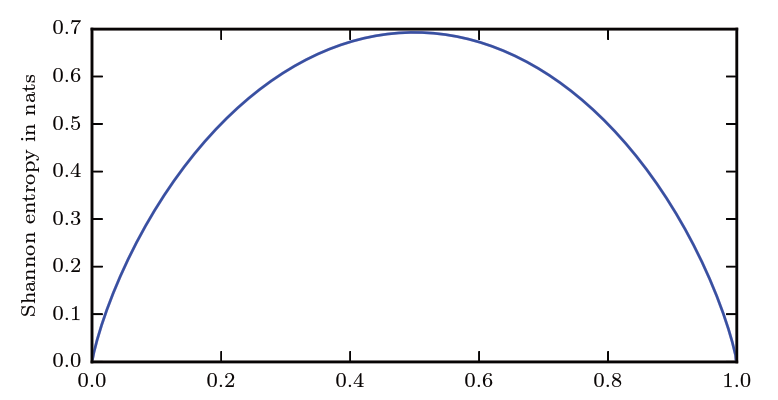
该图说明了更接近确定性的分布(两边)具有较低的香农熵,而更接近均匀分布的分布(中间)具有较高的香农熵。
水平轴是 p,表示二值随机变量等于 1 的概率。熵由$H(x) = (p - 1)\log (1 - p) - p\log p$给出。
-
- 当 p 接近 0 时,分布几乎是确定的,因为随机变量几乎总是 0。
- 当 p 接近 1 时,分布也几乎是确定的,因为随机变量几乎总是 1。
- 当 p = 0.5 时,熵是最大的, 因为分布在两个结果(0 和 1)上是均匀的。
相对熵(relative entropy)
如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x) ,我们可以使用KL散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异(也称为相对熵):
$${D_{KL}}(P||Q) = {E_{P}}[\log \frac{{P(x)}} {{Q(x)}}] = {E_{P}}[\log P(x) - \log Q(x)]$$
香农熵(H(X))给出了对依据P(x)分布生成的符号进行编码所需的比特数在平均意义上的最小值 (当对数底数不是 2 时,单位将有所不同)。
${D_{KL}}(P||Q)$表示在真实分布为P的前提下,使用Q分布进行编码相对于使用真实分布P进行编码(即最优编码)所多出来的bit数。
交叉熵(cross entropy)
$$H(P,Q) = H(P) + {D_{KL}}(P||Q) = - {E_{P}}[\log Q(x)]$$
交叉熵与相对熵仅相差了H(P),当p已知时,可以把H(P)看做一个常数,此时交叉熵与KL距离在行为上是等价的,都反映了分布P(x),Q(x)的相似程度。
最小化交叉熵等于最小化KL距离。它们都将在P=Q时取得最小值H(P)(P=Q时KL距离为0),因此有的工程文献中将最小化KL距离的方法称为Principle of Minimum Cross-Entropy (MCE)或Minxent方法。


