系统的响应与解
各种响应的概念
单位冲激响应:以单位冲激信号$\delta (t)$作激励时,系统产生的零状态响应,以h(t)表示。
单位阶跃响应:以单位阶跃信号u(t)作激励,系统产生的零状态响应,以g(t)表示。
自由响应:也称固有响应,由系统本身特性决定,与外加激励形式无关。对应于齐次解。
强迫响应:形式取决于外加激励。对应于特解。
暂态响应:是指激励信号接入一段时间内,完全响应中暂时出现的有关成分,随着时间t 增加,它将消失。
稳态响应:由完全响应中减去暂态响应分量即得稳态响应分量。(系统方程的齐次解)
零输入响应:没有外加激励信号的作用,只由起始状态(起始时刻系统储能)所产生的响应。
零状态响应:不考虑原始时刻系统储能的作用(起始状态等于零),由系统的外加激励信号产生的响应。
瞬态响应指$t \to \infty $时,响应趋于零的那部分响应分量。
稳态响应指$t \to \infty $时,响应不为零的那部分响应分量。
解的概念
齐次解:假设与微分阶数有关的变量为y,而y是x的函数,只含x或常数的项为0对应的微分方程(例如:$\frac{d^2}{dt^2}y(t)+3\frac{d}{dt}y(t)+2y(t)=f(t),f(t)=0$)的解即为微分方程的齐次解
特解:与齐次解对应,$f(t) \ne 0$对应微分方程的解
主要关系图
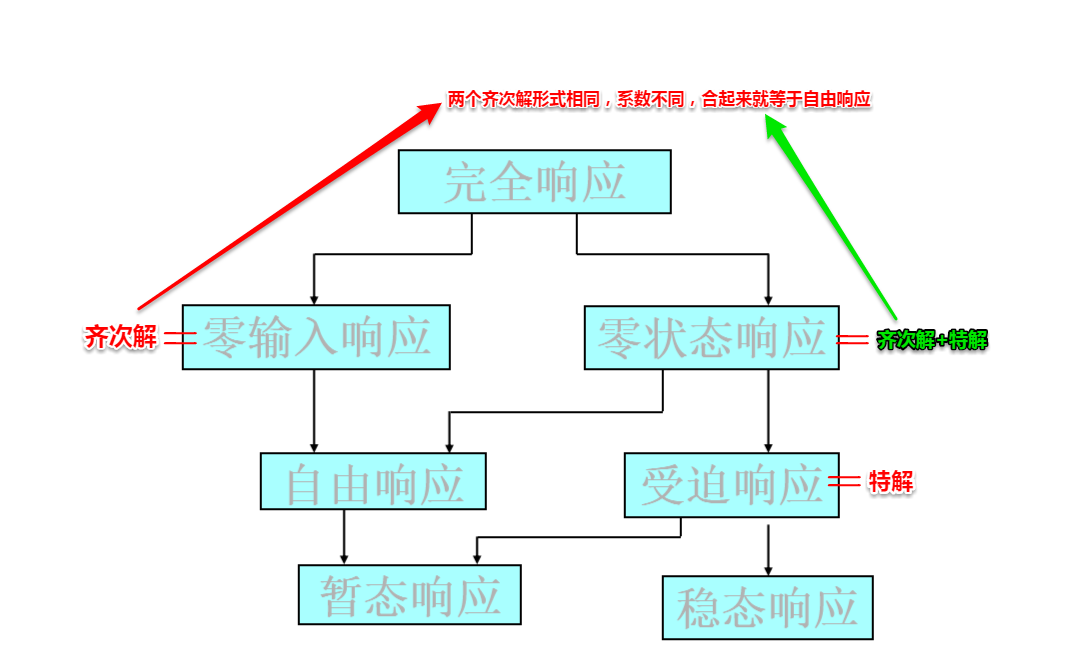
也即是:
完全响应(完全解)=齐次解+特解
=零输入响应+零状态响应
=自由响应+强迫响应
=暂态响应+稳态响应
公式关系解析
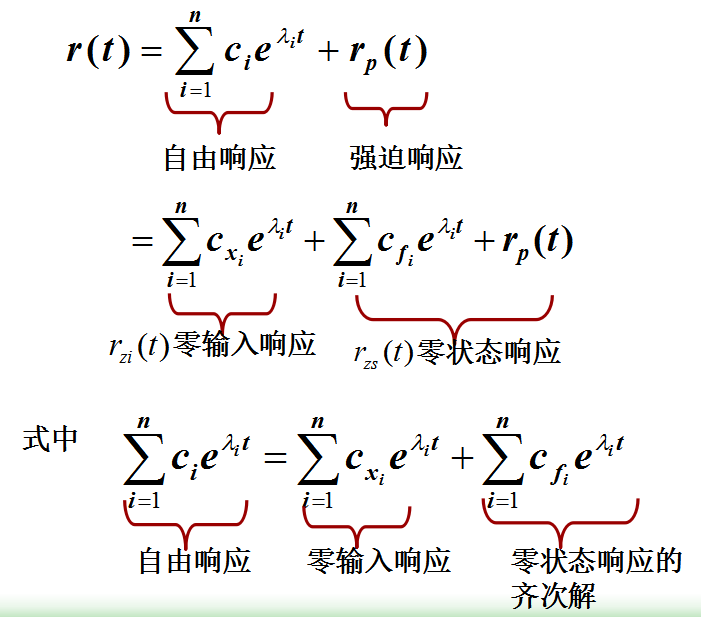
例题




