球盒问题

 

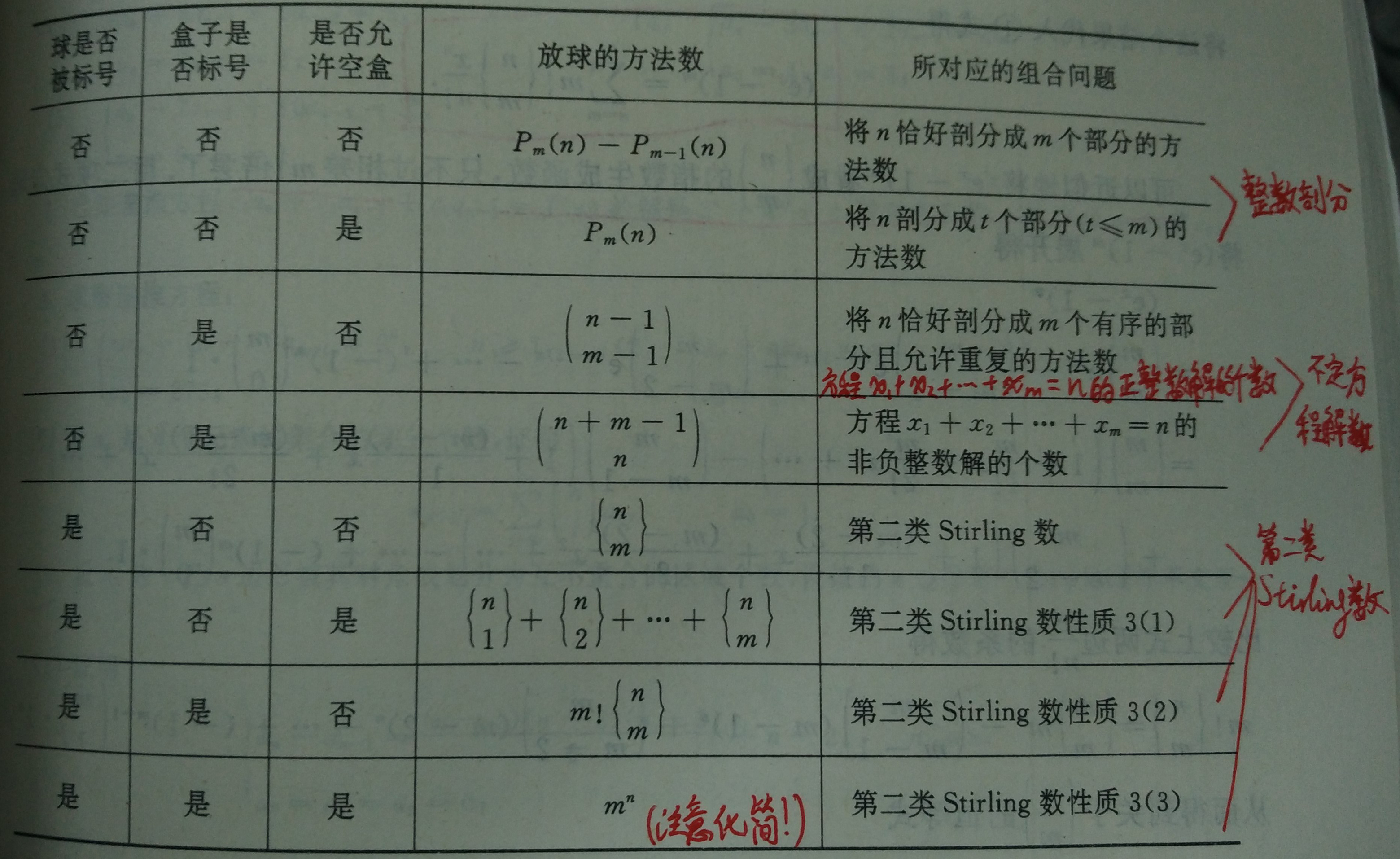
n相同球放入m个相同盒子，允许空盒的情况。这个问题和分拆函数（partition function）有关，似乎没有解析解。可以通过递归求解，代码为：

#include <iostream>

using namespace std;

int f(int n, int m)
{
if(m == 1 || n == 0) return 1;
if(m > n) return f(n, n);
return f(n, m-1) + f(n-m, m);
}

int main(){
int n,m;
while(true){
cin >> n >> m;
cout << f(n,m)<<endl;
}
return 0;
}

 

n个球放入n个盒子，n趋于无穷时，最多球的盒中球的个数为：

 

趣味题：一共有162个不同的小球，其中6个为红球，其余为白球。有6个不同的盒子。然后把这些小球平均分给这6个盒子。问：

（1）6个红球都在第一个盒子的概率？

（2）6个红球被分到同一个盒子的概率？

解：

（1）（156C21）/(162C27)

（2）1/（6^5）

第二小问模拟程序：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <cmath>
using namespace std;

int p[6];

int main(){
    srand(time(0));
    int n = 100000000, m=0;
    int t = n;
    while(t--){
        for (int i = 0 ; i < 6 ; i++){
            p[i] = 0;
        }
        for (int i = 0 ; i < 6 ; i++){
            p[rand()%6]++;
        }
        for (int i = 0 ; i < 6 ; i++){
            if (p[i] == 6){
                m++;
                break;
            }
        }
    }
    cout << m << "/"<< n << "="<<double(m)/double(n)<< " err="<<double(m)/double(n)-1/double(pow(6,5))<<endl;
    return 0; 
}