平衡二叉树-----失衡的情况

平衡二叉树---失衡情况

基本介绍

平衡二叉树也叫平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树， 可以保证查询效率较高。

具有以下特点：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

二叉树的四种不平衡情况

左左型LL

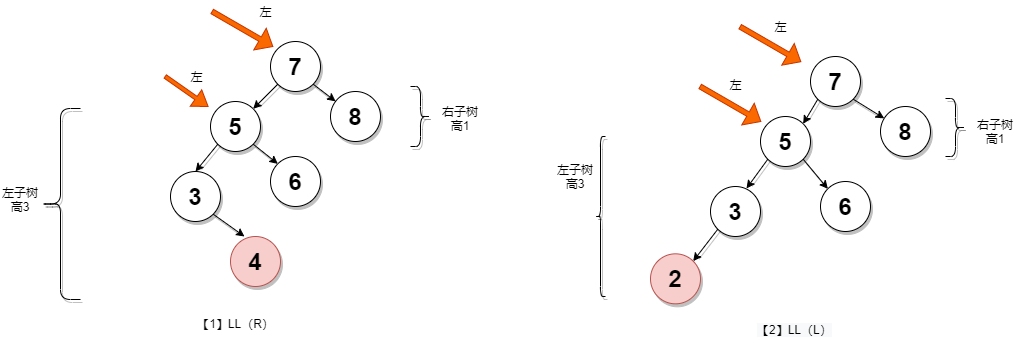
左右型LR

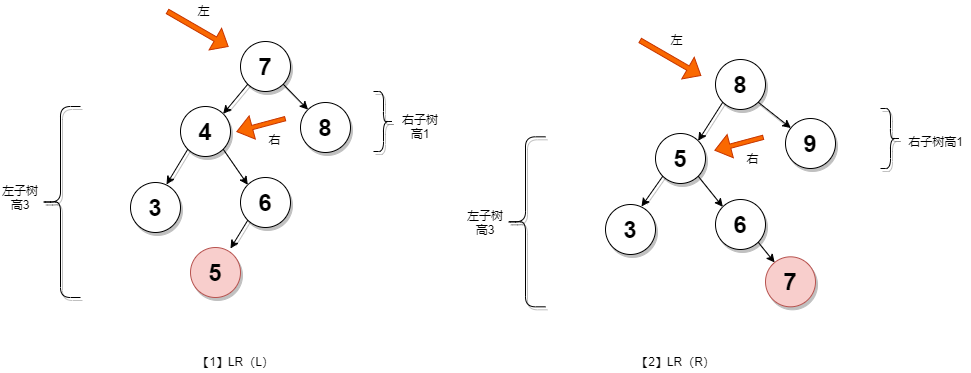
右左型RL

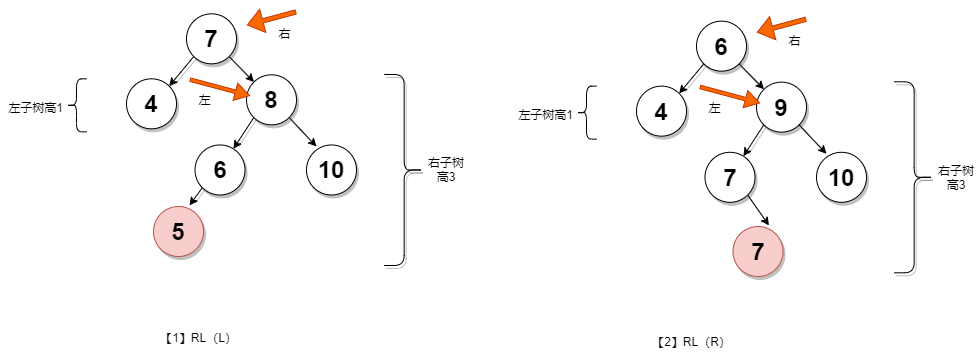
右右型RR

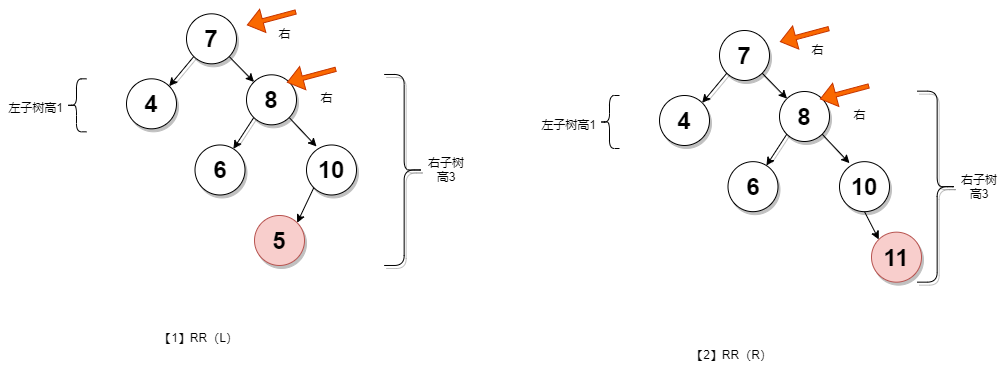
1.LL：称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

例如，在上面LL情况中，由于"根节点(7)的左子树(5)的左子树(3)还有非空子节点"，而"根节点(7)的右子树(8)没有子节点"；导致"根节点(7)的左子树(5)高度"比"根节点(7)的右子树(8·)"高2。

2.LR：称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。

例如，在上面LR情况中，由于"根节点(7)的左子树(4)的右子树(6)还有非空子节点"，而"根节点(7)的右子树8)没有子节点"；导致"根节点(7)的左子树(4)高度"比"根节点(7)的右子树(8)"高2。

3.RL：称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

例如，在上面RL情况中，由于"根节点(7)的右子树(8)的左子树(6)还有非空子节点"，而"根节点(7)的左子树(4)没有子节点"；导致"根节点(7)的右子树(8)高度"比"根节点(7)的左子树(4)"高2。

4.RR：称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

例如，在上面RR情况中，由于"根节点(7)的右子树(8)的右子树(10)还有非空子节点"，而"根节点(7)的左子树(4)没有子节点"；导致"根节点(7)的右子树(8)高度"比"根节点(7)的左子树(4)"高2。