05 Training versus Testing

 回顾上节内容：假设空间H有限，N足够大，不管A选择哪个h，Ein和Eout在一定范围内都是近似相等的，A根据D在H中挑选使得Ein足够小的g，就能说Ein=Eout(PAC)，即学习是可能的。

将学习分为两步：

train：A根据给定训练集D在H中选出g，使得E_in(g)≈0；

test：g在整个输入空间X上的表现要约等于在训练集D上的表现，使得E_out(g)≈E_in(g)。 

思考：①我们是否能保证Eout(g)≈Ein(g)；②是否能保证Ein(g)≈0？

①当M小时，根据霍夫丁不等式，坏事情发生的可能性很小，所以满足Eout(g)≈Ein(g)，但是M小，可供选择的h少，不一定能保证Ein(g)≈0。

②当M大时，根据霍夫丁不等式，坏事情发生的可能性不一定很小，所以不一定满足Eout(g)≈Ein(g)，但是M大，可供选择的h多，能保证Ein(g)≈0。

综上，应该选择适当大的M，不能过大或者过小。

前面已经解决了M有限的情况，下面解决无限大的M：

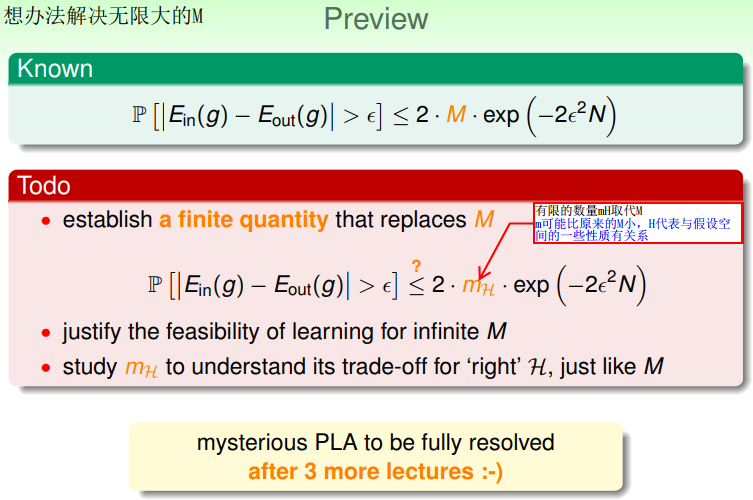
想办法找到有限值mH取代M：m表示可能比原来的M小，H代表与假设空间的一些性质有关系。

霍夫丁不等式本质是求并集，但是右边的式子2Mexp()是在默认无交集的情况下进行的，但是对于给定的D，在H中存在相似的h，这些h在D上的表现一致，即存在交集，所以2Mexp()作为上限来说过大了。将H中相似的h分为一类，将无限的|H|变为有限的类数dichotomies，每一个dichotomy在D上表现相同。

举例：感知机算法，考虑平面上的所有线

 

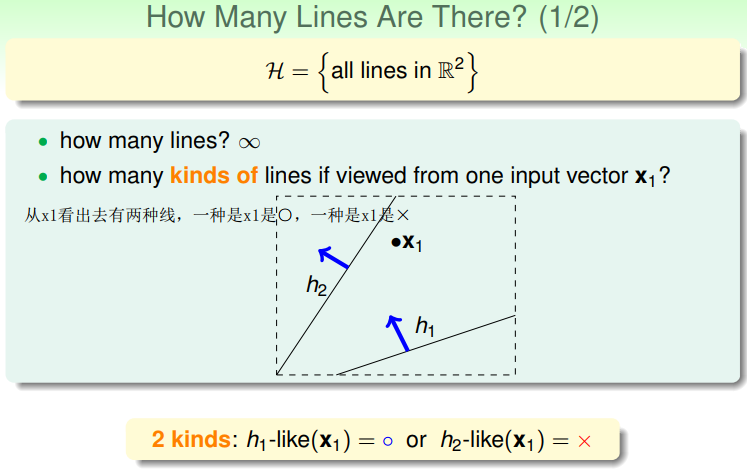
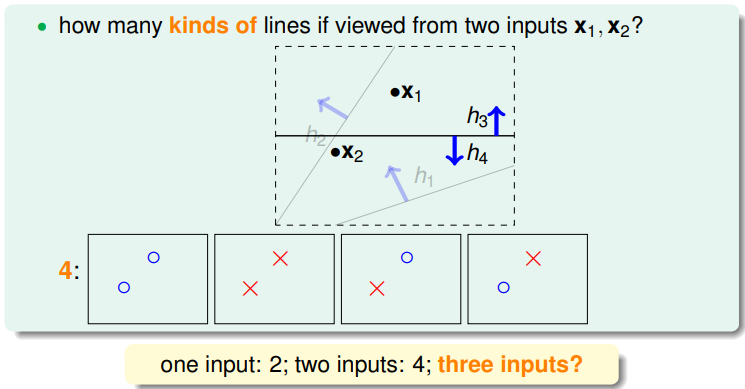
H是无限的，平面上有无数条直线，平面上有一个点x1，从x1看出去有两种线，一种是x1是○，一种是x1是×。平面上有两个点x1，x2，有四种类型的线，将D分为○○、○×、×○、××的h分别归为一类。

 

 

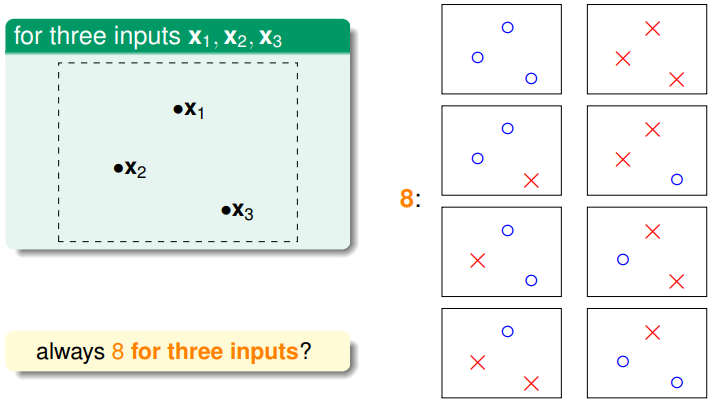
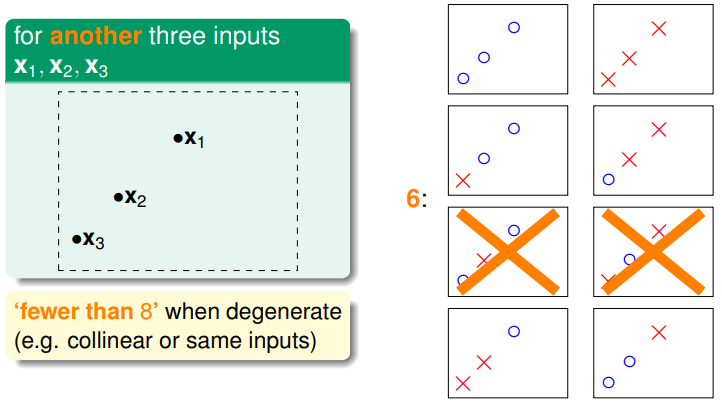
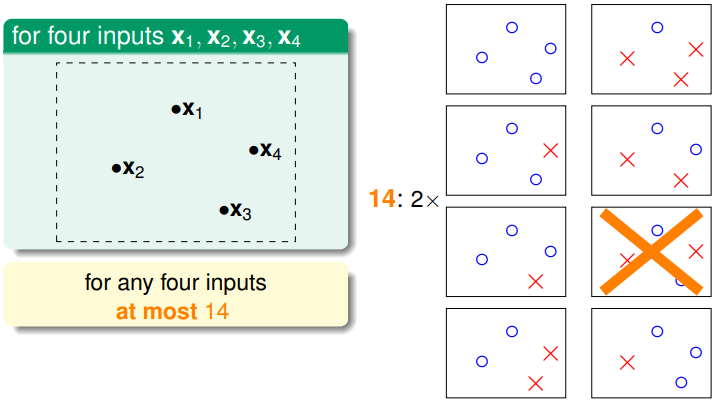
平面上有三个点时，根据点的分布不同，直线的类别也不同，可能是8类，也可能是6类（不超过2的N次方），所以dichotomies的数量是依赖于具体D（个数和分布）和H的，但是dichotomies的数量的最大值只依赖与D里样本点的个数N和H。

所以我们可以用类别最大值来代替M，该最大值是有限的并且远远小于2的N次方。

 

定义dichotomies的数量的最大值为N的成长函数，记为m_H(N)。------只和H、N有关。

即给定样本数N，H里假设类数是小于等于m_H(N)的。

对于2维感知机，m_H(1)=2，m_H(2)=4，m_H(3)=8，m_H(4)=14。

思考：如何计算成长函数？

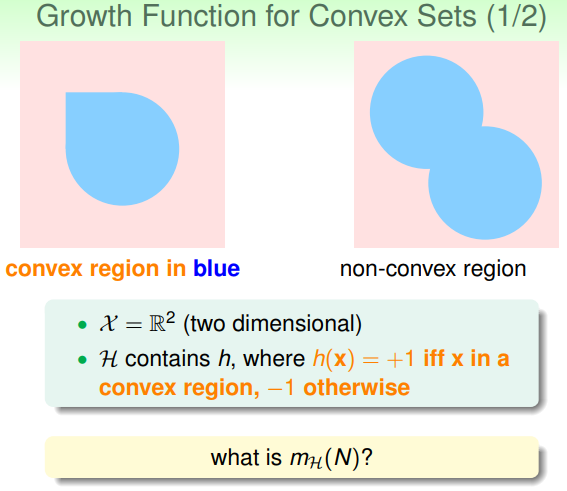
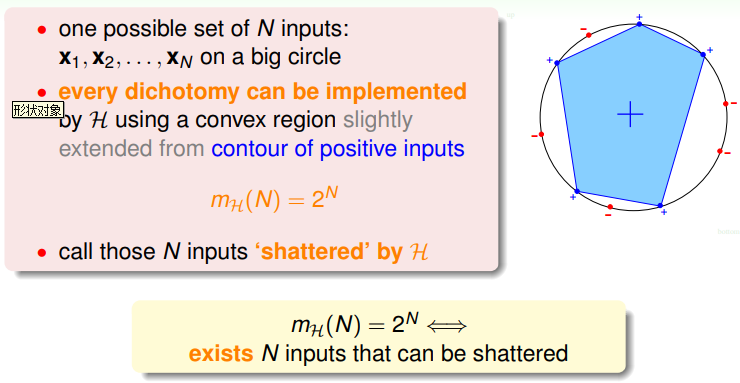
可以看出，成长函数可能是多项式形式的（好的），也可能是指数形式的（坏的），因为exp（）是指数减少的，多项式形式增加的比指数减少的慢，能保证最终右式2Mexp()趋于0，所以多项式型的成长函数能保证坏事情发生的可能性很小，但是指数型的不一定。 

shatter：如果H里的假设能够保证k个输入能够输出任意标签的组合，称H能shatter这k个输入。 

break point k：H不能shatter这k个输入，称k为断点。

 

思考：break point和成长速度有关系吗？成长速度=N的(k-1)次方？

猜想，只要存在断点，就能保证成长函数是多项式型，进而保证了test。