数论 —— 质数 + 欧拉函数
简单定理
- 若 \(a\) 是自身模素数 \(p\) 的逆,当且仅当 \(a \equiv 1\pmod{p}\) 或 \(a \equiv -1\pmod{p}\)
威尔逊定理
对于一个素数 \(p\) 有 \((p-1)! \equiv -1\pmod{p}\),即 \((p-1)! \equiv p-1\pmod{p}\)
证明

同时存在逆定理,若 \(n\) 为大于等于 \(2\) 的正整数且 \((n-1)! \equiv -1\pmod{n}\) 则 \(n\) 为素数。
证明

费马小定理
对于一个素数 \(p\) 和一个正整数 \(a\) 满足 \(p \nmid a\)(\(a\) 不能被 \(p\) 整除),则 \(a^{p-1} \equiv 1\pmod{p}\)
证明


对于一个素数 \(p\) 和一个正整数 \(a\),则 \(a^{p} \equiv a\pmod{p}\)
证明
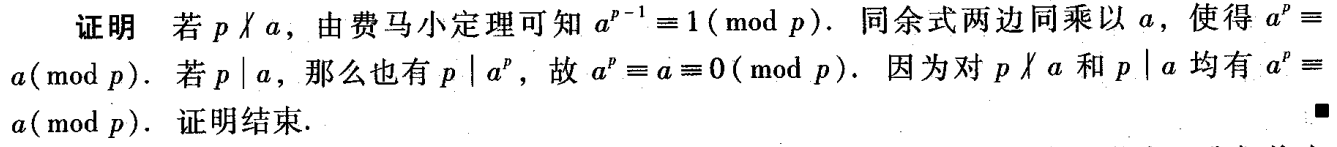
通过简单的变化还可以得到这些定理:
- 对于一个素数 \(p\) 和一个正整数 \(a\) 满足 \(p \nmid a\)(\(a\) 不能被 \(p\) 整除),则 \(a^{p-2}\) 是 \(a\) 模 \(p\) 的逆
- 对于一个素数 \(p\) 和两个个正整数 \(a,b\) 满足 \(p \nmid a\)(\(a\) 不能被 \(p\) 整除),对于同余线性方程 \(ax \equiv b\pmod{p}\) 的解 \(x\) 满足 \(x \equiv a^{p-2}b\pmod{p}\)。
伪素数+卡迈克尔数+米勒检验
通过费马小定理可知:对于一个整数 \(n\),若有任何一个整数 \(b\) 满足 \(b^{n} \not\equiv b\pmod{n}\) 则 \(n\) 为合数。
伪素数定义:令 \(b\) 为正整数。若 \(n\) 是正合数且满足 \(b^{n} \equiv b\pmod{n}\),则称 \(n\) 为以 \(b\) 为基的伪素数。
卡迈克尔数定义:若一个合数 \(n\) 对于所有满足 \(\gcd(d,n) = 1\) 的正整数 \(b\) 都有 \(b^{n-1} \equiv 1\pmod{n}\),则 \(n\) 为卡迈克尔数,或者可以称其为绝对伪素数。
接下来就是米勒检验了:
- 其中 \(n\) 为奇数,设 \(b^{n-1} \equiv 1\pmod{n}\)
- 设 \(x = b^{\frac{n-1}{2}}\) 可得 \(x^2=b^{n-1}\equiv 1 \pmod{n}\)
- 根据简单定理中的第一条,若 \(n\) 为素数,则必定满足 \(x\equiv\pm 1 \pmod{n}\),反之则 \(n\) 为合数
米勒检验定义:令正整数 \(n\) 满足 \(n > 2\) 且 \(n-1=2^st\),其中 \(s\) 为非负整数,\(t\) 为奇正整数。其中 \(j\) 满足 \(1 \le j \le s-1\),若有一个 \(j\) 满足 \(b^{2^jt}\equiv-1 \pmod{n}\) 或 \(b^{t}\equiv1 \pmod{n}\),则称 \(n\) 通过了以 \(b\) 为基的米勒检验。
概率验证素数法
有一条关于米勒检验的定理:
- 若 \(n\) 为奇正合数,则最多有 \(\frac{n-1}{4}\) 个 \(b(1 \le b \le n-1)\) 可以使 \(n\) 通过米勒检验。
也就是至少 \(\frac{3(n-1)}{4}\) 个 \(b\) 可以验证出 \(n\) 为合数。
考虑随机一个 \(b\),若 \(n\) 为合数,则有 \(\frac{1}{4}\) 的概率检查出 \(n\) 是合数。
我们只用随机 \(20\) 个 \(b\),极大的概率可以检查出 \(n\) 是否为合数。
点击查看代码
LL qpow(LL A, LL B, LL mod){ LL ret = 1; // 快速幂
while(B > 0){
if(B & 1) ret = ret * A % mod;
A = A * A % mod, B >>= 1;
}
return ret;
}
mt19937_64 rnd(time(0));// 可改变里面的种子
struct Miller_Rabin{ // 米勒验证质数
int round = 60; // 随机验证的次数
bool check(LL n){ // 1 表示是质数
if(n == 2 || n == 3) return 1;
if(n == 1 || n % 2 == 0) return 0;
LL d = n - 1, cnt = 0;
while(d % 2 == 0) cnt++, d >>= 1;
for(int RR = 1; RR <= round; RR++){
LL b = rnd() % (n - 3) + 2, Pow = qpow(b, d, n);
if(Pow == 1) continue;
for(int _cnt = cnt - 1; _cnt >= 0; _cnt--){
if(Pow == n - 1) break;
Pow = Pow * Pow % n;
if(_cnt == 0) return 0;
}
}
return 1;
}
}mr;
欧拉定理
- \(\varphi(n)\) 或 \(\phi(n)\) 表示小于等于 \(n\) 且与 \(n\) 互质的个数。
- 模 \(n\) 的既约剩余系是由 \(\varphi(n)\) 个数构成的集合,集合中的数都与 \(n\) 互质,且模 \(n\) 后都不同
欧拉定理:对于正整数 \(m\),且 \(a\) 是一个整数满足 \(\gcd(a,m) = 1\),则 \(a^{\varphi(m)} \equiv 1\pmod{m}\)
证明

欧拉函数性质
- 将 \(n\) 质因数分解得 \(n = p_1^{c_1}p_2^{c_2}p_3^{c_3}\cdots p_s^{c_s}\),则 \(\varphi(n) = \varphi(p_1^{c_1})\varphi(p_2^{c_2})\varphi(p_3^{c_3})\cdots \varphi(p_s^{c_s})\)
证明

- 对于两个整数 \(m\) 和 \(n\) 满足 \(\gcd(n, m) = 1\),则 \(\varphi(nm) = \varphi(n)\varphi(m)\)
证明

-
若 \(p\) 为素数,则 \(\varphi(p) = p - 1\)。同时存在逆定理,即若 \(\varphi(p) = p - 1\),则 \(p\) 为素数。
-
若 \(p\) 为素数,则 \(\varphi(p^a) = p^a - p^{a-1}\)。
-
将 \(n\) 质因数分解得 \(n = p_1^{c_1}p_2^{c_2}p_3^{c_3}\cdots p_s^{c_s}\),则 \(\varphi(n) = n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots (1-\frac{1}{p_s})\)
证明

-
若 \(n\) 为大于 \(2\) 的整数,则 \(\varphi(n)\) 为偶数
-
将 \(n\) 质因数分解,\(\varphi(n) = \prod_{i=1}^{s}{p_i^{c_j - 1}(p_i - 1)}\)
-
\(\sum_{d|n}{\varphi(d)} = n\)
证明

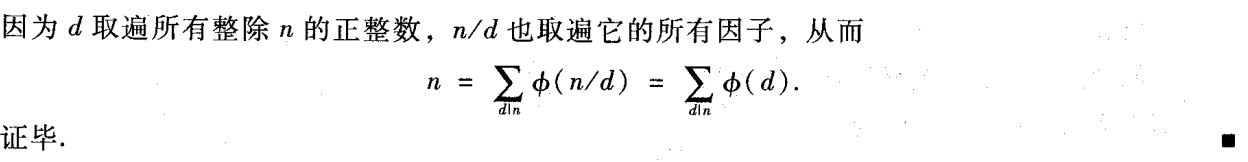
- \(\varphi(\varphi(n)) \le \frac{n}{2}\)
证明

两种方法求解欧拉函数
时间复杂度 \(O(\sqrt{n})\)
LL F(LL n){
LL ret = n;
for(LL i = 2; i * i <= n; i++){
if(n % i == 0) ret = ret / i * (i - 1);
while(n % i == 0) n /= i;
}
if(n > 1) ret = ret / n * (n - 1);
return ret;
}
LL F(LL n){
LL ret = 1;
for(LL i = 2; i * i <= n; i++){
bool ooo = (n % i == 0);
while(n % i == 0) n /= i, ret = ret * i;
if(ooo) ret = ret / i * (i - 1);
}
if(n > 1) ret = ret * (n - 1);
return ret;
}
拓展欧拉定理
https://oi-wiki.org/math/number-theory/fermat/#扩展欧拉定理
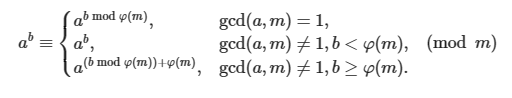
其实就是对于显然第三种情况可以求解第一种情况,所以实现的时候没有必要判断 gcd,但是注意需要特别判断第二种情况。
证明

应用
对于降幂,通常是直接 \(a^b \bmod m = a^{b \bmod \varphi(m)+\varphi(m)} \bmod m\)
练习:https://www.luogu.com.cn/problem/P4139
练习:https://www.luogu.com.cn/problem/CF906D



