拓扑排序

来自XXX大巨佬

一. 拓扑排序简介

1. 拓扑排序的定义

给定一个 \(n\) 个点 \(m\) 条边的有向无环图，对于每对边 \((u, v)\)， \(u\) 在排序后的序列里必须在 \(v\) 的前面，这样的排序就叫拓扑排序。
拓扑排序也是一种排序，就是为求拓扑序。
a

2. 拓扑排序的思想

• 每次取出一个入度为 0 的点，断掉它的所有出边，循环往复，直到所有元素都被取出，这个取出的过程就是拓扑排序。

• 若没有取出所有元素，又没有入度为 0 的点，就说明有环。

3. 怎么写拓扑排序

逐月P1360 拓扑排序1(模板)

• 拓扑排序取出来的点这会影响它所到达的点，所以只用查看这些点即可，这里以上方的模板题为例题。

• 所以因为第一点，无论以下哪种写法，都是 \(n\) 个状态， \(m\) 次转移，时间复杂度均为 \(O(n + m)\)，只是常数不同。

(1)：类广搜

每次取出任意一个入度为 0 的点，在断边，把新的入度为 0 的点记录下来，既可以用栈，也可以用队列实现，这里两种写法都贴一下。

栈版本

const int MAXN = 1e5 + 5;

vector<int> g[MAXN];
int n, m, x, y, top, c[MAXN], stk[MAXN]; //c 数组判断入度是否为 0

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> x >> y;
    g[x].push_back(y), c[y]++;
  }
  for(int i = 1; i <= n; i++){ //把最开始入度为 0 的点压入栈
    if(!c[i]){
      stk[++top] = i;
    }
  }
  while(top){
    int u = stk[top--];
    for(int i : g[u]){ 
      c[i]--;      //断开栈顶连出去的边
      if(!c[i]){   //检查有没有入度为 0 的点
        stk[++top] = i;  //压入栈
      }
    }
    cout << u << ' ';
  }
  return 0;
}

队列版本

const int MAXN = 1e5 + 5;

vector<int> g[MAXN];
int n, m, x, y, h = 1, t, c[MAXN], que[MAXN]; 

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> x >> y;
    g[x].push_back(y), c[y]++;
  }
  for(int i = 1; i <= n; i++){
    if(!c[i]){
      que[++t] = i;
    }
  }
  while(h <= t){
    int u = que[h++];
    for(int i : g[u]){
      c[i]--;
      if(!c[i]){
        que[++t] = i;
      }
    }
    cout << u << ' ';
  }
  return 0;
}

(2). 分治（记忆化搜索）

核心就是把大问题化成若干个小问题，再解决大问题。每个点先求出它所有连出的点 \(x\) 和 \(x\) 后面的拓扑序，再把当前点放到最前面。因可能不是连通图，需要枚举每个点进行分治，可用栈和双端队列做，这里挂一下栈版本。

const int MAXN = 1e5 + 5;

bool v[MAXN];
vector<int> g[MAXN];
int n, m, x, y, top, stk[MAXN];

void Dfs(int x){
  if(v[x]){  //有重复元素
    return ;
  }
  v[x] = 1;
  for(int i : g[x]){
    Dfs(i); //求出连到的点的拓扑序
  }
  stk[++top] = x;  //把当前点压到栈顶
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> x >> y;
    g[x].push_back(y);
  }
  for(int i = 1; i <= n; i++){
    Dfs(i);
  }
  while(top){
    cout << stk[top--] << ' ';
  }
  return 0;
}

(3). 深搜

枚举所有点，若它的入度为 0 且没有在拓扑序中，把它进行转移，断边，若它连出的点入度为 0 且没有在拓扑序里，转移到连出的点。本质与第一种一样。

const int MAXN = 1e5 + 5;

bool v[MAXN];
vector<int> g[MAXN];
int n, m, x, y, top, c[MAXN], stk[MAXN];

void Dfs(int x){
  // 因为只有可能为最开始的入度为 0 的那个点重复导致当前点重复，所以无需在这写标记
  cout << x << ' ';
  for(int i : g[x]){
    c[i]--;  // 去边
    if(!c[i]){  //入度为 0
      v[i] = 1;  // 标记出现过
      Dfs(i);
    }
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> x >> y;
    g[x].push_back(y), c[y]++;
  }
  for(int i = 1; i <= n; i++){
    if(!c[i] && !v[i]){   // 入度为 0 且没有在拓扑序中
      Dfs(i);
    }
  }
  return 0;
}

(4). 建反图

把边反过来，再做和 (3) 相同的操作，一般不使用，只在正图不能做或麻烦才建反图，了解一下即可。

注意：(2) ~ (4) 不能求最小字典序拓扑序，第一种把栈或队列改为优先队列即可，有 hack 数据 ： 1 -> 3, 2 -> 4 ，应输出 1 2 3 4，而深搜会输出 1 3 2 4。

4. 拓扑排序的用处

对于一些算法，如 \(dp...\), 需要无后效性（也就是拓扑序），但是不知道拓扑序是什么，又是有向无环图，就可以有拓扑排序求出拓扑序，再去完成接下来的任务。还有一种作用，就是判环，就是看是不是所有点都取出来了。

拓扑序的实际应用

题目1：洛谷P4017 最大食物链计数

题意

• 给你一个 \(n\) 个动物和有 \(m\) 条关系式的食物网，问这个食物网中最大食物链的数量。这里的“最大食物链”是即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者， 答案对 80112002 取模。

• \(1 \le n \le 5000, 1 \le m \le 500000\)

思路

• 首先可以暴搜，搜出所有食物链，但是肯定会超时。

• 首先建图，这很显而易见，被吃的动物 \(x\) 向所有吃动物 \(x\) 的动物连边。

• 令 \(cnt[x]\) 终点为 \(x\) 的方案数，那么 \(cnt[x] = \sum\limits_{(y, x) \in E}{cnt[y]}\)，所以要先求出所有 \(cnt[y]\)。

• 如果考虑 \(dp\)， 这就可以用拓扑排序求拓扑序了，对于所有边 \((x, y)\)，在排列里满足 \(x\) 在 \(y\) 前面。

• 接下来就是一个模板 \(dp\)，也可以在拓扑排序里就求出来，贴一个代码。

const int MAXN = 5010, INF = 80112002;

vector<int> g[MAXN];
int n, m,  x, y, h = 1, t, ans, que[MAXN], c[MAXN], cnt[MAXN];

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> x >> y;
    g[x].push_back(y), c[y]++;
  }
  for(int i = 1; i <= n; i++){
    if(!c[i]){
      que[++t] = i, cnt[i] = 1;
    }
  }
  while(h <= t){  // 拓扑排序
    int u = que[h++];
    for(int i : g[u]){
      c[i]--, cnt[i] = (cnt[i] + cnt[u]) % INF;  // 断边，求方案数
      if(!c[i]){
        que[++t] = i;
      }
    }
  }
  for(int i = 1; i <= n; i++){  // 统计答案
    ans = (ans + (g[i].size() == 0) * cnt[i]) % INF;
  }
  cout << ans;
  return 0;
}

• 时间复杂度：拓扑排序 \(O(n + m)\)，\(dp\)每个点和边都枚举一次\(O(n + m)\)，总时间复杂度：\(O(n + m)\)。

题目2：洛谷P1685 游览

题意

• 给定一个 \(n\) 个点 \(m\) 条边的有向无环图，第 \(i\) 条边是从 \(x[i] -> y[i]\) ，走第 \(i\) 条边需要花 \(t[i]\) 时间，现在要把 \(s\) 到 \(e\) 的所有不同的路走一遍。 并且从每条路走完需要花 \(t_0\) 时间回到 \(s\)（最后一条就不需要了）。

• $ 1 \le n \le 10^4, 1 \le m \le 5 \times 10 ^ 4$，答案需对 10000 取模。

思路

• 一个暴力思路：把每条路线都搜一遍，这样一定会超时。

• 我们先来分析一下：首先从 \(e\) 回 \(s\) 的时间 \(=\) 从 \(s\) 到 \(e\) 的路线数 \(\times t_0\)。那么我们可以推出一定需要记录从 \(s\) 到所有点的路线数，否则没法做，所以令 \(cnt[i]\) 为 \(s\) 到 \(i\) 的路线数，最开始只有 \(cnt[s] = 1\)。

• 接下来有两种思路，请大家一个个看。

思路1

• 我们做一下思想转换，若不算从 \(e\) 回到 \(s\) 的时间，答案 \(=\sum\limits_{所有路线}{每条路线所花的时间} = \sum\limits_{1 \le i \le m}{t[i] \times 第 i 条边走过的次数}\)，（此处写得比较不严谨，请见谅，严谨的话要写太多）。

• 所以我么只需要求出每条边经过的次数在注意一下取模细节就行了，接下来的问题就是求每条边经过的次数。其实这个很简单，第 \(i\) 条边经过的次数 $ = s$ 到 \(x[i]\) 的线路数（也就是 \(cnt[x[i]]\)）\(\times t\) 到 \(e\) 的路线数。

• 所以我们重新定义一下：令 \(cnt[0][x], cnt[1][x]\) 分别为 \(s\) 到 \(x\) 的路线数和 \(x\) 到 \(e\) 的路线数，最开始 \(cnt[0][s] = cnt[1][e] = 1\) 则第 \(i\) 条边需经过 \(cnt[0][x[i]] \times cnt[1][y[i]]\) 次，所以这道题的答案就是 ：\(\sum\limits{1 \le i \le m}{cnt[0][x[i]] \times cnt[1][y[i]] \times t[i]}\) \(+ (cnt[0][e] - 1) \times t_0\)

• 补充一下：\(cnt[0][x]\) 可以用拓扑排序后 \(dp\)，\(cnt[1][x]\) 可以建反图再做一遍拓扑排序后 \(dp\)，当然也可以记忆化搜索，再注意一下取模的细节即可，两边拓扑排序可以用一个函数完成。

• 时间复杂度：两遍拓扑排序：\(O(n + m)\);

const int MAXN = 1e4 + 5, Mod = 1e4;

vector<int> g[2][MAXN];  //正反图
int n, m, ans, sx, ex, x, y, w, ti;
int deg[2][MAXN], cnt[2][MAXN];

struct Edge{
  int x, y, w;
}e[5 * MAXN];

void Bfs(bool v){  //是记录从 s 到 x 的方案数还是记录从 x 到 e 的方案数，从而进行拓扑排序
  queue<int> que;
  for(int i = 1; i <= n; i++){
    if(!deg[v][i]){
      que.push(i);
    }
  }
  while(!que.empty()){
    int u = que.front();
    que.pop();
    for(int i : g[v][u]){
      deg[v][i]--;
      cnt[v][i] = (cnt[v][i] + cnt[v][u]) % Mod;
      if(!deg[v][i]){
        que.push(i);
      }
    }
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m >> sx >> ex >> ti;
  for(int i = 1; i <= m; i++){
    cin >> e[i].x >> e[i].y >> e[i].w;
    deg[0][e[i].y]++, deg[1][e[i].x]++;
    g[0][e[i].x].push_back(e[i].y), g[1] [e[i].y].push_back(e[i].x); //建正反图
  }
  cnt[0][sx] = 1, cnt[1][ex] = 1, Bfs(0), Bfs(1);
  for(int i = 1; i <= m; i++){
    ans = (ans + cnt[0][e[i].x] * cnt[1][e[i].y] % Mod * e[i].w) % Mod;  //统计答案
  }
  cout << (ans + (cnt[0][ex] - 1) * ti) % Mod;
  return 0;
}

思路2

• 直接用纯递推做，令 \(sum[x]\) 为从 \(s\) 到 \(x\) 所有路径的总消耗时间，则 \(sum[y] = \sum\limits_{1 \le i \le m, y[i] = y}{sum[x[i]] + cnt[x[i]] * t[i]}, cnt[y] = \sum\limits_{1 \le i \le m, y[i] = y}{cnt[x[i]]}\) ，这个过程 \(dp\)，所以可用拓扑排序求拓扑序，边做排序边 \(dp\)。 那么答案就是 \(sum[e]\)。

• 时间复杂度：拓扑排序：\(O(n + m)\)。

const int MAXN = 1e4 + 5, Mod = 1e4;

struct Edge{
  int x, w;
};

vector<Edge> g[MAXN];
bool v[MAXN];
int n, m, s, e, x, y, w, ti;
int deg[MAXN], cnt[MAXN], sum[MAXN];

void Dfs(int x){  // 拓扑排序
  v[x] = 1;
  for(Edge i : g[x]){
    deg[i.x]--, cnt[i.x] = (cnt[i.x] + cnt[x]) % Mod;
    sum[i.x] = (sum[i.x] + sum[x] + cnt[x] * i.w) % Mod;
    if(!deg[i.x]){
      Dfs(i.x);
    }
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m >> s >> e >> ti;
  for(int i = 1; i <= m; i++){
    cin >> x >> y >> w;
    g[x].push_back({y, w}), deg[y]++;
  }
  cnt[s] = 1, Dfs(s);
  for(int i = 1; i <= n; i++){
    if(!deg[i] && i != s && !v[i]){
      Dfs(i);
    }
  }
  cout << (sum[e] + (cnt[e] + Mod - 1) *  ti) % Mod;
  return 0;
}

注意：两种方法都需先把所有入度为 0 的点和 \(s\) 丢进队列，不然有些状态永远不能入队。

题目3：洛谷P1983 车站分级

题意

• 有 \(n\) 个站台 \(m\) 趟列车，每个站台有一个级别（级别必须 \(> 0\)），第 \(i\) 趟停靠了 \(s[i]\) 个站台，按照顺序给出，每一趟都满足如下要求：如果这趟车次停靠了火车站 \(x\)，则始发站、终点站之间所有级别大于等于火车站 \(x\) 的都必须停靠。

• \(1 \le n, m \le 1000\)。

思路

• 根据题意，那么所有第 \(i\) 趟停靠的站台的等级都大于起始站至终点站所有没被停靠的站台的等级。所以可以把每一个站台看做点，对于每个趟列车，把起始站至终点站所有没被停靠的站台向停靠的站台连一条有向边，表示小于关系，这个图就是一个的有向无环图，当然可能有重边。

• 令 \(c[i]\) 为 第 \(i\) 个站台的等级至少为多少，则 \(c[i] = \max\{c[j] + 1\}\)，然后就可以进行拓扑排序 \(+dp\)，这道题就完成了。

• 难道你真以为这道题就这样写完了，如果真写完就不必放这里了。我们算一下时间复杂度，每趟列车最多可能建 \(n \times n \div 4\) 条边，共 \(m\) 趟，拓扑排序：\(O(n + m)\)，总时间复杂度：\(O(n^2 \times m)\)，就肯定超时了。

• 所以我们需优化建图方式，来看一下刚刚的建图方式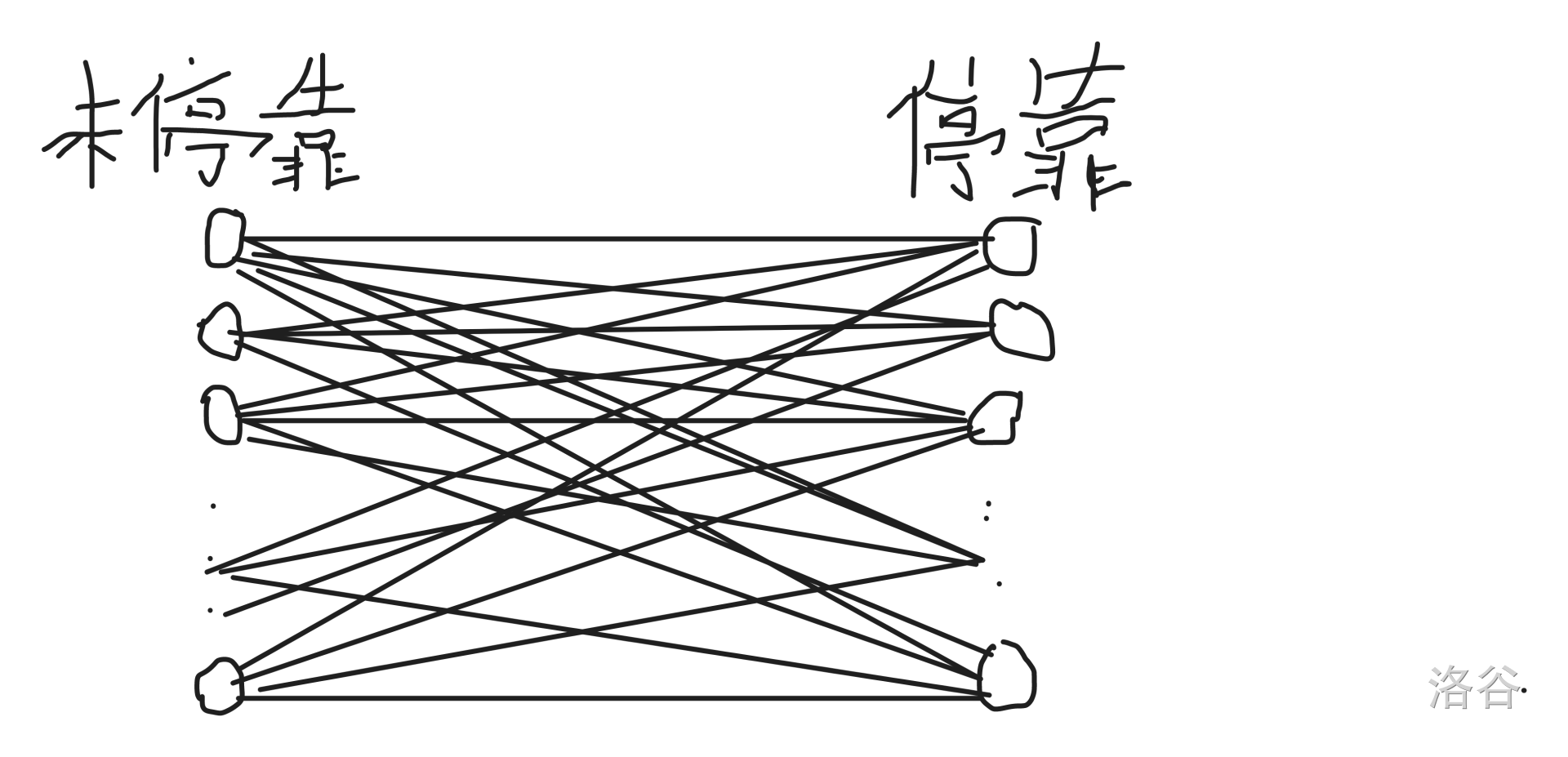：（忘画箭头了，理解是未停靠的站台指向停靠的站台就行）

• 两个集合中每两个点建一条边，太浪费，就可以每次构造虚拟点，把两个集合中的点都和虚拟点相连即可，一边边权为 0 ，一边边权为 1，看一下现在的建图方式效果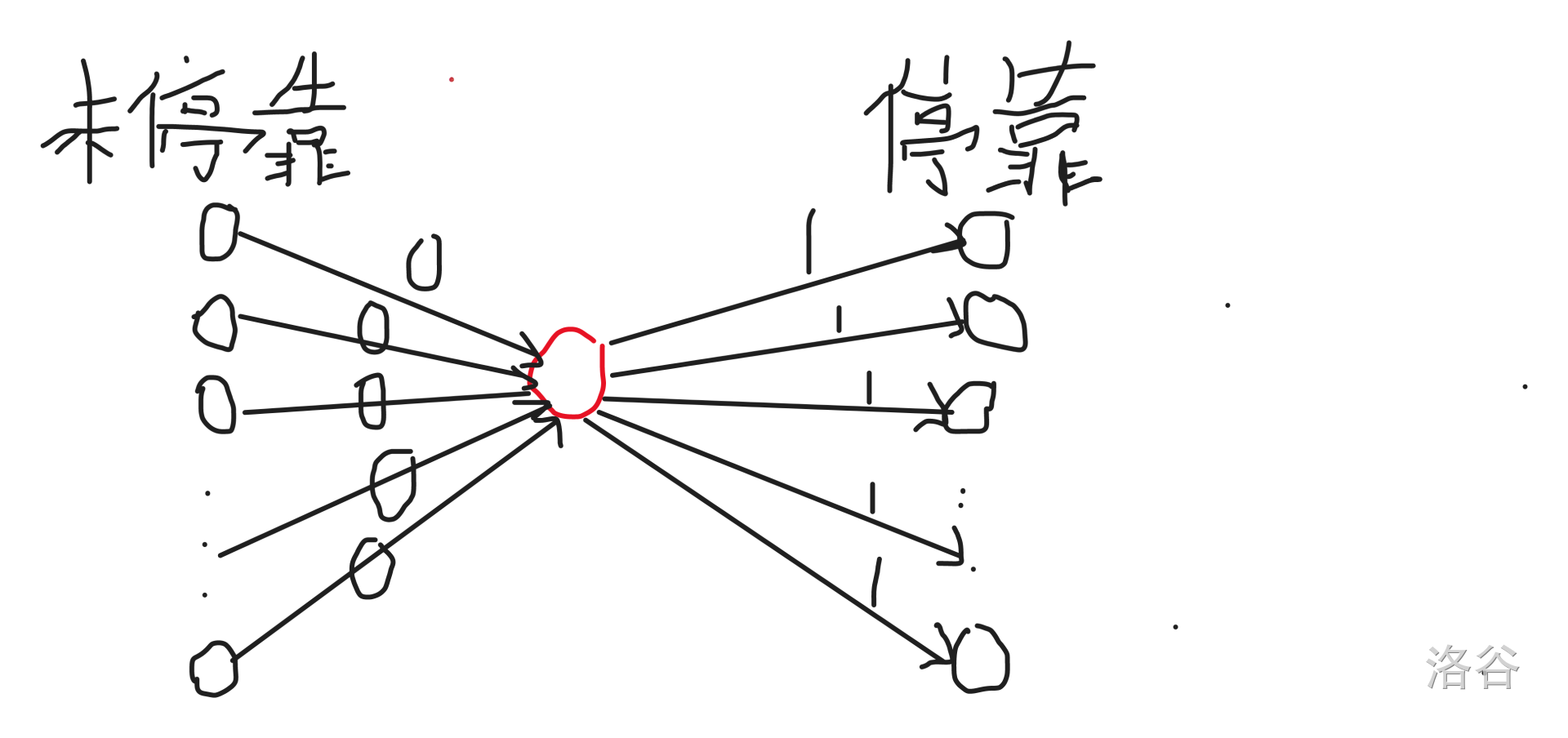：（红色的为虚拟点）。

• 那么 \(c[i] = \max\limits_{(j, i, w) \in E}\{c[j] + w\}\) ，\(w\) 为这条边的边权，最后把每个站台的等级取最大值。

• 分析一下时间复杂度，每次最多建 \(n\) 条边，一个虚拟点，共 \(m\) 趟，\(n + m\) 个点，\(n \times m\)条边，这里花 \(O(n \times m)\) 的时间复杂度，拓扑排序：\(O((n + m) + n \times m) = O(n \times m)\)，总时间复杂度：\(O(n \times m)\)。

const int MAXN = 1005;

struct Edge{ //边
  int x;
  bool v;
};

// 因为有虚拟点，所以数组要开大一点

bool v[MAXN];
vector<Edge> g[MAXN * 2];
int n, m, k, ans, h = 1, t, que[MAXN * 2], a[MAXN], deg[MAXN * 2], c[MAXN * 2];

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= m; i++){
    cin >> k;
    for(int j = 1; j <= k; j++){
      cin >> a[j];
      v[a[j]] = 1, g[n + i].push_back({a[j], 0}), deg[a[j]]++;  //虚拟点和停靠站建边
    }
    for(int j = a[1]; j <= a[k]; j++){ 
      if(!v[j]){
        g[j].push_back({n + i, 1}), deg[n + i]++;  //未停靠的站和虚拟建边
      }
    }
    fill(v + 1, v + n + 1, 0);
  }
  // 拓扑排序
  for(int i = 1; i <= n + m; i++){
    if(!deg[i]){
      que[++t] = i, c[i] = 1;
    }
  }
  while(h <= t){
    int u = que[h++];
    for(Edge i : g[u]){
      deg[i.x]--, c[i.x] = max(c[i.x], c[u] + i.v); 
      if(!deg[i.x]){
        que[++t] = i.x;
      }
    }
  }
  for(int i = 1; i <= n + m; i++){  // 统计答案
    ans = max(ans, c[i]);
  }
  cout << ans;
  return 0;
}