题目描述
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
题目地址
思路
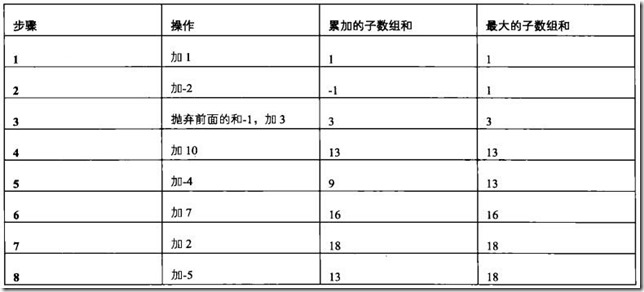
数组分析:下图是我们计算数组(1,-2,3,10,-4,7,2,-5)中子数组的最大和的过程。通过分析我们发现,累加的子数组和,如果大于零,那么我们继续累加就行;否则,则需要剔除原来的累加和重新开始。
过程如下:
Python
# -*- coding:utf-8 -*- class Solution: def FindGreatestSumOfSubArray(self, array): # write code here if not array: return 0 maxSum = array[0] tempSum = 0 for x in array: tempSum += x if tempSum > maxSum: maxSum = tempSum if tempSum < 0: tempSum = 0 return maxSum if __name__ == '__main__': result = Solution().FindGreatestSumOfSubArray([2,8,1,5,9]) print(result)
作者:huangqiancun
出处:http://www.cnblogs.com/huangqiancun/
本博客若无特殊说明则由作者原创发布,欢迎转载,但请注明出处 :)