题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
题目地址
思路
思路:
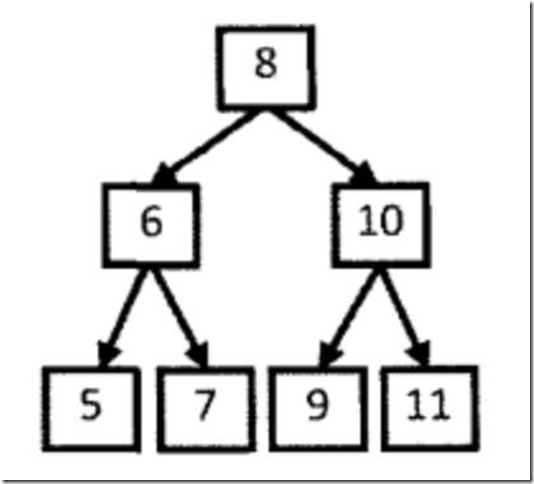
以[5,7,6,9,11,10,8]为例,后序遍历结果的最后一个数字8 就是根结点的值,在这个数组中,前三个数字5、7和6都比8小,是值为8的结点的左子树结点;后三个数字9、11和10都比8大,是值为8的结点的右子树。
用同样的方法确定与数组每一部分对应的子树的结构,这其实就是一个递归的过程,对于序列5,7,6,最后一个数字6是左子树的根结点的值,数字5比6小,是值为6的结点的左子结点,而7则是它的右子结点。同样,在序列9、11、10中,最后一个数字10是右子树的根结点,数字9比10小,是值为10的结点的左子结点,而11则是它的右子结点。
使用递归的方法,先判断数组的左子树和右子树的位置,找出左子树后。判断右子树是不是二叉搜索树。
Python
# -*- coding:utf-8 -*- class Solution: def VerifySquenceOfBST(self, sequence): # write code here if len(sequence) == 0: return False if len(sequence) == 1: return True root = sequence[-1] # 获取根结点 i = 0 while sequence[i] < root: #左子树 i += 1 k = i for i in range(k,len(sequence)): if sequence[i] <= root: #判断右子树 return False left_k = sequence[:k] right_k = sequence[k:len(sequence)-1] left, right = True, True if len(left_k)>0: left = self.VerifySquenceOfBST(left_k) if len(right_k)>0: right = self.VerifySquenceOfBST(right_k) return left and right if __name__ == '__main__': sequence = [4,6,5,9,11,10,8] result = Solution().VerifySquenceOfBST(sequence) print(result)
作者:huangqiancun
出处:http://www.cnblogs.com/huangqiancun/
本博客若无特殊说明则由作者原创发布,欢迎转载,但请注明出处 :)