题目描述
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
题目地址
思路
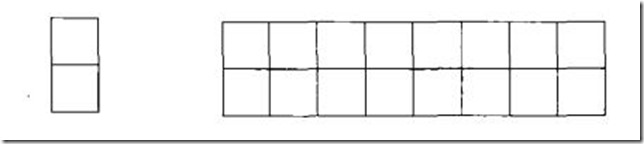
以2x8的矩形为例。示意图如下:
我们先把2x8的覆盖方法记为f(8)。用第一个1x2小矩阵覆盖大矩形的最左边时有两个选择,竖着放或者横着放。当竖着放的时候,右边还剩下2x7的区域,这种情况下的覆盖方法记为f(7)。接下来考虑横着放的情况。当1x2的小矩形横着放在左上角的时候,左下角和横着放一个1x2的小矩形,而在右边还剩下2x6的区域,这种情况下的覆盖方法记为f(6)。因此f(8)=f(7)+f(6)。此时我们可以看出,这仍然是斐波那契数列。
Python
# -*- coding:utf-8 -*- class Solution: def rectCover(self, number): # write code here if number <= 3: return number a, b = 1, 2 for i in range(2,number): c = a+b a,b = b,c return c if __name__ == '__main__': result = Solution().rectCover(4) print(result)
作者:huangqiancun
出处:http://www.cnblogs.com/huangqiancun/
本博客若无特殊说明则由作者原创发布,欢迎转载,但请注明出处 :)