题目描述
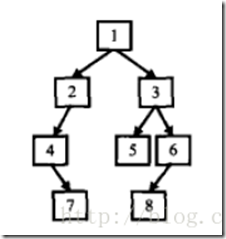
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
题目地址
思路
分解前序遍历序列和后序遍历序列,二叉树的结构如下:
思路:前序遍历先根节点再左子树最后右子树,第一个元素肯定是根节点,然后在中序遍历中寻找根节点的索引,按照中序遍历的规则:先左子树再根节点最后右子树,根节点前的一定是左子树的中序数组,根节点后的一定是右子树的中序数组。
因此,我们每次都需要在前序遍历中找根结点并创建一个根结点,然后在中序遍历中确定根结点位置,并确定当前根结点的左右子树,然后以同样的方法去构建左右子树。这整个过程是一个递归的过程。
Python
# -*- coding:utf-8 -*- class TreeNode: def __init__(self,x): self.val = x self.left = None self.right = None class Solution: # 返回构造的TreeNode根节点 def reConstructBinaryTree(self, pre, tin): # write code here if not pre or not tin or len(pre) != len(tin): return None tree = TreeNode(pre[0]) # for i in range(len(tin)): # if tin[i] == pre[0]: # index = i # break index = tin.index(pre[0]) tree.left = self.reConstructBinaryTree(pre[1:index+1], tin[:index]) tree.right = self.reConstructBinaryTree(pre[index+1:], tin[index+1:]) return tree if __name__ == '__main__': pre = [1,2,4,7,3,5,6,8] tin = [4,7,2,1,5,3,8,6] result = Solution().reConstructBinaryTree(pre,tin)
作者:huangqiancun
出处:http://www.cnblogs.com/huangqiancun/
本博客若无特殊说明则由作者原创发布,欢迎转载,但请注明出处 :)