猜你喜欢推荐系统算法(笔记)
1.现有用户给商品打分的记录如下
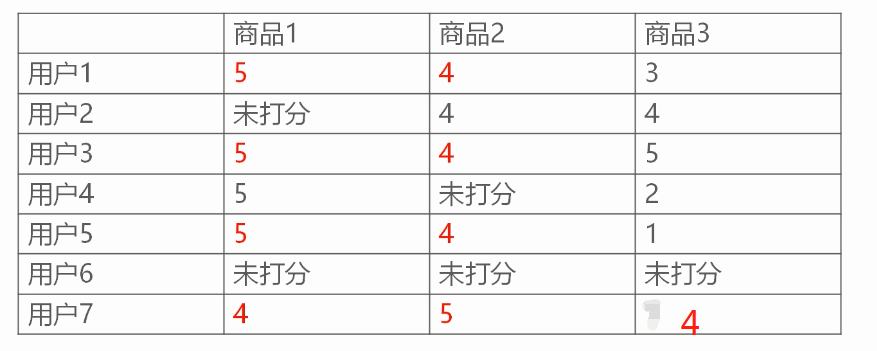
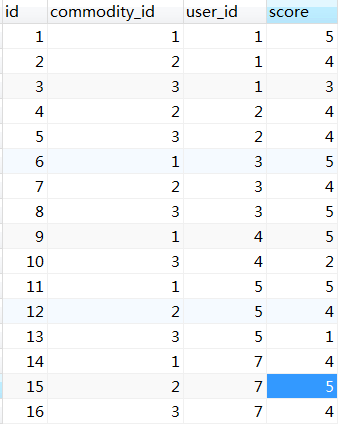
可创建表如图
参考公式: 皮尔逊相关系数
参考地址 : https://segmentfault.com/q/1010000000094674
cov(x,y)=EXY-EX*EY
协方差的定义,EX为随机变量X的数学期望,同理,EXY是XY的数学期望,挺麻烦的,建议你看一下概率论cov(x,y)=EXY-EX*EY
协方差的定义,EX为随机变量X的数学期望,同理,EXY是XY的数学期望,挺麻烦的,建议你看一下概率论
举例:
Xi 1.1 1.9 3
Yi 5.0 10.4 14.6
E(X) = (1.1+1.9+3)/3=2
E(Y) = (5.0+10.4+14.6)/3=10
E(XY)=(1.1×5.0+1.9×10.4+3×14.6)/3=23.02
Cov(X,Y)=E(XY)-E(X)E(Y)=23.02-2×10=3.02
此外:还可以计算:D(X)=E(X^2)-E^2(X)=(1.1^2+1.9^2+3^2)/3 - 4=4.60-4=0.6 σx=0.77
D(Y)=E(Y^2)-E^2(Y)=(5^2+10.4^2+14.6^2)/3-100=15.44 σy=3.93
X,Y的相关系数:
r(X,Y)=Cov(X,Y)/(σxσy)=3.02/(0.77×3.93) = 0.9979
表明这组数据X,Y之间相关性很好!
扩展资料:
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
若两个随机变量X和Y相互独立,则E[(X-E(X))(Y-E(Y))]=0,因而若上述数学期望不为零,则X和Y必不是相互独立的,亦即它们之间存在着一定的关系。
协方差与方差之间有如下关系:
D(X+Y)=D(X)+D(Y)+2Cov(X,Y)
D(X-Y)=D(X)+D(Y)-2Cov(X,Y)
协方差与期望值有如下关系:
Cov(X,Y)=E(XY)-E(X)E(Y)。
协方差的性质:
(1)Cov(X,Y)=Cov(Y,X);
(2)Cov(aX,bY)=abCov(X,Y),(a,b是常数);
(3)Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)。
由协方差定义,可以看出Cov(X,X)=D(X),Cov(Y,Y)=D(Y)。
协方差作为描述X和Y相关程度的量,在同一物理量纲之下有一定的作用,但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念:
定义
称为随机变量X和Y的(Pearson)相关系数。
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
方差是衡量源数据和期望值相差的度量值。
方差在统计描述和概率分布中各有不同的定义,并有不同的公式。
在统计描述中,方差用来计算每一个变量(观察值)与总体均数之间的差异。为避免出现离均差总和为零,离均差平方和受样本含量的影响,统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式:
实际工作中,总体均数难以得到时,应用样本统计量代替总体参数,经校正后,样本方差计算公式:S^2= ∑(X- 
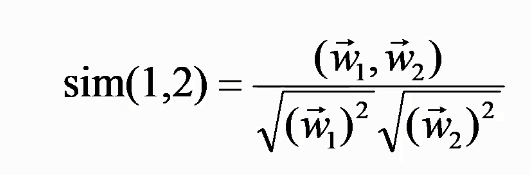
但当数据量小的时候 很容易出现很多接近1的数据 这很明显有问题
这个时候 就需要通过公式减少这种数据的权重
公式如下: sim * 评分人数量 / (1+log(1+人数))
Java 代码 如下 sim为计算出的相关系数
sim = sim * commonItemsLen /(1+ Math.log(1+commonItemsLen));s
使用以上公式虽然降低了人数较少的统计权重 但是又造成了新的问题 会出现大于1 的数
这个时候就需要 进行归一化
//当有多个商品的时候 需要进行归一化
// 商品1 商品2 商品3
//皮尔逊相关系数 //商品1 // 0 0.5 6
//商品2 // 0.5 0 14
//商品3 // 6 14 0
//将得到的值 除以一列的最大值 得到新的推荐值 (这就是归一化)
// 商品1 商品2 商品3
//皮尔逊相关系数 //商品1 // 0 0.5/6 6/6
//商品2 // 0.5/14 0 14/14
//商品3 // 6/14 14/14 0
为用户推荐商品
1. 找到用户喜欢的商品 (本次是使用的用户打分 那么定义为用户 打分大于等于四的是用户喜欢的)
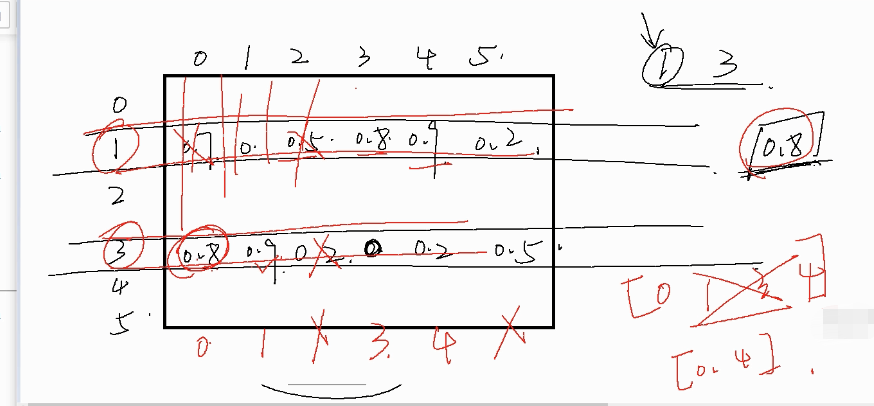
2.假设用户喜欢的是如下图商品index 为1 和3的两个商品 所以找出以下两行数据
3. 定义相似度大于0.8 的给用户推荐 index_1 中能取出 商品3和4 index_3 能取出商品0和1
4.得到集合 [0,1,3,4] 然后因为1和3是用户喜欢过的 所以去掉 给用户推荐[0.4]
召回率: 用户喜欢的(给用户推荐的里面) / 用户喜欢的
准确率: 用户喜欢的(给用户推荐的里面) / 给用户推荐的
两个值存在悖论 : 实际使用中 要适当最好










