回归是数学建模、分类和预测中最古老但功能非常强大的工具之一。回归在工程、物理学、生物学、金融、社会科学等各个领域都有应用,是数据科学家常用的基本工具。
回归通常是机器学习中使用的第一个算法。通过学习因变量和自变量之间的关系实现对数据的预测。例如,对房价估计时,需要确定房屋面积(自变量)与其价格(因变量)之间的关系,可以利用这一关系来预测给定面积的房屋的价格。可以有多个影响因变量的自变量。
因此,回归有两个重要组成部分:自变量和因变量之间的关系,以及不同自变量对因变量影响的强度。
以下是几种常用的回归方法:
- 线性回归:使用最广泛的建模技术之一。已存在 200 多年,已经从几乎所有可能的角度进行了研究。线性回归假定输入变量(X)和单个输出变量(Y)之间呈线性关系。它旨在找到预测值 Y 的线性方程:
其中,X=(x1,x2,...,xn) 为 n 个输入变量,W=(w1,w2,...,wn) 为线性系数,b 是偏置项。目标是找到系数 W 的最佳估计,使得预测值 Y 的误差最小。使用最小二乘法估计线性系数 W,即使预测值 (Yhat) 与观测值 (Y) 之间的差的平方和最小。
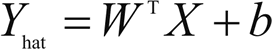
因此,这里尽量最小化损失函数:其中,需要对所有训练样本的误差求和。根据输入变量 X 的数量和类型,可划分出多种线性回归类型:简单线性回归(一个输入变量,一个输出变量),多元线性回归(多个输入变量,一个输出变量),多变量线性回归(多个输入变量,多个输出变量)。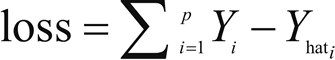
更多线性回归的相关内容,可参考https://en.wikipedia.org/wiki/Linear_regression。
- 逻辑回归:用来确定一个事件的概率。通常来说,事件可被表示为类别因变量。事件的概率用 logit 函数(Sigmoid 函数)表示:
现在的目标是估计权重 W=(w1,w2,...,wn) 和偏置项 b。在逻辑回归中,使用最大似然估计量或随机梯度下降来估计系数。损失函数通常被定义为交叉熵项:
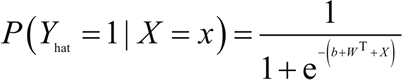
逻辑回归用于分类问题,例如,对于给定的医疗数据,可以使用逻辑回归判断一个人是否患有癌症。如果输出类别变量具有两个或更多个层级,则可以使用多项式逻辑回归。另一种用于两个或更多输出变量的常见技术是 OneVsAll。对于多类型逻辑回归,交叉熵损失函数被修改为: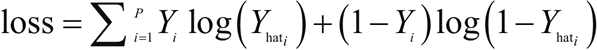
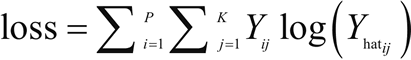
其中,K 是类别总数。更多逻辑回归的相关内容,可参考https://en.wikipedia.org/wiki/Logistic_regression。
- 正则化:当有大量的输入特征时,需要正则化来确保预测模型不会 太复杂。正则化可以帮助防止数据过拟合。它也可以用来获得一个凸损失函数。有两种类型的正则化——L1 和 L2 正则化,其描述如下:
- 当数据高度共线时,L1 正则化也可以工作。在 L1 正则化中,与所有系数的绝对值的和相关的附加惩罚项被添加到损失函数中。L1 正则化的正则化惩罚项如下:
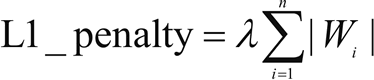
- L2 正则化提供了稀疏的解决方案。当输入特征的数量非常大时,非常有用。在这种情况下,惩罚项是所有系数的平方之和:
其中,λ是正则化参数。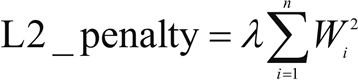
本文来自博客园,作者:大码王,转载请注明原文链接:https://www.cnblogs.com/huanghanyu/

 posted on
posted on

