常用排序与插入算法
冒泡排序
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下:
- 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
冒泡排序的分析
交换过程图示(第一次):
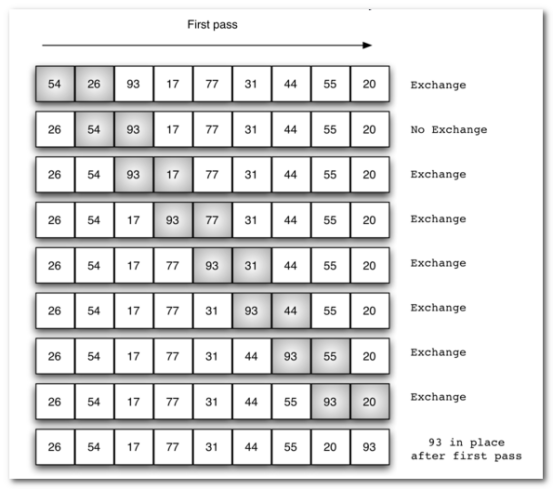
代码如下:
时间复杂度
- 最优时间复杂度:O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
冒泡排序的演示
效果:
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。
选择排序分析
排序过程:
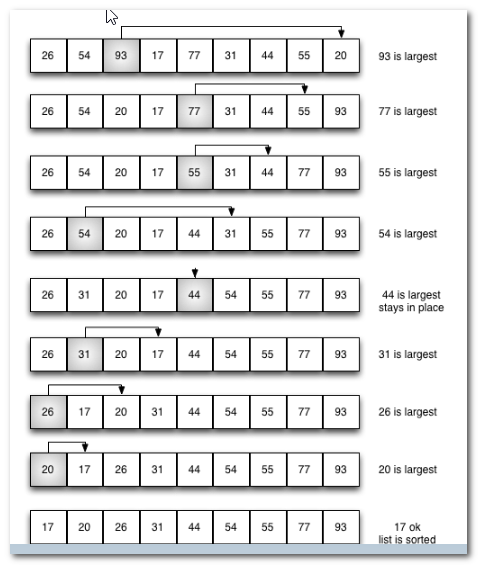
红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置。
def selection_sort(alist): n = len(alist) # 需要进行n-1次选择操作 for i in range(n-1): # 记录最小位置 min_index = i # 从i+1位置到末尾选择出最小数据 for j in range(i+1, n): if alist[j] < alist[min_index]: min_index = j # 如果选择出的数据不在正确位置,进行交换 if min_index != i: alist[i], alist[min_index] = alist[min_index], alist[i] alist = [54,226,93,17,77,31,44,55,20] selection_sort(alist) print(alist)
时间复杂度
- 最优时间复杂度:O(n2)
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定(考虑升序每次选择最大的情况)
选择排序演示
插入排序
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
插入排序分析

时间复杂度
- 最优时间复杂度:O(n) (升序排列,序列已经处于升序状态)
- 最坏时间复杂度:O(n2)
- 稳定性:稳定
插入排序演示
快速排序
快速排序(英语:Quicksort),又称划分交换排序(partition-exchange sort),通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
步骤为:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
快速排序的分析

时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(n2)
- 稳定性:不稳定
从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算,数组的元素都会在每次循环中走访过一次,使用O(n)的时间。在使用结合(concatenation)的版本中,这项运算也是O(n)。
在最好的情况,每次我们运行一次分区,我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此,在到达大小为一的数列前,我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中,不会处理到原来数列的相同部分;因此,程序调用的每一层次结构总共全部仅需要O(n)的时间(每个调用有某些共同的额外耗费,但是因为在每一层次结构仅仅只有O(n)个调用,这些被归纳在O(n)系数中)。结果是这个算法仅需使用O(n log n)时间。
快速排序演示
希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL.Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序过程
希尔排序的基本思想是:将数组列在一个表中并对列分别进行插入排序,重复这过程,不过每次用更长的列(步长更长了,列数更少了)来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身还是使用数组进行排序。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样(竖着的元素是步长组成):
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)
希尔排序的分析
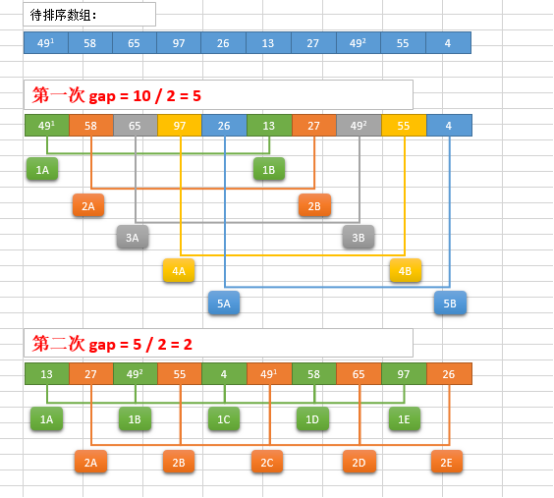
def shell_sort(alist): n = len(alist) # 初始步长 gap = n / 2 while gap > 0: # 按步长进行插入排序 for i in range(gap, n): j = i # 插入排序 while j>=gap and alist[j-gap] > alist[j]: alist[j-gap], alist[j] = alist[j], alist[j-gap] j -= gap # 得到新的步长 gap = gap / 2 alist = [54,26,93,17,77,31,44,55,20] shell_sort(alist) print(alist)
时间复杂度
- 最优时间复杂度:根据步长序列的不同而不同
- 最坏时间复杂度:O(n2)
- 稳定想:不稳定
希尔排序演示
归并排序
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。
将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
归并排序的分析

def merge(li, low, mid, high): i = low j = mid + 1 ltmp = [] while i <= mid and j <= high: if li[i] < li[j]: ltmp.append(li[i]) i += 1 else: ltmp.append(li[j]) j += 1 while i <= mid: ltmp.append(li[i]) i += 1 while j <= high: ltmp.append(li[j]) j += 1 li[low:high+1] = ltmp def _mergesort(li, low, high): if low < high: mid = (low + high) // 2 _mergesort(li,low, mid) _mergesort(li, mid+1, high) merge(li, low, mid, high)
时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(nlogn)
- 稳定性:稳定
堆排序
堆
在这里首先要先解释一下什么是堆,堆栈是计算机的两种最基本的数据结构。堆的特点就是FIFO(first in first out)先进先出,这里的话我觉得可以理解成树的结构。堆在接收数据的时候先接收的数据会被先弹出。
栈的特性正好与堆相反,是属于FILO(first in/last out)先进后出的类型。栈处于一级缓存而堆处于二级缓存中。这个不是本文重点所以不做过多展开。
堆排序节点访问和操作定义
堆节点的访问
在这里我们借用wiki的定义来说明:
通常堆是通过一维数组来实现的。在阵列起始位置为0的情况中
(1)父节点i的左子节点在位置(2*i+1);
(2)父节点i的右子节点在位置(2*i+2);
(3)子节点i的父节点在位置floor((i-1)/2);
堆操作
堆可以分为大根堆和小根堆,这里用最大堆的情况来定义操作:
(1)最大堆调整(MAX_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点。这是核心步骤,在建堆和堆排序都会用到。比较i的根节点和与其所对应i的孩子节点的值。当i根节点的值比左孩子节点的值要小的时候,就把i根节点和左孩子节点所对应的值交换,当i根节点的值比右孩子的节点所对应的值要小的时候,就把i根节点和右孩子节点所对应的值交换。然后再调用堆调整这个过程,可见这是一个递归的过程。
(2)建立最大堆(Build_Max_Heap):将堆所有数据重新排序。建堆的过程其实就是不断做最大堆调整的过程,从len/2出开始调整,一直比到第一个节点。
(3)堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算。堆排序是利用建堆和堆调整来进行的。首先先建堆,然后将堆的根节点选出与最后一个节点进行交换,然后将前面len-1个节点继续做堆调整的过程。直到将所有的节点取出,对于n个数我们只需要做n-1次操作。
这里用网上的一张直观图来感受一下
def sift(data, low, high): i = low j = 2 * i + 1 tmp = data[i] while j <= high: #只要没到子树的最后 if j+1 <= high and data[j] < data[j + 1]: #如果有右孩子且比左孩子大 j += 1 #就把j指向右孩子 if tmp < data[j]:#如果领导不能干 data[i] = data[j] #小领导上位 i = j j = 2 * i + 1 else: break data[i] = tmp def heap_sort(data): n = len(data) for i in range(n // 2 - 1, -1, -1): sift(data, i, n - 1) for i in range(n - 1, -1, -1): data[0], data[i] = data[i], data[0] sift(data, 0, i - 1)
查找算法
搜索是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的,因为该项目是否存在。 搜索的几种常见方法:顺序查找、二分法查找、二叉树查找、哈希查找
二分法查找
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
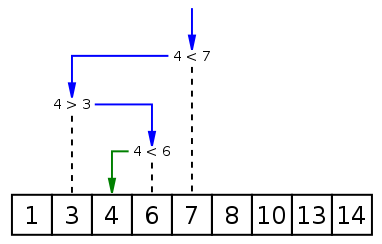
二分法查找实现
(非递归实现)
def binary_search(alist, item): first = 0 last = len(alist)-1 while first<=last: midpoint = (first + last)/2 if alist[midpoint] == item: return True elif item < alist[midpoint]: last = midpoint-1 else: first = midpoint+1 return False testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,] print(binary_search(testlist, 3)) print(binary_search(testlist, 13)) (递归实现) def binary_search(alist, item): if len(alist) == 0: return False else: midpoint = len(alist)//2 if alist[midpoint]==item: return True else: if item<alist[midpoint]: return binary_search(alist[:midpoint],item) else: return binary_search(alist[midpoint+1:],item) testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,] print(binary_search(testlist, 3)) print(binary_search(testlist, 13))
时间复杂度
- 最优时间复杂度:O(1)
- 最坏时间复杂度:O(logn)
python
算法时间复杂度总结
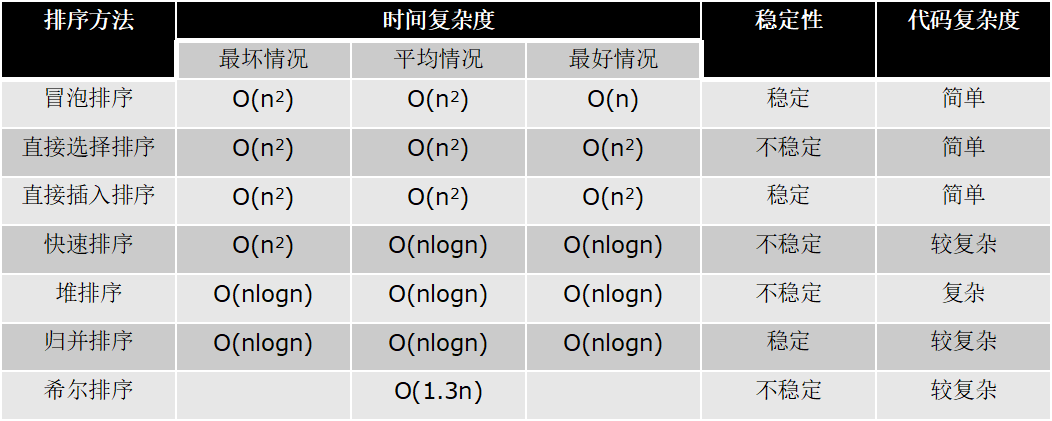
本文来自博客园,作者:大码王,转载请注明原文链接:https://www.cnblogs.com/huanghanyu/



 posted on
posted on













【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具