
一、线性回归的概念
1.1、定义
线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。
优点:
结果易于理解,计算不复杂。
缺点:
对非线性的数据拟合不好。
适用数据类型:
数值型和标称型。
1.2、分类
一元线性回归:
涉及到的变量只有一个。
多元线性回归:
涉及到的变量两个或两个以上。
1.3、公式

其中𝑤,𝑥为矩阵:

二、线性回归的实例
2.1、单变量实例
房子价格与房子面积

2.2、多变量实例
期末成绩:0.7×考试成绩+0.3×平时成绩
西瓜好坏:0.2×色泽+0.5×根蒂+0.3×敲声

三、损失函数
损失函数是一个贯穿整个机器学习重要的一个概念,大部分机器学习算法都会有误差,我们得通过显性的公式来描述这个误差,并且将这个误差优化到最小值。
3.1、损失原因
预测结果与真实值是有一定的误差。

3.2、损失函数定义
损失函数代表了误差的大小,用公式表示如下:

又称最小二乘法。
对于线性回归模型,将模型与数据点之间的距离差之和做为衡量匹配好坏的标准,误差越小,匹配程度越大。我们要找的模型就是需要将f(x)和我们的真实值之间最相似的状态。
损失函数由W决定,那么如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)

3.3、减小损失函数的2种方式
方式一:最小二乘法之正规方程
求解:

𝑋为特征值矩阵,𝑦为目标值矩阵。

缺点:当特征过于复杂,求解速度太慢。
对于复杂的算法,不能使用正规方程求解(逻辑回归等)
方式二:最小二乘法之梯度下降

𝛼为学习速率,需要手动指定,其中

表示方向
理解:沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后
更新W值


3.4、两种方式对比:

四、线性回归API
4.1、普通最小二乘法线性回归
sklearn.linear_model.LinearRegression()
coef_:回归系数
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
# 方法
reg.fit(X,y,sample_weight = None) #使用X作为训练数据拟合模型,y作为X的类别值。X,y为数组或者矩阵
reg.predict([[X,y]]) # 预测提供的数据对应的结果
#属性
reg.coef_ #表示回归系数w=(w1,w2....)
4.2、通过使用SGD最小线性模型
sklearn.linear_model.SGDRegressor( )
coef_:回归系数
4.3、带有正则化的线性回归
sklearn.linear_model.Ridge
具有l2正则化的线性最小二乘法
alpha:正则化力度
coef_:回归系数
五、实现案例
波士顿房价数据分析流程:
5.1、数据获取
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, classification_report
from sklearn.externals import joblib
import pandas as pd
import numpy as np
# 获取数据
lb = load_boston()
5.2、数据分割
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
5.3、训练与测试数据标准化处理
# 特征值和目标值是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train)
y_test = std_y.transform(y_test)
5.4、线性回归模型和梯度下降估计对房价进行预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_)
保存训练好的模型
joblib.dump(lr, "test.pkl")
# 预测测试集的房子价格
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("正规方程测试集里面每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
# 梯度下降进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print(sgd.coef_)
# 预测测试集的房子价格
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print("梯度下降测试集里面每个房子的预测价格:", y_sgd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
# 岭回归进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print(rd.coef_)
# 预测测试集的房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
print("梯度下降测试集里面每个房子的预测价格:", y_rd_predict)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
六、回归的性能评估
6.1、均方差误差评估机制 (MSE):

注:𝑦^𝑖为预测值,¯𝑦为真实值。
6.2、回归评估API:
sklearn.metrics.mean_squared_error
mean_squared_error(y_true, y_pred)
均方误差回归损失
y_true:真实值
y_pred:预测值
return:浮点数结果
注:真实值,预测值为标准化之前的值。
七、线性回归的可能问题
训练数据训练的很好啊,误差也不大,为什么在测试集上面有问题呢?机器学习可能存在过拟合和欠拟合的问题。如下图:


7.1、过拟合
一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂),如下图:

产生原因:
原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点。
解决办法:
- 进行特征选择,消除关联性大的特征(很难做)
- 交叉验证(建议使用)
- 正则化 (了解即可)
7.2、欠拟合
一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)。如下图:

产生原因:
学习到数据的特征过少。
解决办法:
增加数据的特征数量。
1、问题引入
在统计学中,线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。一个带有一个自变量的线性回归方程代表一条直线。我们需要对线性回归结果进行统计分析。
例如,假设我们已知一些学生年纪和游戏时间的数据,可以建立一个回归方程,输入一个新的年纪时,预测该学生的游戏时间。自变量为学生年纪,因变量为游戏时间。当只有一个因变量时,我们称该类问题为简单线性回归。当游戏时间与学生年纪和学生性别有关,因变量有多个时,我们称该类问题为多元线性回归。
2、常见的统计量
在研究该问题之前,首先了解下编程中用到的常见的统计量:
|
序号 |
概念 |
公式 |
算法 |
说明 |
|
1 |
均值 |
|
整体的均值 |
|
|
2 |
中位数 |
|
排序后取中间值 |
|
|
3 |
众数 |
|
出现次数最多的数 |
出现频率 |
|
4 |
方差 |
|
数据的离散程度 |
|
|
5 |
标准差 |
|
s |
方差的开方 |
2、简单线性回归实例及编程实现
研究一个自变量(X)和一个因变量(y)的关系
简单线性回归模型定义:

简单线性回归方程:
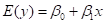
其中:
 为回归线的截距
为回归线的截距
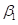 为回归线的斜率
为回归线的斜率
通过训练数据,求取出估计参数建立的直线方程:
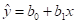
实际编程时,主要是根据已知训练数据,估计出 和
和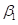 的值
的值 和
和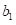
以下面实例为例,第一列表示每月投放广告的次数,第二列表示汽车向量,通过Python编程求取线性回归方程:
|
投放广告数 |
汽车销量 |
|
1 |
14 |
|
3 |
24 |
|
2 |
18 |
|
1 |
17 |
|
3 |
27 |
编程关键在于如何求取b0和b1的值,我们引入一个方程(sum of square):
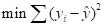
当上述方程的值最小时,我们认为求取到线程回归方程参数的值,对该方程求最小值可以进一步转化为求导和求极值的问题,求导过程省略,最后结论如下:
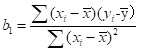
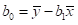
实际代码:
import numpy as np from matplotlib import pylab as pl # 定义训练数据 x = np.array([1,3,2,1,3]) y = np.array([14,24,18,17,27]) # 回归方程求取函数 def fit(x,y): if len(x) != len(y): return numerator = 0.0 denominator = 0.0 x_mean = np.mean(x) y_mean = np.mean(y) for i in range(len(x)): numerator += (x[i]-x_mean)*(y[i]-y_mean) denominator += np.square((x[i]-x_mean)) print('numerator:',numerator,'denominator:',denominator) b0 = numerator/denominator b1 = y_mean - b0*x_mean return b0,b1 # 定义预测函数 def predit(x,b0,b1): return b0*x + b1 # 求取回归方程 b0,b1 = fit(x,y) print('Line is:y = %2.0fx + %2.0f'%(b0,b1)) # 预测 x_test = np.array([0.5,1.5,2.5,3,4]) y_test = np.zeros((1,len(x_test))) for i in range(len(x_test)): y_test[0][i] = predit(x_test[i],b0,b1) # 绘制图像 xx = np.linspace(0, 5) yy = b0*xx + b1 pl.plot(xx,yy,'k-') pl.scatter(x,y,cmap=pl.cm.Paired) pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired) pl.show()
执行结果:
C:\Anaconda3\python.exe "C:\Program Files\JetBrains\PyCharm 2019.1.1\helpers\pydev\pydevconsole.py" --mode=client --port=51452 import sys; print('Python %s on %s' % (sys.version, sys.platform)) sys.path.extend(['C:\\app\\PycharmProjects', 'C:/app/PycharmProjects']) Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] Type 'copyright', 'credits' or 'license' for more information IPython 7.12.0 -- An enhanced Interactive Python. Type '?' for help. PyDev console: using IPython 7.12.0 Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] on win32 runfile('C:/app/PycharmProjects/ArtificialIntelligence/test.py', wdir='C:/app/PycharmProjects/ArtificialIntelligence') numerator: 20.0 denominator: 4.0 Line is:y = 5x + 10
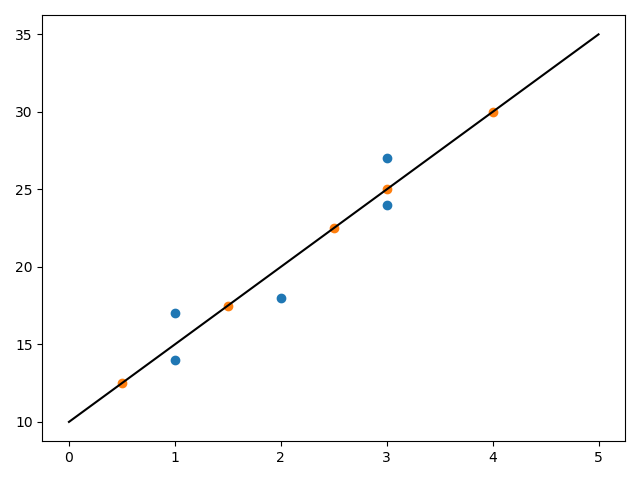
蓝色表示测试数据,橙色表示预测数据。
3、多元线性回归实例及编程实现
多元线性回归方程和简单线性回归方程类似,不同的是由于因变量个数的增加,求取参数的个数也相应增加,推导和求取过程也不一样。
y=β0+β1x1+β2x2+ ... +βpxp+ε
对于b0、b1、…、bn的推导和求取过程,引用一个第三方库进行计算。以如下数据为例,对运输里程、运输次数与运输总时间的关系,建立多元线性回归模型:
|
运输里程 |
运输次数 |
运输总时间 |
|
100 |
4 |
9.3 |
|
50 |
3 |
4.8 |
|
100 |
4 |
8.9 |
|
100 |
2 |
6.5 |
|
50 |
2 |
4.2 |
|
80 |
2 |
6.2 |
|
75 |
3 |
7.4 |
|
65 |
4 |
6.0 |
|
90 |
3 |
7.6 |
|
90 |
2 |
6.1 |
代码如下:
import numpy as np from sklearn import datasets,linear_model # 定义训练数据 x = np.array([[100,4,9.3],[50,3,4.8],[100,4,8.9], [100,2,6.5],[50,2,4.2],[80,2,6.2], [75,3,7.4],[65,4,6],[90,3,7.6],[90,2,6.1]]) print(x) X = x[:,:-1] Y = x[:,-1] print(X,Y) # 训练数据 regr = linear_model.LinearRegression() regr.fit(X,Y) print('coefficients(b1,b2...):',regr.coef_) print('intercept(b0):',regr.intercept_) # 预测 x_test = np.array([[102,6],[100,4]]) y_test = regr.predict(x_test) print(y_test)
执行结果:
C:\Anaconda3\python.exe "C:\Program Files\JetBrains\PyCharm 2019.1.1\helpers\pydev\pydevconsole.py" --mode=client --port=51529 import sys; print('Python %s on %s' % (sys.version, sys.platform)) sys.path.extend(['C:\\app\\PycharmProjects', 'C:/app/PycharmProjects']) Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] Type 'copyright', 'credits' or 'license' for more information IPython 7.12.0 -- An enhanced Interactive Python. Type '?' for help. PyDev console: using IPython 7.12.0 Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] on win32 runfile('C:/app/PycharmProjects/ArtificialIntelligence/test.py', wdir='C:/app/PycharmProjects/ArtificialIntelligence') [[100. 4. 9.3] [ 50. 3. 4.8] [100. 4. 8.9] [100. 2. 6.5] [ 50. 2. 4.2] [ 80. 2. 6.2] [ 75. 3. 7.4] [ 65. 4. 6. ] [ 90. 3. 7.6] [ 90. 2. 6.1]] [[100. 4.] [ 50. 3.] [100. 4.] [100. 2.] [ 50. 2.] [ 80. 2.] [ 75. 3.] [ 65. 4.] [ 90. 3.] [ 90. 2.]] [9.3 4.8 8.9 6.5 4.2 6.2 7.4 6. 7.6 6.1] coefficients(b1,b2...): [0.0611346 0.92342537] intercept(b0): -0.868701466781709 [10.90757981 8.93845988]
如果特征向量中存在分类型变量,例如车型,我们需要进行特殊处理:
|
运输里程 |
输出次数 |
车型 |
隐式转换 |
运输总时间 |
|
100 |
4 |
1 |
010 |
9.3 |
|
50 |
3 |
0 |
100 |
4.8 |
|
100 |
4 |
1 |
010 |
8.9 |
|
100 |
2 |
2 |
001 |
6.5 |
|
50 |
2 |
2 |
001 |
4.2 |
|
80 |
2 |
1 |
010 |
6.2 |
|
75 |
3 |
1 |
010 |
7.4 |
|
65 |
4 |
0 |
100 |
6.0 |
|
90 |
3 |
0 |
100 |
7.6 |
|
100 |
4 |
1 |
010 |
9.3 |
|
50 |
3 |
0 |
100 |
4.8 |
|
100 |
4 |
1 |
010 |
8.9 |
|
100 |
2 |
2 |
001 |
6.5
|
代码实现:
import numpy as np from sklearn.feature_extraction import DictVectorizer from sklearn import linear_model # 定义数据集 x = np.array([[100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9], [100,2,2,6.5],[50,2,2,4.2],[80,2,1,6.2], [75,3,1,7.4],[65,4,0,6],[90,3,0,7.6], [100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9],[100,2,2,6.5]]) x_trans = [] for i in range(len(x)): x_trans.append({'x1':str(x[i][2])}) vec = DictVectorizer() dummyX = vec.fit_transform(x_trans).toarray() x = np.concatenate((x[:,:-2],dummyX[:,:],x[:,-1].reshape(len(x),1)),axis=1) x = x.astype(float) X = x[:,:-1] Y = x[:,-1] print(x,X,Y) # 训练数据 regr = linear_model.LinearRegression() regr.fit(X,Y) print('coefficients(b1,b2...):',regr.coef_) print('intercept(b0):',regr.intercept_)
执行结果:
C:\Anaconda3\python.exe "C:\Program Files\JetBrains\PyCharm 2019.1.1\helpers\pydev\pydevconsole.py" --mode=client --port=51576 import sys; print('Python %s on %s' % (sys.version, sys.platform)) sys.path.extend(['C:\\app\\PycharmProjects', 'C:/app/PycharmProjects']) Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] Type 'copyright', 'credits' or 'license' for more information IPython 7.12.0 -- An enhanced Interactive Python. Type '?' for help. PyDev console: using IPython 7.12.0 Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] on win32 runfile('C:/app/PycharmProjects/ArtificialIntelligence/test.py', wdir='C:/app/PycharmProjects/ArtificialIntelligence') [[100. 4. 0. 1. 0. 9.3] [ 50. 3. 1. 0. 0. 4.8] [100. 4. 0. 1. 0. 8.9] [100. 2. 0. 0. 1. 6.5] [ 50. 2. 0. 0. 1. 4.2] [ 80. 2. 0. 1. 0. 6.2] [ 75. 3. 0. 1. 0. 7.4] [ 65. 4. 1. 0. 0. 6. ] [ 90. 3. 1. 0. 0. 7.6] [100. 4. 0. 1. 0. 9.3] [ 50. 3. 1. 0. 0. 4.8] [100. 4. 0. 1. 0. 8.9] [100. 2. 0. 0. 1. 6.5]] [[100. 4. 0. 1. 0.] [ 50. 3. 1. 0. 0.] [100. 4. 0. 1. 0.] [100. 2. 0. 0. 1.] [ 50. 2. 0. 0. 1.] [ 80. 2. 0. 1. 0.] [ 75. 3. 0. 1. 0.] [ 65. 4. 1. 0. 0.] [ 90. 3. 1. 0. 0.] [100. 4. 0. 1. 0.] [ 50. 3. 1. 0. 0.] [100. 4. 0. 1. 0.] [100. 2. 0. 0. 1.]] [9.3 4.8 8.9 6.5 4.2 6.2 7.4 6. 7.6 9.3 4.8 8.9 6.5] coefficients(b1,b2...): [ 0.05452507 0.70930079 -0.18019642 0.60821607 -0.42801964] intercept(b0): 0.1989958956317821
本文来自博客园,作者:大码王,转载请注明原文链接:https://www.cnblogs.com/huanghanyu/

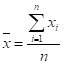
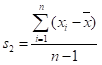
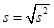


 posted on
posted on













【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具