8.递归
如何理解“递归”
比如在电影院不知道自己现在坐的位置是第几排,就问下前排的是第几排(x),自己就是x+1,如果他也不知道他就继续问前排,知道问道第一排的人,这是“递”。
而第一排的人往会一排排传自己是第几排,这就是“归”。
递推公式就是如下:
f(n)=f(n-1)+1 其中,f(1)=1
改成代码:
1 int f(int n) { 2 if (n == 1) return 1; 3 return f(n-1) + 1; 4 }
递归需要满足的三个条件:
1.一个问题的解可以分解为几个子问题的解
子问题就是数据规模更小的问题。刚才的例中,“自己在哪一排”可以分解为“前一排的人在哪一排”
2.这个问题与分解者之后的子问题,除了数据规模不同,求解思路完全一样
3.存在递归终止条件
如何编写递归代码?
关键是找出递归公式,找到终止条件。
假设有n个台阶,每次可以走1个台阶或者2个台阶,那么有多少种走法?
根据第一步的走法可以把所有走法分为两类,1.是第一步走1个台阶(接下来有f(n-1)种),2.是第一步走2个台阶(接下来有f(n-2)种)。所以用公式表达:
f(n) = f(n -1) + f(n - 2)
接下来就是终止条件,显然是需要f(1) = 1,f(2) = 2
递推公式:
f(1) = 1;
f(2) = 2;
f(n) = f(n-1)+f(n-2)
因此代码就是:
1 int f(int n) { 2 if (n == 1) return 1; 3 if (n == 2) return 2; 4 return f(n-1) + f(n-2); 5 }
当我们看到递归时,总想着把递归平铺展开,脑子里就会循环,一层一层往下调,然后再一层一层返回,试图想该清楚计算机每一步都是怎么执行的,这样就就很容易被绕进去。这种试图想清楚整个递和归过程的作法,实际上是进入了一个思维误区。
正确的思维是如果一个问题A可以分解为若干个子问题B,C,D,你可以假设B,C,D已经解决,在此基础上思考如何解决问题A。
计算机擅长做重复的事情,递归正和他胃口。
递归代买要警惕堆栈溢出
函数调用会使用栈来保存临时变量,每调用一个函数,都会将临时变量封装为栈帧压入内存栈,等函数执行完成返回时,才出栈。系统栈挥着虚拟机栈空间一般都不大,如果数据规模很大,调用层次很深,一致压入栈,就会 有堆栈溢出的风险。
例如电影院例子,我们将系统栈或者JVM堆栈大小设置为1KB,在求解f(19999)时就会报错:
Exception in thread "main" java.lang.StackOverflowError
可以设置递归调用深度的方式来解决这个问题,如电影院例子
1 // 全局变量,表示递归的深度。 2 int depth = 0; 3 4 int f(int n) { 5 ++depth; 6 if (depth > 1000) throw exception; 7 8 if (n == 1) return 1; 9 return f(n-1) + 1; 10 }
但这个方法却不实用,因为最大允许的递归深度和当前线程剩余的栈空间大小有关,实时计算的话代码太复杂。
递归代码要警惕重复计算
如上面的计算台阶数问题,递归图会如下:
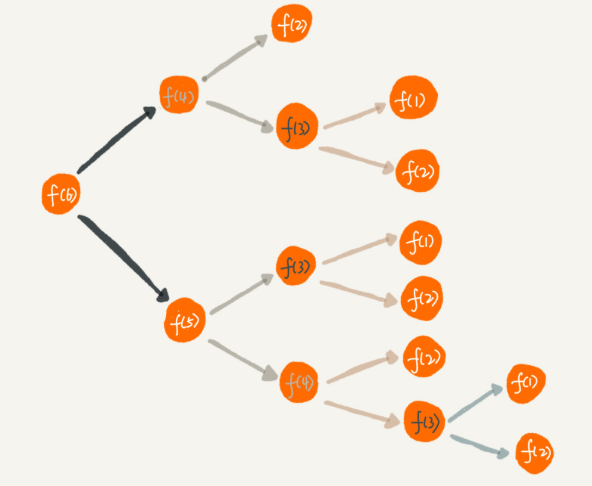
f(3)就被重复计算了。
避免重复计算,可以通过一个数据结构(比如散列表)来保存已经求解过的f(k)。当递归调用到f(k),先看下是否已经求解过了。
改造后代码:
1 public int f(int n) { 2 if (n == 1) return 1; 3 if (n == 2) return 2; 4 5 // hasSolvedList 可以理解成一个 Map,key 是 n,value 是 f(n) 6 if (hasSolvedList.containsKey(n)) { 7 return hasSovledList.get(n); 8 } 9 10 int ret = f(n-1) + f(n-2); 11 hasSovledList.put(n, ret); 12 return ret; 13 } 14
递归代码除了堆栈溢出、重复计算这两个问题外,当函数调用量特别大时,会积聚成一个可观的时间成本,另外它的空间复杂度上也需要考虑,电影院的空间复杂度O(n),而不是O(1)
怎么将递归代码改写成非递归代码?
递归有利有弊,表达力强,代码简洁,但却存在上面的问题。
抛开电影院场景,只看f(x) = f(x - 1) + 1,f(1) = 1,这个递归公式,可以改写成:
1 int f(int n) { 2 int ret = 1; 3 for (int i = 2; i <= n; ++i) { 4 ret = ret + 1; 5 } 6 return ret; 7 }
同样台阶例子:
1 int f(int n) { 2 if (n == 1) return 1; 3 if (n == 2) return 2; 4 5 int ret = 0; 6 int pre = 2; 7 int prepre = 1; 8 for (int i = 3; i <= n; ++i) { 9 ret = pre + prepre; #n台阶走的数 = (n-1)台阶的步数 + (n-2)的台阶步数 10 prepre = pre; 11 pre = ret; 12 } 13 return ret; 14 }
那么是不是所有的递归代买都可以改为这种迭代循环的非递归写法呢?
是的。递归本身就是借助栈实现的,只不过那是系统或者虚拟机本身提供的,我们没有感知。如果我们在内存堆上实现栈,手动模拟入栈、出栈过程,那任何递归代码都可以改成不像递归代码的样子。
但这种思路只是改成了“手动”,本质没变,上述递归的问题仍存在。

